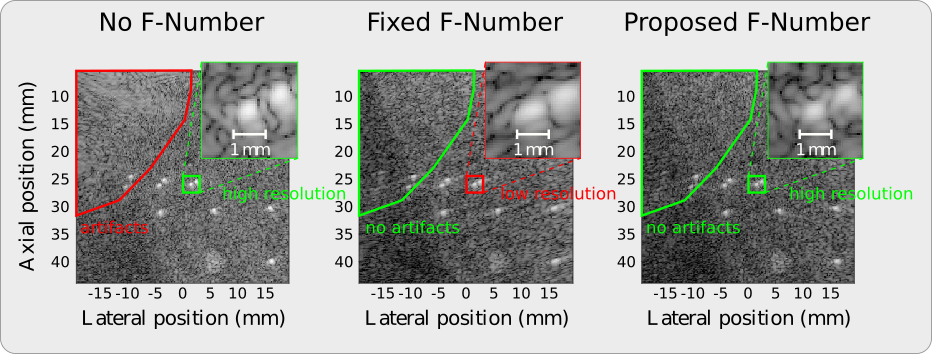
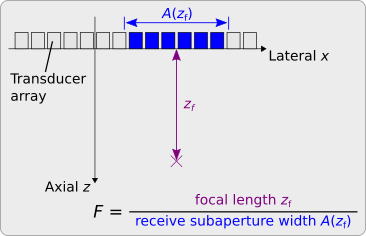
Frequency-Dependent F-Number for Coherent Plane-Wave Compounding

Simple MATLAB and CUDA implementations of the frequency-dependent F-number [1], [2] for coherent plane-wave compounding.

What is an F-Number?

The F-number is a user-defined parameter of a technique known as "dynamic receive aperture". Such apertures reduce image artifacts in all image formation methods using the delay-and-sum (DAS) algorithm, such as

coherent plane-wave compounding [3], or
synthetic aperture imaging [4].

The receive aperture widens with the focal length. The F-number, for a uniform linear transducer array, equals the quotient of the focal length and the width of the receive subaperture.

The usage of a fixed F-number results in a dynamic receive subaperture whose width increases with the focal length.

Established Methods to Compute the F-Number are Contradictory and Yield Frequency-Dependent Results

Established methods to compute the optimal F-number attribute the image artifacts to two different phenomena:

Noise [5], [6], [3]: The directivity of the array elements attenuates the echoes and reduces the signal-to-noise ratio of the recorded signals.
Grating lobes [7], [8]: The width of the receive subaperture determines the grating lobe-to-main lobe ratio.

Both approaches, although yielding similar F-numbers (0.5 <= F <= 2), are mutually contradictory.

Wide array elements, for example, show an increased directivity.
The "Noise" approach suggests the usage of narrow receive subapertures or, equivalently, large F-numbers for such elements to improve the signal-to-noise ratio.
The "Grating lobes" approach, in contrast, permits wide receive subapertures or, equivalently, small F-numbers for such elements because they attenuate the grating lobes.

Both approaches, moreover, yield F-numbers that increase with the frequency.

The DAS algorithm, however, requires a fixed F-number and typically uses the maximum F-number at the upper frequency bound. This F-number satifies the conditions for all lower frequencies but, owing to its suboptimal value, reduces the spatial resolution.

What Does the Proposed F-Number Accomplish?

The proposed F-number not only eliminates image artifacts but also maintains the spatial resolution of the full aperture [1], [2].

This F-number, in particular, prevents the first-order grating lobes from insonifying reflective image structures. The F-number, to this end, uses a closed-form expression, which derives from the far-field sensitivity of the focused receive subaperture, to impose a minimum angular distance on these grating lobes.

How Does the Implementation Work?

A Fourier-domain beamforming algorithm enables the usage of frequency-dependent F-numbers. The algorithm not only varies the width of the receive subaperture with the voxel position but also with the frequency. This additional frequency dependence, in contrast to a fixed F-number, includes additional frequency components that improve both the contrast and the spatial resolution.

Method	Width of the receive subaperture	Spatial resolution	Grating lobe suppression
No F-number	always full	optimal	none
Fixed F-number	position-dependent	minimal	exaggerated
Proposed F-number	frequency- and position-dependent	almost optimal	optimal

Getting Started

Clone the repository or download the release to your local hard drive.

git clone https://github.com/mschiffn/f_number

Add the repository to your MATLAB path.

addpath( genpath( './f_number' ) )

Run the script "examples.m".

examples

Folder Structure

The repository has the following structure:

.
├── +auxiliary      # auxiliary functions (e.g., dimension and size check)
├── +cuda           # C++/CUDA implementation and MEX interface
├── +f_numbers      # classes for various types of F-numbers (e.g., constant, directivity-derived, proposed)
├── +normalizations # classes for various types of normalizations (e.g., off, on, window-based)
├── +platforms      # classes for various types of platforms (e.g., CPU, GPU)
├── +windows        # classes for various window functions (e.g., boxcar, Hann, Tukey)
├── das_pw.m        # main function
├── data_RF.mat     # experimental data (tissue phantom)
├── examples.m      # examples for the usage of the main function
├── LICENSE         # license file
└── README.md       # this readme

The packages +f_numbers, +normalizations, and +windows contain exemplary class hierarchies to manage various types of F-numbers, normalizations, and window functions.

Image Formation

Use the function das_pw to form images.

In MATLAB type

help das_pw

to obtain an explanation of the input and output arguments.

The typical usage is:

[ image, F_number_values ] = das_pw( positions_x, positions_z, data_RF, f_s, theta_incident, element_width, element_pitch, [ f_lb, f_ub ], c_ref, N_samples_shift, window, F_number, normalization, platform );

The proposed F-number can be instantiated by

chi_lb = 45;  % minimum angular distance of the first-order grating lobes (°)
F_ub = 3;     % maximum permissible F-number
delta = 10;   % safety margin for anti-lobe aliasing (°)
F_number_rx = f_numbers.grating.angle_lb( chi_lb, F_ub, delta );

The directivity-derived F-numbers [5], [6] are

width_over_pitch = 0.918;  % element width-to-element pitch ratio (1)
F_number_rx_1 = f_numbers.directivity.perrot( width_over_pitch );
F_number_rx_2 = f_numbers.directivity.szabo( width_over_pitch );

The standard fixed F-number is

F_number_rx_3 = f_numbers.constant( 3 );

The MEX interface to the C++/CUDA implementation must be compiled:

mexcuda '-L/usr/local/cuda/lib64' -lcudart -lcufft gpu_bf_das_pw_rf.cu

You might have to adapt the library path (here: /usr/local/cuda/lib64) to your system.

📓 References

M. F. Schiffner and G. Schmitz, "Frequency-dependent F-number suppresses grating lobes and improves the lateral resolution in coherent plane-wave compounding," IEEE Trans. Ultrason., Ferroelectr., Freq. Control (2023).
M. F. Schiffner and G. Schmitz, "Frequency-dependent F-number increases the contrast and the spatial resolution in fast pulse-echo ultrasound imaging," 2021 IEEE Int. Ultrasonics Symp. (IUS), Xi’an, China, Sep. 2021, pp. 1–4.
G. Montaldo, M. Tanter, J. Bercoff, N. Benech, and M. Fink, “Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography," IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 56, no. 3, pp. 489–506, Mar. 2009.
J. A. Jensen, S. I. Nikolov, K. L. Gammelmark, and M. H. Pedersen, “Synthetic aperture ultrasound imaging,” Ultrasonics, vol. 44, Supplement, e5–e15, Dec. 2006.
V. Perrot, M. Polichetti, F. Varray, and D. Garcia, “So you think you can DAS? A viewpoint on delay-and-sum beamforming,” Ultrasonics, vol. 111, p. 106 309, Mar. 2021.
T. L. Szabo, Diagnostic Ultrasound Imaging: Inside Out, 2nd. Elsevier Academic Press, Dec. 2013
B. Delannoy, R. Torguet, C. Bruneel, E. Bridoux, J. M. Rouvaen, and H. Lasota, “Acoustical image reconstruction in parallel-processing analog electronic systems,” J. Appl. Phys., vol. 50, no. 5, pp. 3153–3159, May 1979.
C. Bruneel, E. Bridoux, B. Delannoy, B. Nongaillard, J. M. Rouvaen, and R. Torguet, “Effect of spatial sampling on an acoustical image reconstruction,” J. Appl. Phys., vol. 49, no. 2, pp. 569–573, Feb. 1978.