This is the Learning Through Target Spikes (LTTS) repository for code associated to the paper: Paolo Muratore, Cristiano Capone, Pier Stanislao Paolucci (2020) "Target spike patterns enable efficient and biologically plausible learning for complex temporal tasks" (published in PlosONE at: https://doi.org/10.1371/journal.pone.0247014).
Please give credit to this paper if you use or modify the code in a derivative work. This work is licensed under the Creative Commons Attribution 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA.
This work is licensed under a Creative Commons Attribution 4.0 International License.
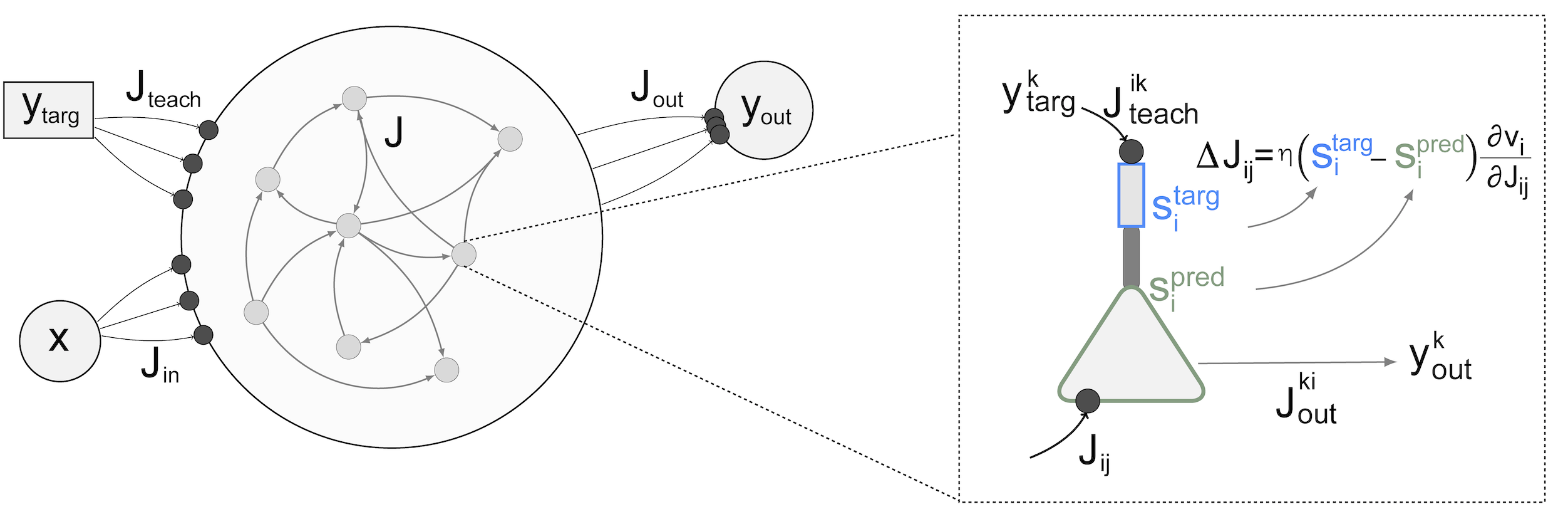
The model is implemented in the ltts.py module. A graphical depiction of the
system architecture is offered in the Figure below.
The code is written in Python 3.7 and for correct execution the program requires
the following external dependences:
numpy
tqdm
To train the model (and save the results as Trained Model.npy) on the standard 3D trajectory task simply run:
python test.py
We test our model on several tasks. See our article for full analysis and descriptions.
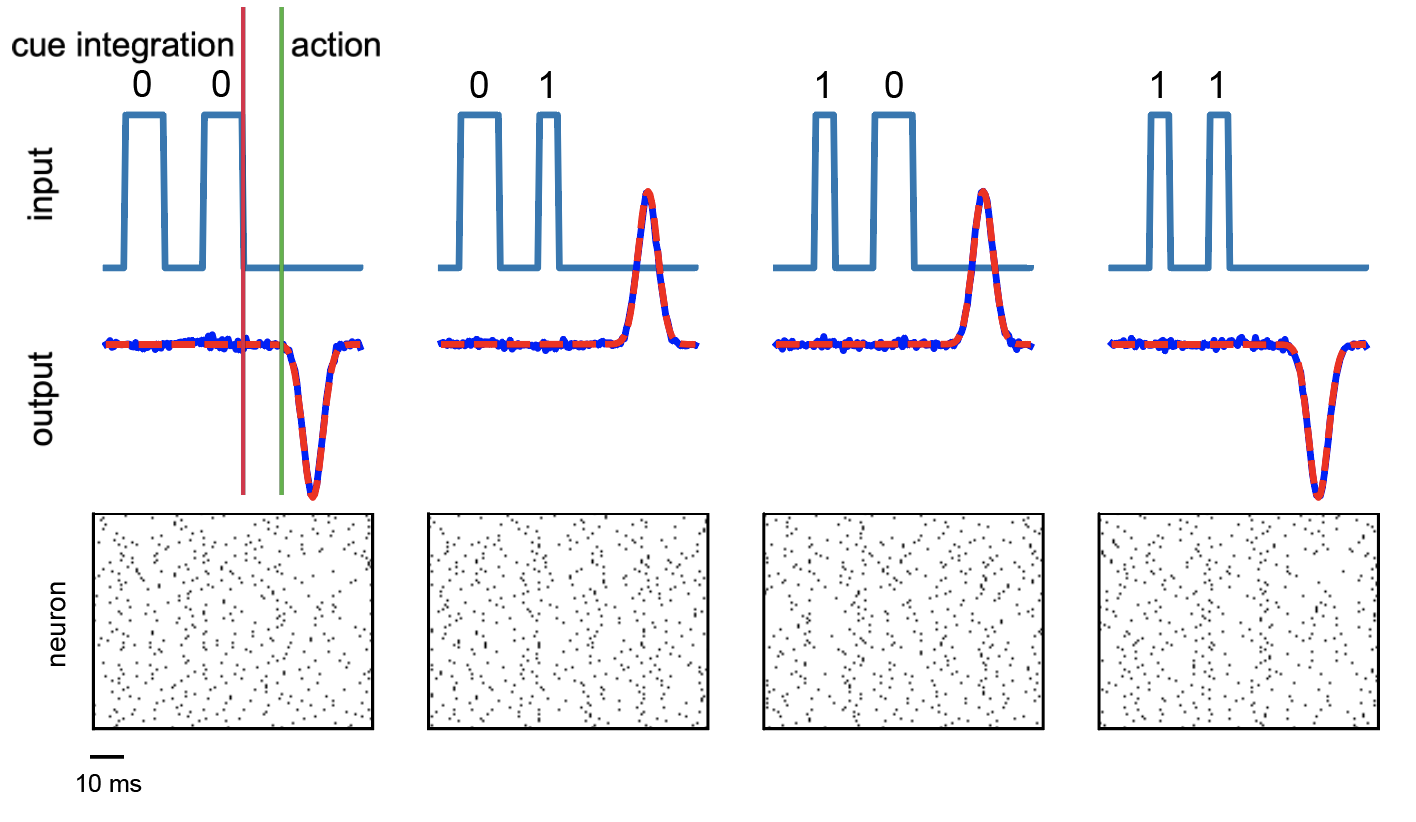
Here we report the results for the temporal XOR, which is a non-linear temporal task in which the network is asked to performed a delayed XOR computation given two inputs.
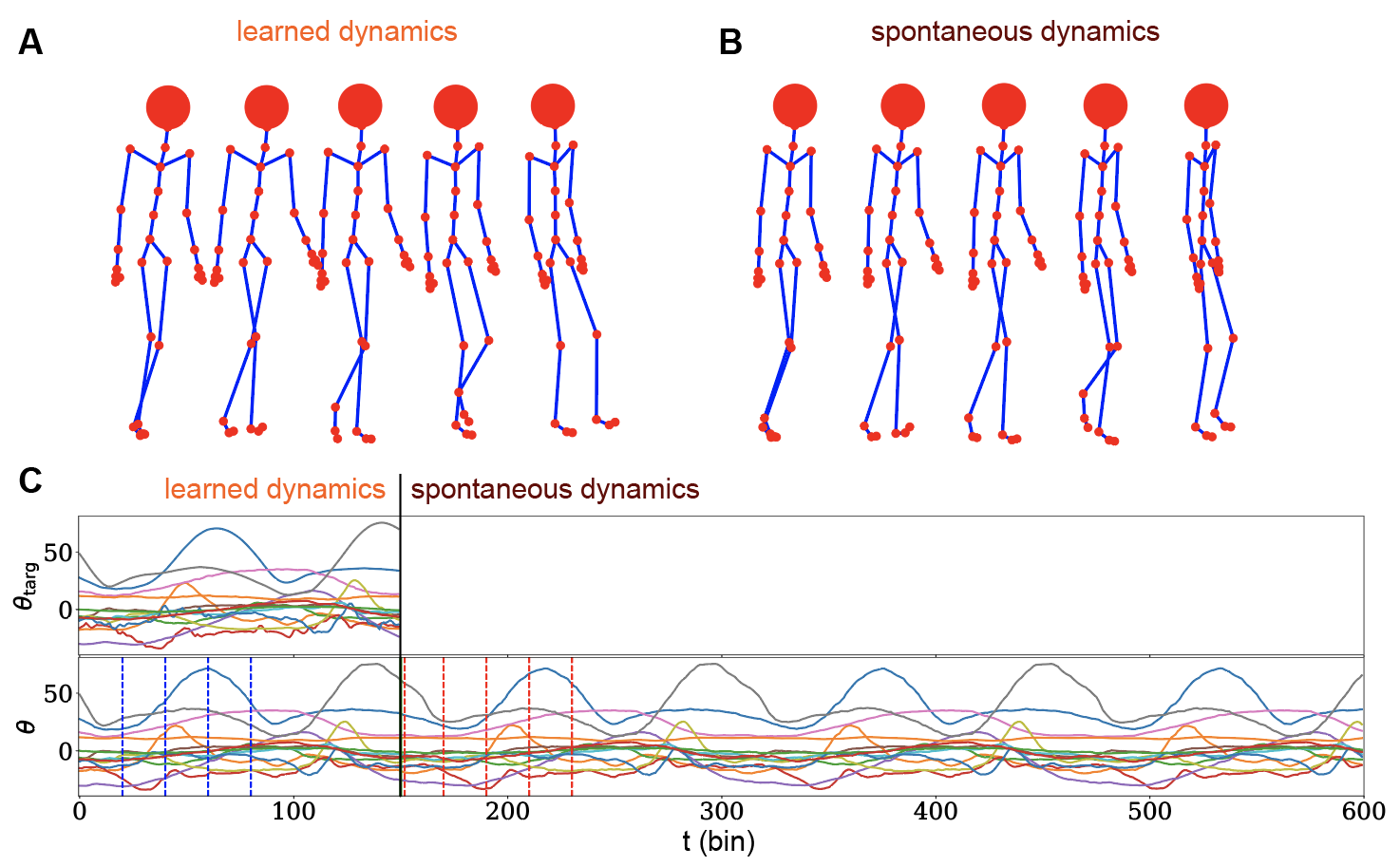
We tested our system on a real-life task: the generation of a 56-dimensional walking dynamics. Our system was trained for 150ms and tested on 600ms, thus providing strong evidence of the generalization capabilities of this model.
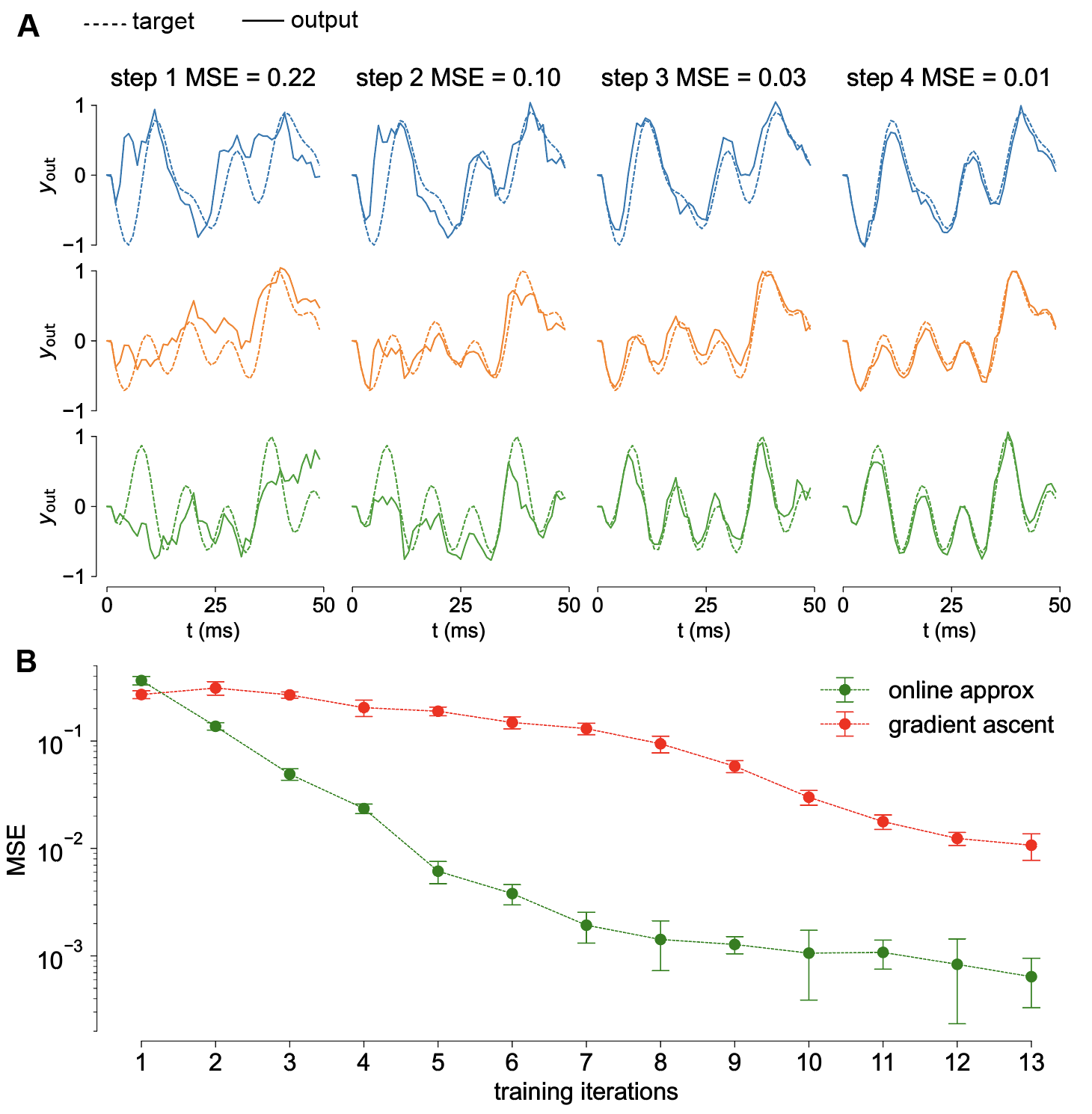
We tested our model on a smaller version of the 3D trajectory task to illustrate how our model achieves very fast convergence to good solutions. We also compare the performance of the online approximation to the exact gradient and found how it is beneficial for performances.
To asses the robustness of our model to noise we corrupt the input current with a zero mean Gaussian noise of increasing variance. Indeed our voltage-dependent training rule proved to be rather stable under input perturbation.