GOAL: The Code Repository

This repository hosts the official implementation of GOAL as described in the paper: Error Based or Target Based? A unifying framework for learning in recurrent spiking networks, Plos Computation Biology (2022).

Overview

The repository is divided into two folders: a primary one src/ and a secondary src/numpy, each one containing the implementation of the same algorithm. The first is built on top of the PyTorch library, which enables native GPU support, while the second is written in pure NumPy (with no GPU support).

Environments

GOAL was tested on Python3 (3.7) and PyTorch (1.6.0). The scripts require the following external libraries to run:

torch
numpy
tqdm
matplotlib # for visualizations

All the packages can be installed via the command pip install <name_of_package>.

Usage

Command Line Interface

We provide a training script train.py for the ND-Trajectory benchmark. To run it, simply navigate to the appropriate folder where train.py is located and launch it via:

python train.py -N 150 -T 150 -O 3 -E 5000 1000 -savepath output.pkl --gpu --verbose

We report the list of supported arguments.

Architecture/Task Parameters

Argument	Required	Default	Description
`-N`, `-n_rec`	✔️	/	Number of recurrent units
`-I`, `-n_inp`	❌	`5`	Number of input units
`-O`, `-n_out`	❌	`3`	Number of output units
`-T`, `-t_seq`	❌	`150`	Lenght of the temporal sequence

Training Parameters

Argument	Required	Default	Description
`-E`, `-epochs`	❌	`(5000, 10000)`	Number of epochs for readout (#1) and recurrent (2) training
`-R`, `-rank`	❌	`None`	Rank of the feedback matrix
`-Rlr`, `-rec_lr`	❌	`5 / sqrt(N)`	Learning rate of recurrent matrix
`-Olr`, `-out_lr`	❌	`0.0025`	Learning rate of readout matrix
`--gpu`	❌	`False`	Flag to signal GPU training
`--resample`	❌	`False`	Flag to trigger resample of feedback matrix at each epoch

Model Parameters

Argument	Required	Default	Description
`-Tm`, `-tau_m`	❌	`8 (dt)`	Membrane time constant
`-Ts`, `-tau_s`	❌	`2 (dt)`	Spike time constant
`-To`, `-tau_o`	❌	`5 (dt)`	Readout time constant
`-Si`, `-sigma_inp`	❌	`22`	Variance of input matrix
`-St`, `-sigma_trg`	❌	`8`	Variance of target matrix
`-Vo`	❌	`-4`	Initial membrane potential
`-B`, `-bias`	❌	`-4`	Unit bias - External field
`-rst`, `-reset`	❌	`-20`	Reset current (after spike)

Misc Parameters

Argument	Required	Default	Description
`-savepath`	❌	`No Saving`	Filepath `.pkl` to store training statistics
`-dt`	❌	`0.001`	Discrete time interval (in seconds)
`--V`, `--verbose`	❌	`False`	Verbose flag

Launching from a Script

Alternatively one can use directly use a script to train a model. Here we provide a minimal example for training on the 3D-Trajectory benchmark.

import torch

from utils import build_target, build_clock
from utils import default, train

par = default

# Setting up computing device
device = 'cuda' if torch.cuda.is_available() and par['gpu'] else 'cpu' 
par['device'] = torch.device(device)

# Building input & target trajectory
par['targ'] = build_target(par['n_out'], T = par['t_seq'],     off = 8).to(par['device'])
par['clck'] = build_clock (par['n_inp'], T = par['t_seq'] - 1, off = 0).to(par['device'])

# Here we train the model
stats = train(par)

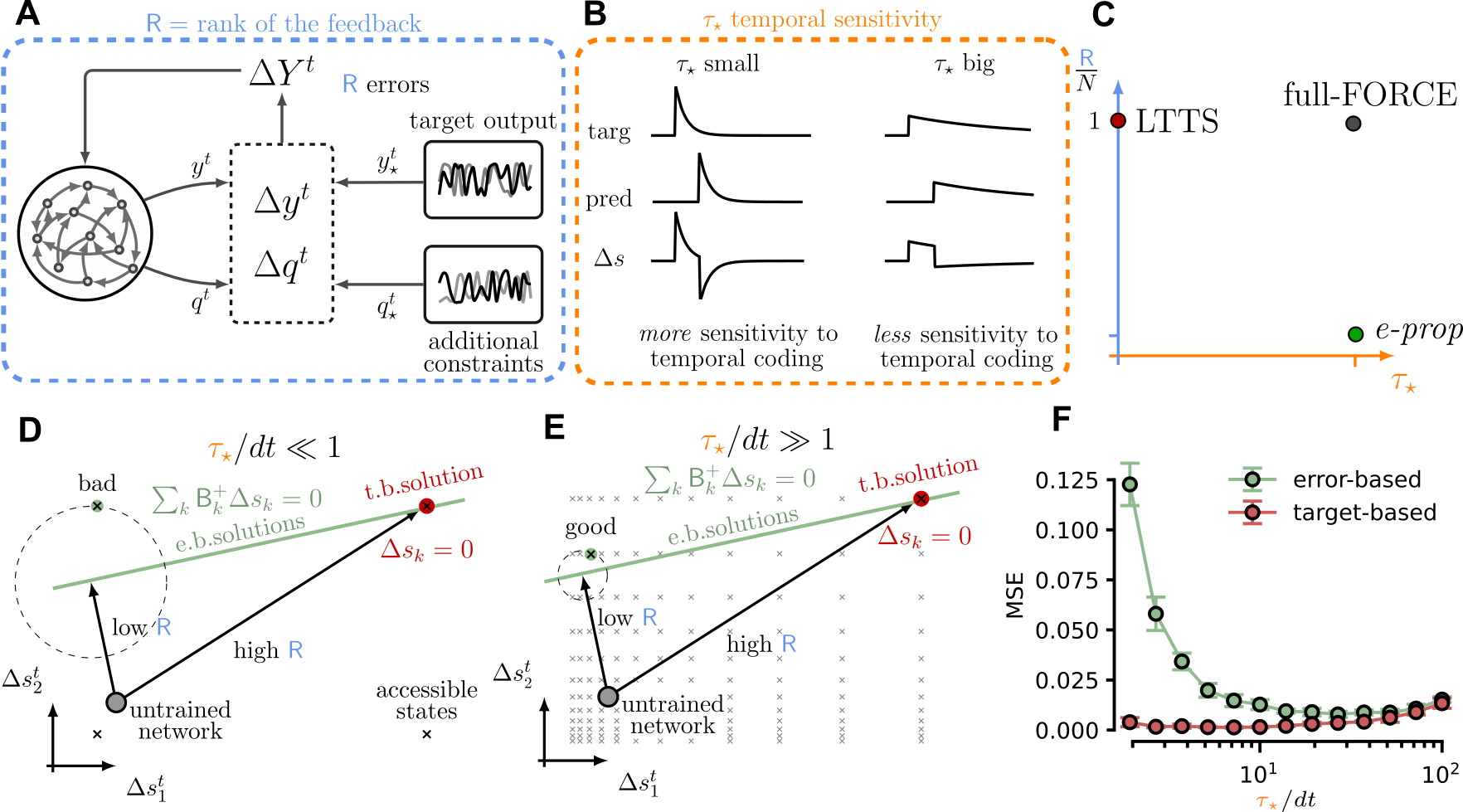
# Optionally save the statistics to file

Results

Our framework generalized apprentiship learning by introducing two key parameters: the feedback matrix rank ${\mathsf{R}}##gh-light-mode-only$ ${\color{white}\mathsf{R}}#gh-dark-mode-only$ and the internal target timescale ${\tau_\star}##gh-light-mode-only$ ${\color{white}\tau_\star}#gh-dark-mode-only$ . By doing so one can describe within a single framework previously distinct algorithms for training recurrent spiking networks and introduce new ones. In the figure below one we represent the core ideas from our work and locate in the ${\left(\mathsf{R},\tau_\star\right)}##gh-light-mode-only$ ${\color{white}\left(\mathsf{R},\tau_\star\right)}#gh-dark-mode-only$ plane previously developped algorithms such as: full-FORCE (target based), e-prop (error-based) and LTTS (target based).

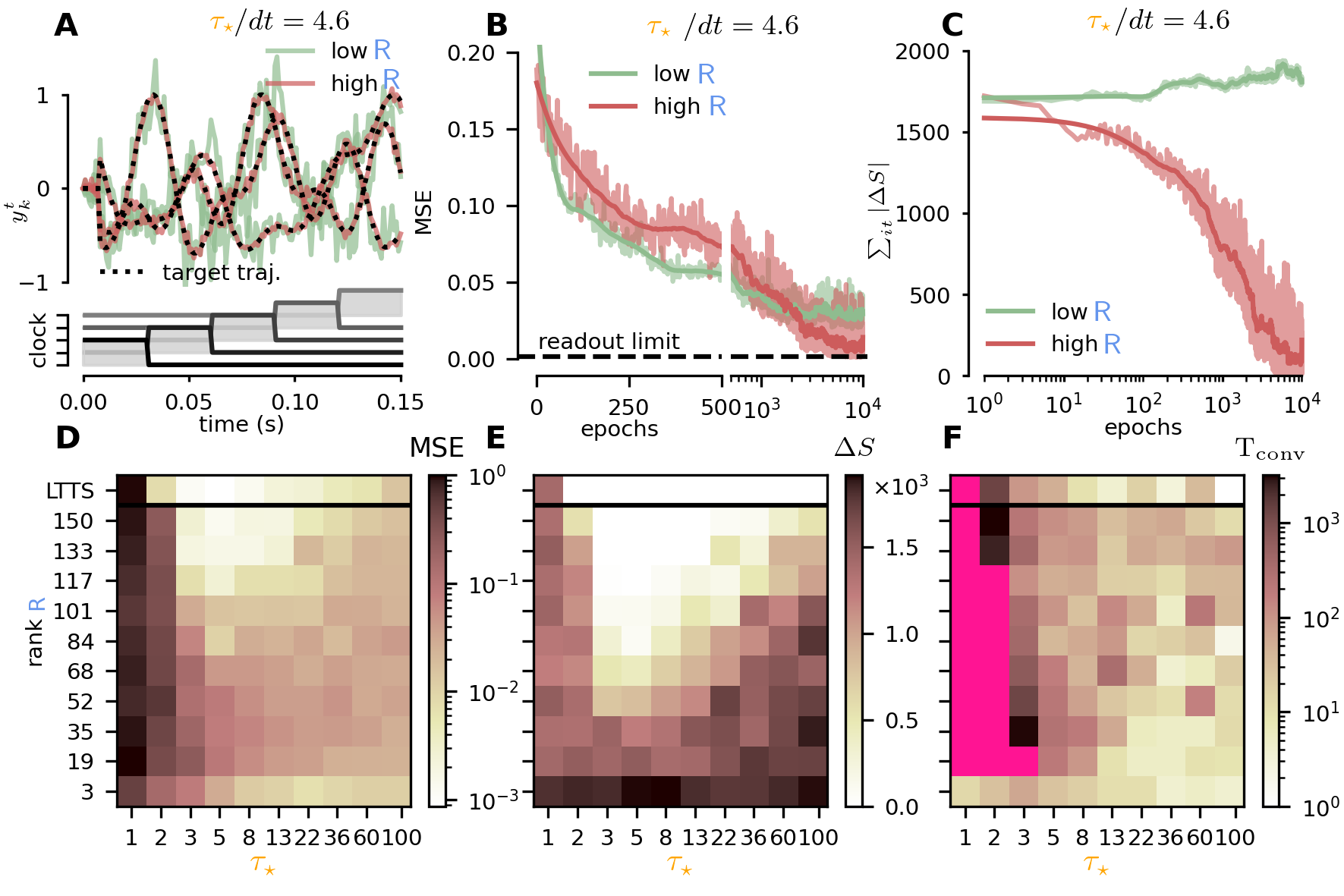
We benchmarked our model on the standard 3D Trajectory task. We studied model training performances (final MSE, final spike-error and convergence speed) for a different values of the two core parameters: the feedback matrix rank ${\mathsf{R}}##gh-light-mode-only$ ${\color{white}\mathsf{R}}#gh-dark-mode-only$ and target timescale ${\tau_\star}##gh-light-mode-only$ ${\color{white}\tau_\star}#gh-dark-mode-only$ . The results of this exploration highlighted two regions of low-output-error corresponding to the two regimes of target- and error-based, with only target-based methods achieving low spike-errors. Interestingly, we found the LTTS algorithm to be quite robust to variation in the ${\tau_\star}##gh-light-mode-only$ ${\color{white}\tau_\star}#gh-dark-mode-only$ parameter.

For a more in-depth discussion (and applications to closed-loop tasks such as Bipedal Walker 2D) refer to our publication.

myscience/goal