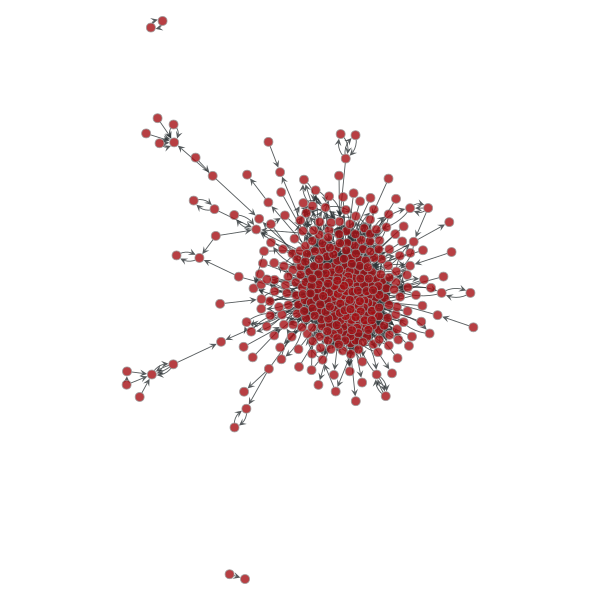
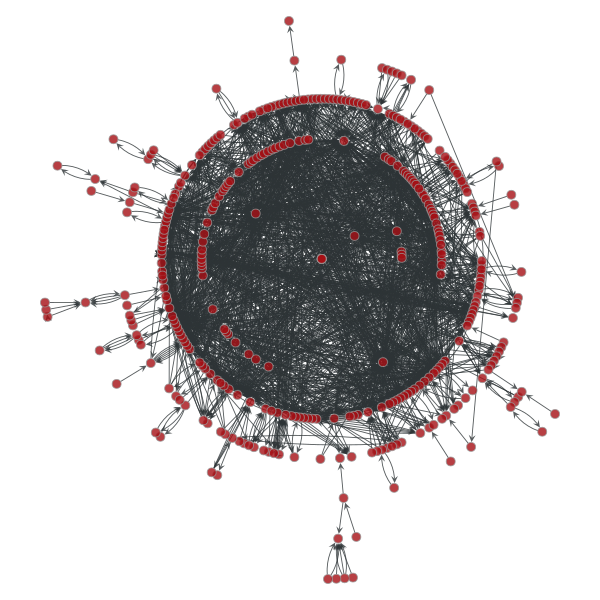
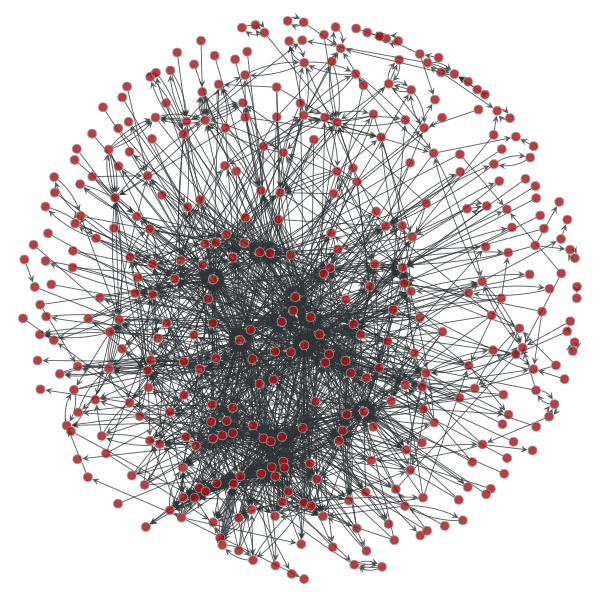
数据为以用户"阿尔卑斯君°"为中心向外bfs搜索得到。
执行src下的gen.sh,在data下生成user.txt,star.txt,relation.txt三个文件。
执行src下的build.py,在data下生成graphAll.xml.gz这个基于graphtools的数据文件。
注意项目中的data文件夹下已经包含了需要下载的数据,数据量还是比较大的,不要轻易git clone .
64452条用户信息,包括: 用户编号,用户编号2(暂时不用),昵称,性别,个性签名 以制表符分割 例:
1000005991 1005051000005991 衷柏夷 他 活在当下,且行且珍惜 福建
1000124571 1005051000124571 工信布 他 互联网科技、经济、生活与宽窄新锐哲思。出版有《互联网时代的浪漫与痛痒——传统行业转型之道》、《嬗变》、《宏声传播集》等。 四川
1000241231 1005051000241231 翡翠羽裳 她 发现近在咫尺的美广东
1000463683 1005051000463683 Ann宝贝琴 她 有一种爱,是信念,从未向时间屈服。 江苏
1000585644 1005051000585644 知心老王 他 心情好,才是真的好! 北京
1000655734 1005051000655734 苏伊finjamie 他 江苏
1000726952 1005051000726952 张毅伟yy 他 上海交通大学EMBA校友会副主席领导力及企业策划专家致力于德鲁克管理的传播 上海
1000830690 1005051000830690 -金浩翔 他 浙江
1000891302 1005051000891302 杨越VJ 他 SMG魅力音乐电视频道总监,VJ,有事电邮yangyue3003@hotmail.com 上海
1001121254 1005051001121254 Rainboy2018 他 北京
6339630条点赞关系,包括: 点赞用户编号,被点赞用户编号,点赞时间 以制表符分割,时间格式为YYYY-MM-DD HH:MM:SS 例:
1000005991 1065618283 2016-07-12 17:16:47
1000005991 1067942913 2015-09-06 21:35:39
1000005991 1101519144 2014-08-30 23:14:13
1000005991 1180514263 2015-06-11 15:05:19
1000005991 1187900115 2014-06-12 19:14:10
1000005991 1189590121 2015-08-28 23:46:37
1000005991 1191965271 2014-08-17 21:54:44
1000005991 1191965271 2016-02-16 11:13:35
1000005991 1195389671 2015-10-05 16:16:09
1000005991 1198367585 2015-09-23 23:43:51
34111736条关注关系,包括: 关注者,被关注者 以制表符分割 例:
1000005991 1004941280
1000005991 1005592945
1000005991 1007262567
1000005991 1007330514
1000005991 1008927295
1000005991 1008965464
1000005991 1009493500
1000005991 1057805991
1000005991 1062133183
1000005991 1067942913
- 使用build.py,对user进行去重,对star和relation中含有溢出用户的条目进行过滤。
- 以user为节点,star和relation为边,构建一个含有重边的连通有向图。
| user vertex | 64422 |
| star edge | 2570280 |
| relation edge | 9051246 |
入度:以某顶点为弧头,终止于该顶点的弧的数目称为该顶点的入度。
出度:以某顶点为弧尾,起始于该顶点的弧的数目称为该顶点的出度。
算法比较简单,复杂度O(|V|),V表示节点个数。
入度的分布与入度的数量大体成反比关系,入度为0的样本不多,有467个,入度为1的样本最多,有7484个,往后则递减,直至入度为37847的有一个。
出度的分布除了出度为0的有1264个之外,其余总体成先上升后下降的过程,在出度为1时,有197个,然后在出度为36时达到极大值311个,接着缓慢下降,直至出度为1947时有1个。
需要注意的是,由于数据源并不是社交网络的全体,而是其中一个连通子图,因此在图的边界会留有很多未来得及遍历的节点,显然他们的出度都为0,因此在出度的分布中才会出现出度为0的特别多的情况。
图的直径:图的直径是指任意两个顶点间距离的最大值.(距离是两个点之间的所有路的长度的最小值)。
算法比较简单,复杂度O(V*V)。
| 直径 | 9 |
| 平均路径长度 | 3.1677261839784396 |
我们统计了数据集中任意两个结点之间最短路的长度,统计之后发现绝大多数的点之间的距离在3以内,分布成先上升后下降的趋势,并且所有的结点之间的距离都不大于9。为了方便演示,我们在图一的基础上对数值取了对数作为图二。
对于节点v的PageRank的值PR(V)被如下定义(根据维基百科):
$$
PR(v) = \frac{1-d}{N} + d \sum_{u \in \Gamma^{-}(v)}
\frac{PR (u)}{d^{+}(u)}
$$
其中
算法复杂度约为O(V+E)。
我们根据pagerank算法对节点进行了统计,并将pagerank的值取了对数,将数据范围划分成了100个区块进行直方图统计。统计之后发现pagerank值在1e-5.65左右的节点最多,在这个数值之前的节点数目最多,这主要是受边界节点的影响。随着pagerank的增加,节点的数目近似反比例下降,直至pagerank最大达到1e-2左右。
由于对数据进行聚类分析等操作复杂度较高,而且大量的数据不利于数据可视化,我们在接下来的分析中采用数据集的一个样本空间进行分析,采样方法如下:
- 在所有节点中,随机采样500个节点,得到点集V';
- 在所有的边中,保留端点均在点集V'中的边,得到边集E;
- 在点集V'中,删除入度和出度均为0的孤立节点,得到新的点集V;
这样我们就得到了一个子图G=(V,E),作为我们接下来使用的样本。
| 最大入度 | 100 |
| 平均入度 | 4.35714285714 |
| 入度方差 | 207.35714285714 |
| 最大出度 | 87 |
| 平均出度 | 6.31034482759 |
| 出度方差 | 206.317479191 |
| 直径 | 11 |
| 平均路径长度 | 3.86344410876 |
| max | 0.036872447021867351 |
| min | 0.00040983606557377055 |
| mean | 0.002243618266165948 |
| variance | 1.3258608835901351e-05 |
Betweenness centrality of a vertex CB(v) is defined as, 顶点v的中介度CB(v)被定义为,
$$ C_B(v)= \sum_{s \neq v \neq t \in V \atop s \neq t}\frac{\sigma_{st}(v)}{\sigma_{st}} $$ where σst is the number of shortest geodesic paths from s to t, and σst(v) is the number of shortest geodesic paths from s to t that pass through a vertex v. This may be normalised by dividing through the number of pairs of vertices not including v, which is (n?1)(n?2)/2.
其中$\sigma_{st}$是从s到t的最短路径的数量,$\sigma_{st}(v)$是从s到t穿过顶点v的最短测路径的数量。这可以通过除以顶点对的数量来进行标准化,也就是除以(n-1)(n-1)/2。
时间复杂度O(VE),空间复杂度O(VE)。
| max | 0.0934646253809 |
| mean | 0.0467323126905 |
| variance | 0.000742529076796 |
| max | 0.0160060035407 |
| mean | 0.00800424936872 |
| variance | 0.0000217695437417 |
对于节点i的样本亲密中心度定义如下: $$ c_i = \frac{1}{\sum_j d_{ij}} $$
其中$d_{ij}$是从i到j的(可能是有向和/或加权的)距离。 如果两个顶点之间没有路径,则此处距离为零。
时间复杂度O(V(V+E))。
| max | 1.0 |
| min | 0.129315389116 |
| mean | 0.319648787918 |
| variance | 0.0346333411029 |
这是一个复杂度为O(V*logV)的绘图算法。 所谓SFDP,是一种多级受力导向(multilevel force-directed placement)的绘图方式。
这个算法是一个复杂度为O(V+E)的绘图算法。 大概**是随机选一个中心点,以这个中心点为根生成一个最小生成树,用节点离中心点的距离代表树中离根节点的距离。
这个算法是一个复杂度为O(V*V)的绘图算法。 所谓ARF,是指"attractive and repulsive forces",即“有吸引力和排斥力”,简而言之,就是将边看成是弹簧,边权越大,弹簧越紧,边的长度越短;边权越小,弹簧越送,边的长度越长,这样就可以生成一个较为清楚的图案。
分块算法主要基于非参数随机块模型(Nonparametric stochastic block model)。 算法复杂度O(VlnVlnV)
我们对随机块模型生成的图中用相同的颜色、相同的图案来表示一个社团。
我们对嵌套随机模型采用了霍尔顿分层(Holden hierarchy)进行可视化,相同颜色的图案表示一个社团,有向箭头表示层级关系。