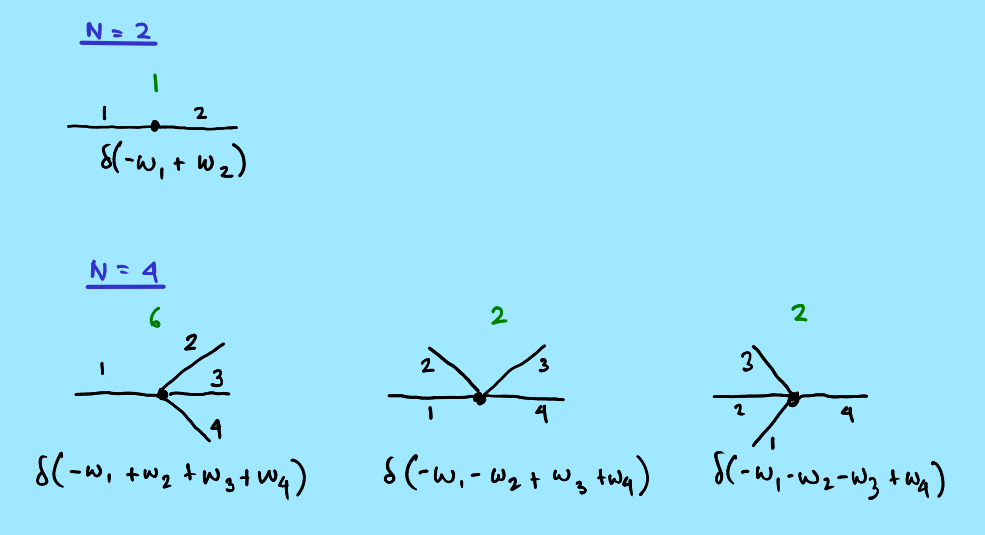A calculator for the phase space of $N$ interacting phonons.
Here I want to calculate how likely different classes of phonon (quantum of lattice vibration) interaction process are. Is $3$-phonon scattering more likely compared to $4$-phonon scattering for a certain phonon? A measure of this likelihood is the scattering phase space. This is essentially a quantification of the amount of the restriction originating from energy and quasimomentum conservation on different classes of phonon interactions. Below I explain further.
First, some notation. I denote a phonon mode by p. A phonon mode is fully described by a wavevector q and a polarization $s$. Phonon 1 is always my sampling phonon. That is, I want to know what the stattering phase space is for phonon 1. Now imagine that we are describing all the $N$-phonon interaction processes. These are the possible interaction paths: phonon 1 can coalesce with $l \in [0, N - 2]$ phonons and decay into $N - l - 1$ phonons. The energy and quasimomentum conservation at the vertex of each interaction is enforced by a $\delta$-function of the form
$$\delta^{x} \equiv \delta \left[ -\omega_{\mathbf{1}} + \sum_{j = 2}^{N} S(x, j - 1) \omega_{\mathbf{j}} \right],$$
where $x \in [1, N - 1]$ is the interaction diagram label, $\omega_{\mathbf{j}}$ is the energy of the phonon mode j, and $S$ is a sign metric defined as $S(x, i) = +$ for $x \leq i$ and $-$ otherwise.
Below I show the interaction diagrams for $2$-phonon (top) and $4$-phonon (bottom) scattering. The lines represent phonons. In general, all lines move from the left to the right. Lines ending at a vertex represents destruction of phonons, whereas lines emitting from the vertex represents creation of phonons. Each diagram has a weight factor, given in green, due to the double counting of indistinguishable phonon states that will happen at a later stage when all but phonon 1 will be integrated over.
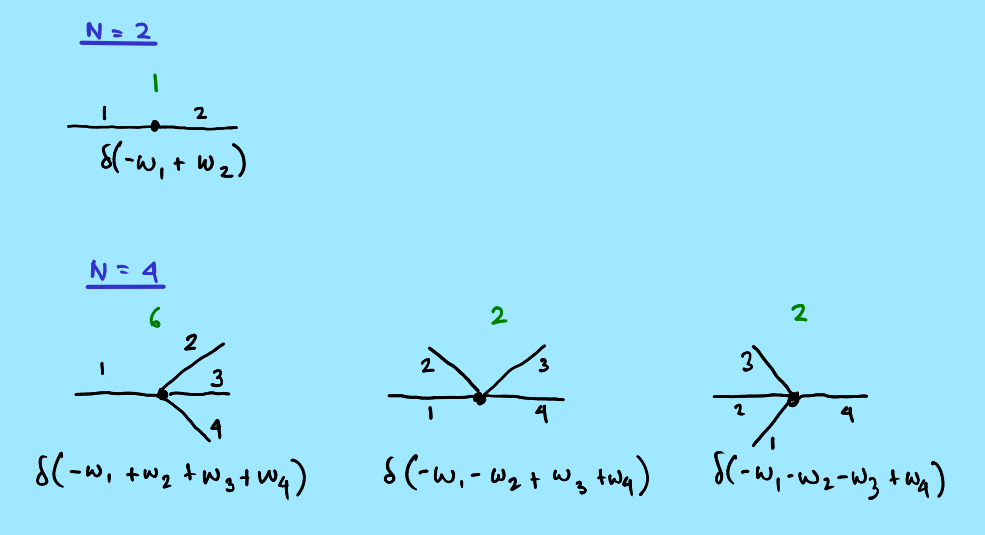
We will need to evaluate integrals of the above diagrams over the non-initial phonons states. For the $N = 2$ case, the result has a special name -- density of states. For the rest, the solution requires adding or subtracting phonon wavevectors and folding them into the first Brillouin zone. We also need to sum over phonon polarizations. Lastly, the expression for the delta function must be constructed on-the-fly and evaulated. For an arbitrary $N$, it will be hard, if not impossible, to do this using imperative programming languages (C/C++, Fortran, python, etc.). The problem seems to be well suited for Common Lisp since the language is  . This is what I am attempting here.
. This is what I am attempting here.
[To be continued...]
. This is what I am attempting here.