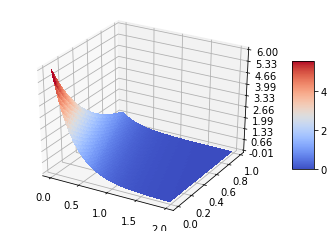
This repository contains my simple and clear to understand implementation of the paper [1]. As an example, I solved the 1D heat partial differential equation.
All the steps are included in a single file: solve_PDE_NN.ipynb which depends on the pytorch and numpy packages.
If you find this implementation useful, then please cite this work:
@software{Doloi_PyTorch_Implementation_of,
author = {Doloi, Nandita},
license = {MIT},
title = {{PyTorch Implementation of Physics Informed Neural Network (PINN)}}
}
This implementation was used in my following paper. Here is the citation:
@article{doloi4477245iterative,
title={Iterative Methods for Neural Networks to Approximate the Solution of Nonlinear Two-Phase Flow Through Porous Media},
author={Doloi, Nandita and Phirani, Jyoti},
journal={Available at SSRN 4477245},
abstract = "{Machine Learning models are often used to make inferences on data that originate from some physical phenomena. For such applications, we might want the inferences to follow the laws of physics. Physics-informed neural networks (PINN) provide us with a mechanism to incorporate physical constraints on the data in the form of differential equations. In this work, we study the use of PINNs in the field of geological reservoirs particularly in solving the Buckley Leverette equation for nonlinear two-phase flow through porous media. PINNs have a tough time solving this equation as it belongs to the class of hyperbolic partial differential equations, which contain discontinuities in the solution. The discontinuity in the solution gives rise to a highly non-convex loss landscape for PINN, and so any second-order quasi-newton optimization method would get stuck in a local minimum and fail to find a good solution unless there is a very good initialization. In this work, we explore two methods which are Graduated optimization and Region based bootstrapping to handle this discontinuity and approximate a better solution to the Buckley Leverette equation as compared to the original PINN optimization. We observed that the loss we were able to achieve were at-least 10 times lower than the baseline.}"
}
paper. Here is the citation:
@proceedings{10.2118/212611-MS,
author = {Doloi, Nandita and Ghosh, Somnath and Phirani, Jyoti},
title = "{Super-Resolution Reconstruction of Reservoir Saturation Map with Physical Constraints Using Generative Adversarial Network}",
volume = {Day 1 Tue, January 24, 2023},
series = {SPE Reservoir Characterisation and Simulation Conference and Exhibition},
pages = {D011S001R006},
year = {2023},
month = {01},
abstract = "{Complete physics-based numerical simulations currently provide the most accurate approach for predicting fluid flow behavior in geological reservoirs. However, the amount of computational resources required to perform these simulations increase exponentially with the increase in resolution to the point that they are infeasible. Therefore, a common practice is to upscale the reservoir model to reduce the resolution such that numerous simulations, as required, can be performed within a reasonable time. The problem we are trying to solve here is that the simulation results from these upscaled models, although they provide a zoomed-out and global view of the reservoir dynamics, however, they lack a detailed zoomed-in view of a local region in the reservoir, which is required to take actionable decisions. This work proposes using super-resolution techniques, recently developed using machine learning methods, to obtain fine-scale flow behavior given flow behavior from a low-resolution simulation of an upscaled-reservoir model. We demonstrate our model on a two-phase, deal-oil, and heterogenous oil reservoir, and we reconstruct the oil saturation map of the reservoir. We also demonstrate how the network can be trained using dynamic coarse geological properties at various resolutions. The findings imply that even when coarse geological features and with limited resolution, the super-resolution reconstructions are able to recreate missing information that is close to the ground facts.}",
doi = {10.2118/212611-MS},
url = {https://doi.org/10.2118/212611-MS},
eprint = {https://onepetro.org/SPERCSC/proceedings-pdf/22RCSC/1-22RCSC/D011S001R006/3060766/spe-212611-ms.pdf},
}
[1] Raissi, Maziar, Paris Perdikaris, and George E. Karniadakis. "Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations." Journal of Computational Physics 378 (2019): 686-707.