This offering is not approved or endorsed by OpenCFD Limited, producer and distributor of the OpenFOAM software via www.openfoam.com, and owner of the OPENFOAM and OpenCFD
and OpenCFD trade marks.
trade marks.
blastFoam is a solver for multi-component compressible flow with application to high-explosive detonation, explosive safety and airblast. The blastFoam solver uses OpenFOAM technology, and is in no way approved or endorsed by OpenCFD Limited, producer and distributor of the OpenFOAM software via www.openfoam.com, and owner of the OPENFOAM and OpenCFD
and OpenCFD trade marks (see Disclaimer above).
trade marks (see Disclaimer above).
blastFoam is free and opensource. blastFoam is currently in pre-release beta, and is being made available primarily to industry, academia, research groups and government. If you'd like to request a copy of the code and solver before the official public release, while we're in beta, just get in touch: info@synthetik-technologies.com
blastFoam is also available on the Texas Advanced Computing Center https://www.tacc.utexas.edu (TACC)
If you use this code for your work or research, please use this citation:
@software{blastfoam:2019,
title = {{blastFoam}: A Solver for Compressible Multi-Fluid Flow with Application to High-Explosive Detonation},
url = {https://github.com/synthetik-technologies/blastfoam},
author = {Synthetik Applied Technologies, {LLC}.},
date = {2019-10-22}
}
blastFoam currently supports the following features:
- An arbitrary number of phases/EOS's
- JWL equation of state with constant, linear, and "Miller" afterburn models
- Multiple example and tutorial cases
- Adaptive mesh refinement (AMR)
- Single and multi-point detonation
- High-order (1st, 2nd, 3rd and 4th order in time; 2nd and 3rd order spatial)
- HLLC, AUSM+, Kurganov, Tadmor flux schemes
- Parallel (MPI)
- Compatible with all of OpenFOAM's standard mesh generation, pre- and post-processing utilities
blastFoam includes the following equations of state:
- Jones Wilkens Lee (JWL) (with afterburn)
- Ideal Gas
- Stiffened Gas
- Cochran-Chan
- Tait
blastFoam has been validated against known solutions to standard gas dynamics problems, and against data from physical tests. Validation cases are included with example/tutorial cases as part of the solver source code.
Reference:
Joachim, Charles E., Gordon W. McMahon, Christo V. Lunderman, and Sharon B. Garner. 1999. “Airblast Effects Research: Small-Scale Experiments and Calculations.” DTIC Document.
Validation against experimental and simulated (CTH) data as reported in Joachim et. al.; see the paper for an explanation of scaling.
Reference:
M. E. Beyer, “Blast Loads Behind Vertical Walls,” Naval Civil Engineering Laboratory, Port Hueneme, CA, USA, AD-A181 274, 1986.
Reference:
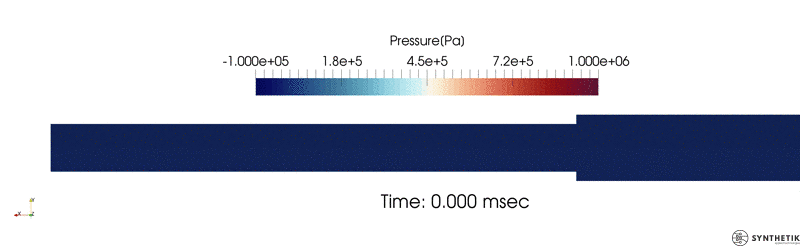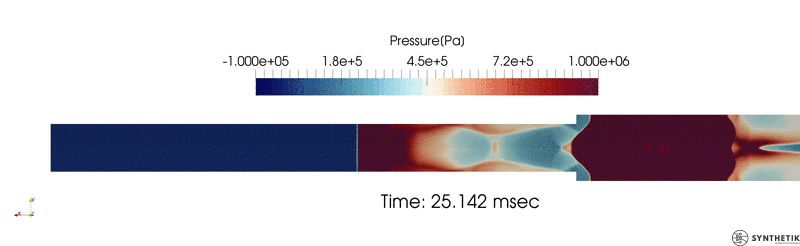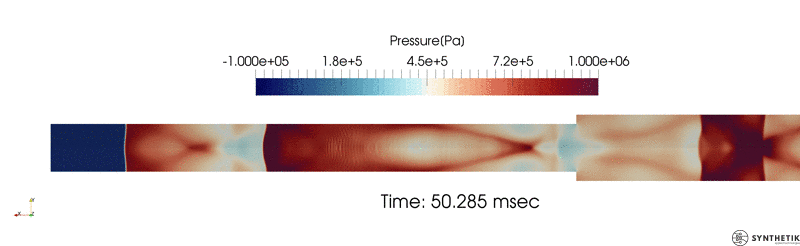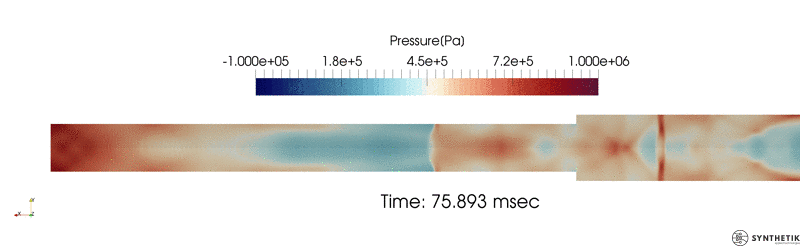
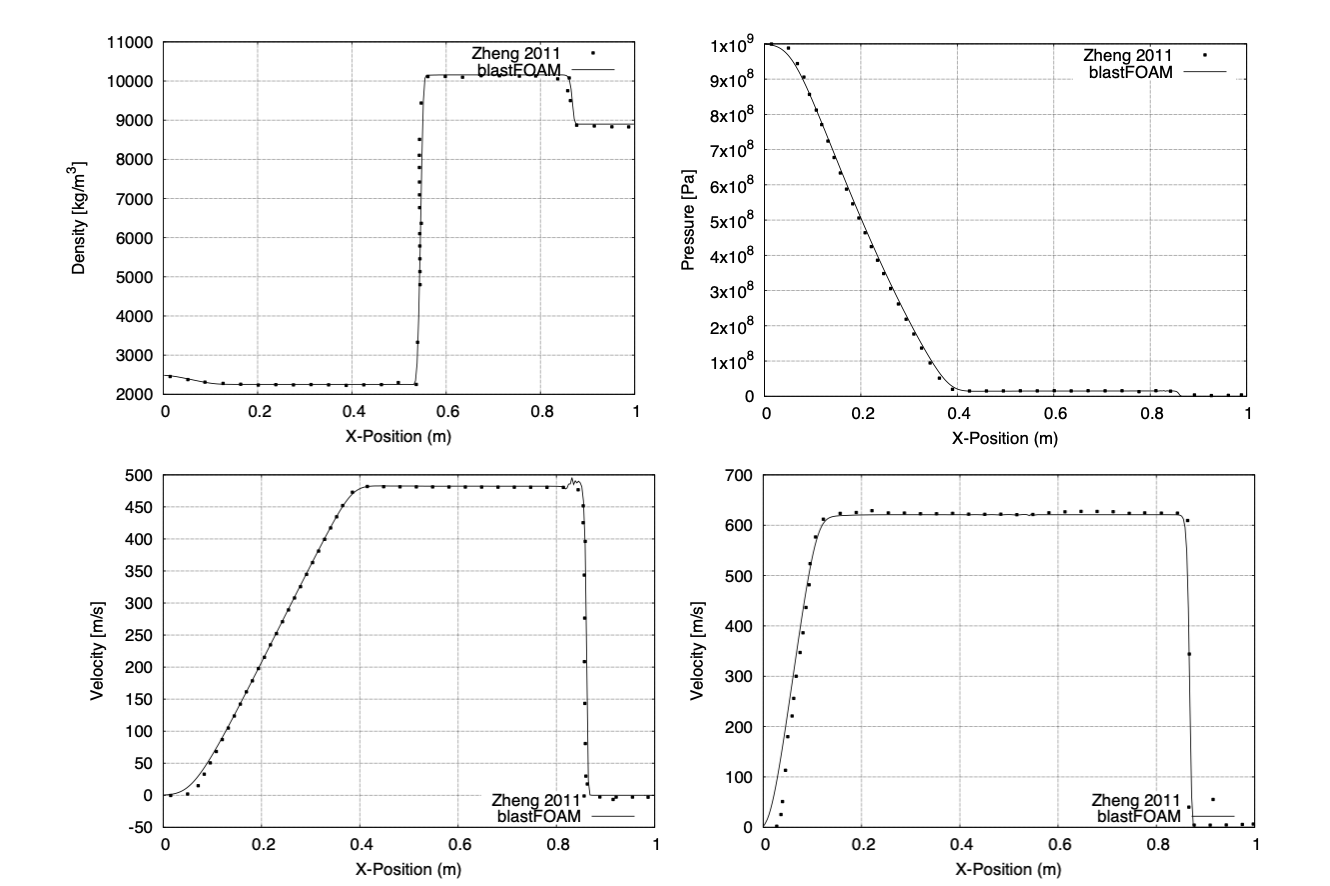
Zheng, H. W., C. Shu, Y. T. Chew, and N. Qin. “A Solution Adaptive Simulation of Compressible Multi-Fluid Flows with General Equation of State.” International Journal for Numerical Methods in Fluids 67, no. 5 (2011): 616–637.
Verification and validation results as compared to those published by Zheng et. al.; HLLC flux shown.
The evolution of a two phase, compressible, and inviscid mixture can be defined by a set of coupled evolution equations for mass, momentum, and energy.
where 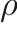 is the mixture density,
is the mixture density, 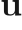 the mixture velocity,
the mixture velocity, 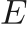 the total energy,
the total energy, 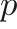 the pressure, and
the pressure, and 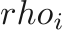 and
and 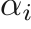 are the density and volume fraction of each phase.
are the density and volume fraction of each phase.
The pressure will be defined using a specified equation of state where the mixture internal energy, densities, and volume fraction are used to calculate the total pressure. The equations of state will be used in the Mie-Gruneisen form.
The mixture pressure is defined using the Mie-Gruneisen from using
where
and 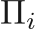 is dependent on the equation of state.
is dependent on the equation of state.
The speed of sound within a give phase is give by
with
and 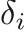 is again dependent on the equation of state.
is again dependent on the equation of state.
For a gas described by the generalized van der Waals equation of state, the pressure is defined as
where 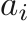 ,
, 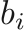 ,
, 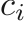 , and
, and 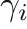 are material parameters. Writing the above equation in M.G. form, we obtain
are material parameters. Writing the above equation in M.G. form, we obtain
and
For a material obeying the Tait EOS, the pressure is defined as
where 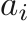 ,
, 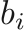 , and
, and 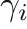 are material properties. In M.G. form, we have
are material properties. In M.G. form, we have
and
For a material obeying the stiffened EOS, the pressure is defined as
where 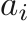 and
and 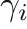 are material properties, and
are material properties, and
The more complicated JWL EOS is often used to define energetic materials, and has a reference pressure given by
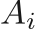 ,
, 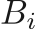 ,
, 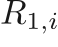 ,
, 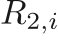 ,
, 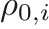 , and
, and 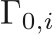 are the material properties. The functions of the EOS are given by
are the material properties. The functions of the EOS are given by
and
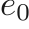 is anther material parameter which denotes a reference energy state.
is anther material parameter which denotes a reference energy state.
The Cochran Chan EOS can be used to describe solid material, and has a reference pressure given by
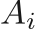 ,
, 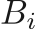 ,
, 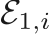 ,
, 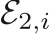 ,
, 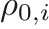 , and
, and 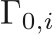 are the material properties. The functions of the EOS are given by
are the material properties. The functions of the EOS are given by
where again, 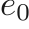 is a material parameter which denotes a reference energy state.
is a material parameter which denotes a reference energy state.


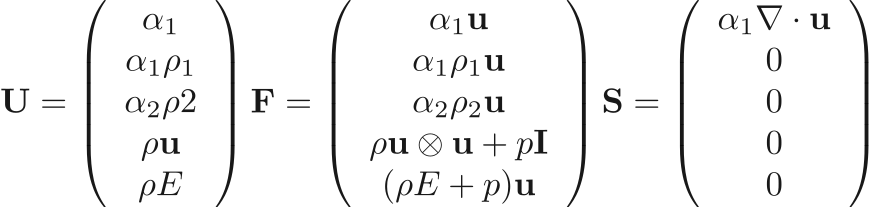
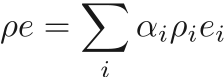
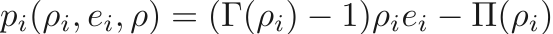
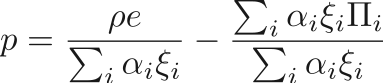
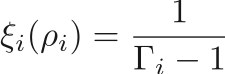
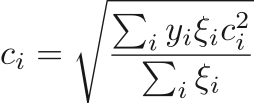
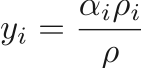
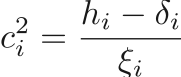
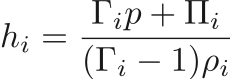
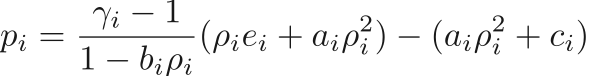
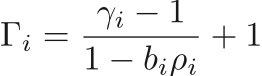
![$$
\Pi_i =
\left[1 - \frac{\gamma_i - 1}{1 - b_i \rho_i}\right] a_i \rho_i^2
+ \left[\frac{\gamma_i - 1}{1 - b_i \rho_i} + 1\right] c_i
$$](https://raw.githubusercontent.com/nene-lee/blastfoam/master/svgs/7ab1654988023cd894bf926eda793c96.png)
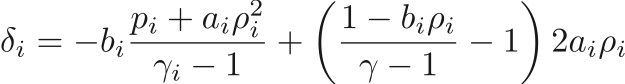
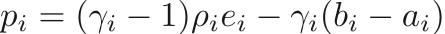
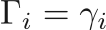
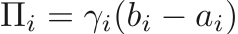
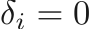
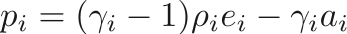
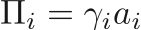
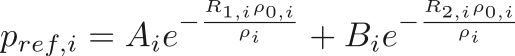
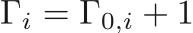
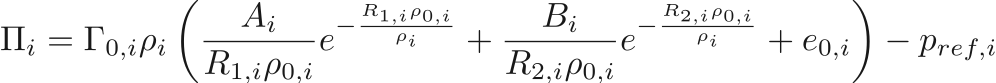
![$$
\delta_i =& \\
&A_i e^{-\frac{R_{1,i} \rho_{0,i}}{\rho_i}}
\left[
\Gamma_{0,i}
\left(
\frac{1}{R_{1,i} \rho_{0,i}}
+ \frac{1}{\rho_i}
\right)
- \frac{R_{1,i} \rho_{0,i}}{\rho_i^2}
\right] \frac{1}{\Gamma_{0,i}} \\
+&B_i e^{-\frac{R_{2,i} \rho_{0,i}}{\rho_i}}
\left[
\Gamma_{0,i}
\left(
\frac{1}{R_{2,i} \rho_{0,i}}
+ \frac{1}{\rho_i}
\right)
- \frac{R_{2,i} \rho_{0,i}}{\rho_i^2}
\right] \frac{1}{\Gamma_{0,i}} \\
+&e_{0,i}
$$](https://raw.githubusercontent.com/nene-lee/blastfoam/master/svgs/abd072e5bd492908795f171d2f8d7a17.png)
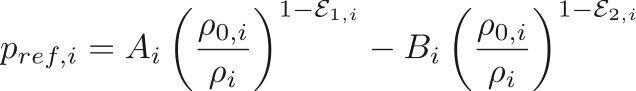
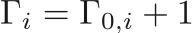
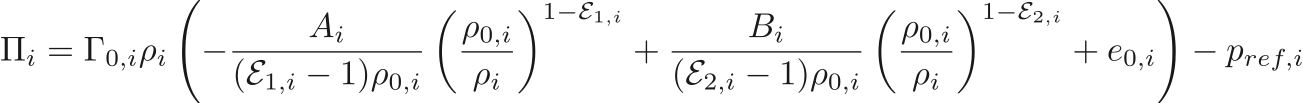
![$$
\delta_i =& \\
&\frac{A_i}{\mathcal{E}_{1,i}}
\left[
\mathcal{E}_{1,i}
\left(\frac{\rho_{0,i}}{\rho_i}\right)^{-\mathcal{E}_{1,i}}
\frac{\mathcal{E}_{1,i} - \Gamma_{0,i} - 1}{\rho_i}
+ \frac{\Gamma_{0,i}}{\rho_{0,i}}
\right] \frac{1}{\Gamma_{0,i}} \\
+&\frac{B_i}{\mathcal{E}_{2,i}}
\left[
\mathcal{E}_{2,i}
\left(\frac{\rho_{0,i}}{\rho_i}\right)^{-\mathcal{E}_{2,i}}
\frac{\mathcal{E}_{2,i} - \Gamma_{0,i} - 1}{\rho_i}
+ \frac{\Gamma_{0,i}}{\rho_{0,i}}
\right] \frac{1}{\Gamma_{0,i}} \\
+&e_{0,i}
$$](https://raw.githubusercontent.com/nene-lee/blastfoam/master/svgs/a2bfd09944f0d0622e5746946fdf45a0.png)