Neslib.MultiPrecision adds two additional floating-point types for use with Delphi. These offer a precision that is up to 4 times larger than that of the Double type.
Neslib.MultiPrecision is build on top of the QD 2.3.22 and works on:
- Windows (32-bit and 64-bit)
- MacOS (64-bit)
- iOS (64-bit, no simulator)
- Android (32-bit and 64-bit)
The algorithms used for these types were developed by David H. Bailey, Yozo Hida and Xiaoye S. Li. Take a look the the QD.pdf file in the C subdirectory if you are interested in the details.
To install:
> git clone https://github.com/neslib/Neslib.MultiPrecisionThis library has no dependencies on other libraries. There are also no run-time dependencies. The underlying C/C++ QD library is linked into the executable using object files or static libraries.
This library defines two additional floating-point types:
DoubleDouble: this is a 128-bit type that has twice the precision of theDoubletype.QuadDouble: this is a 256-bit type that has four times the precision of theDoubletype.
Both types have the same range as the Double type (about ± 10308) but much higher precision. Compared to Single and Double:
| Type | Exponent Bits |
Mantissa Bits |
Precision (decimal digits) |
|---|---|---|---|
| Single | 9 | 24 | 7 |
| Double | 12 | 53 | 16 |
| DoubleDouble | 12 | 106 | 32 |
| QuadDouble | 12 | 212 | 64 |
The names
DoubleDoubleandQuadDoublecome from the underlying QD library. I considered naming theseFloat128andFloat256instead, but there are already official IEEE specifications for such (hardware) types. And since these are not compatible withDoubleDoubleandQuadDouble, I didn't want to add confusion.
The underlying QD library does not use emulation for calculations. Instead, it uses the existing floating-point capabilities of the CPU to use either 2 or 4 Double values to increase the precision. As a result, these types are much faster than other arbitrary/high precision math libraries using the same precision. Also, as opposed to many other libraries, these types don't require dynamic memory allocations, which further helps performance and also reduces memory fragmentation.
The DoubleDouble and QuadDouble types can be used much the same way as the Double type. They support the usual operators (+, -, *, /, =, <>, <, <=, > and >=) as well as most methods available for the record helpers for the Double type (IsNan, IsInfinity, IsNegativeInfinity, IsPositiveInfinity, ToString, Parse and TryParse). There are methods and operators to convert to and from Double, DoubleDouble, QuadDouble and String.
Since the Delphi language doesn't allow you to enter high-precision floating-point literals in source code, the value of a DoubleDouble or QuadDouble variable must be initialized in some other way. There are various options (assuming DD is of type DoubleDouble here):
- Use one of the
Initoverloads. For example,DD.Init(1.23);to initialize aDoubleDoublefrom aDouble. - Use an explicit cast, as in
DD := DoubleDouble(1.23);. - Use one of the predefined constants, as in
DD := DoubleDouble.Pi;. - Or perhaps the easiest way is to just assign a string value, as in
DD := '3.1415926535897932384626433832795';.
I didn't add implicit operators, such as
DD := 1.23;, since those can lead to unintentional conversions that impact performance.
It's important that you call MultiPrecisionInit before performing any DoubleDouble/QuadDouble calculations. This prepares the FPU/CPU for high-precision math. You can use MultiPrecisionReset to restore the FPU/CPU to its previous state.
The default configuration of the library is suitable for most applications. This configuration sacrifices a bit of accuracy for increased speed. If accuracy is more important than speed for your purposes, then you can compile the library with the MP_ACCURATE define. This will make many calculations a bit slower but more accurate.
The underlying QD library (and thus this library) supports a variety of common mathematical functions. In addition, the Neslib.MultiPrecision library adds numerous equivalents of functions found in the System.SysUtils and System.Math units.
| Name | Description |
|---|---|
| StrToDoubleDouble, StrToQuadDouble, StrToDoubleDoubleDef, StrToQuadDoubleDef, TryStrToFloat |
Convert from string |
| FloatToStr, FloatToStrF | Convert to string |
| Inverse | Calculate reciprocal |
| Rem | Calculate remainder, rounding to nearest |
| DivRem | Calculate result of division, including remainder |
| FMod | Calculate remainder, rounded towards zero |
| Sqrt, Sqr | Square root and Square |
| Trunc, Floor, Ceil, Round | Various rounding methods |
| Abs | Absolute value |
| Min, Max | Return minimum or maximum value |
| InRange, EnsureRange | Compare against range |
| SameValue | Approximate equality check |
| Power, IntPower, NRoot, Ldexp, Exp | Exponential functions |
| Ln, LnXP1, Log2, Log10, LogN | Logarithmic functions |
| Sin, Cos, SinCos, Tan | Trigonometric functions |
| ArcSin, ArcCos, ArcTan, ArcTan2 | Inverse trigonometric functions |
| Sinh, Cosh, SinCosh, Tanh | Hyperbolic functions |
| ArcSinh, ArcCosh, ArcTanh | Inverse hyperbolic functions |
| Cotan, Cot, Secant, Sec, Cosecant, Csc | Reciprocal trigonometric functions |
| CotH, SecH, CscH | Reciprocal hyperbolic functions |
| ArcCot, ArcSec, ArcCsc | Reciprocal inverse trigonometric functions |
| ArcCotH, ArcSecH, ArcCscH | Reciprocal inverse hyperbolic functions |
| RadToDeg, RadToGrad, RadToCycle | Convert from radians |
| DegToRad, DegToGrad, DegToCycle | Convert from degrees |
| GradToRad, GradToDeg, GradToCycle | Convert from grads |
| CycleToRad, CycleToDeg, CycleToGrad | Convert from cycles |
A fun way to demonstrate high-precision math is by calculating the Mandelbrot fractal. As you zoom into the fractal, you need more and more precision. The Samples subdirectory contains a FireMonkey application that generates the Mandelbrot fractal at 4 levels of precision (Single, Double, DoubleDouble and QuadDouble).
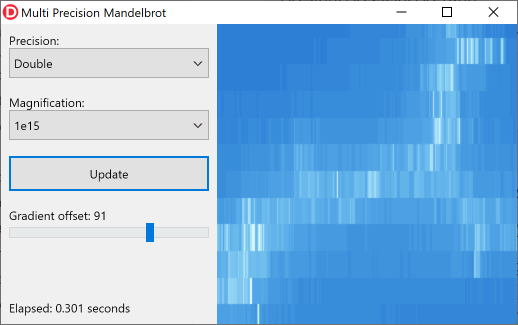
The following image shows a tiny section of the fractal using a magnification of one quadrillion (1015, aka one billiard in Europe) and Double precision:
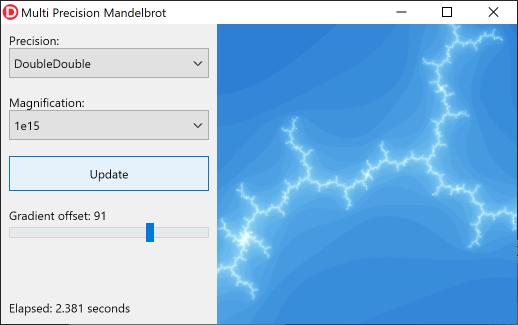
You can clearly see that the Double type doesn't provide enough precision at this magnification level. The DoubleDouble type offers more than enough precision though:
It's not until you reach a magnification level of 1031, that you need to switch to QuadDouble.
There is more to Neslib.MultiPrecision than described above. For more details you can look at the well-documented Neslib.MultiPrecision.pas source file. Additional usage samples can be found in the UnitTests subdirectory and the Mandelbrot sample application.
If you are interested in the technical details and algorithms used for these types, you can take a look at the QD.pdf file in the C subdirectory.
As said, this library is build on top of the QD library. This is a C/C++ library that is linked into your Delphi executable using object files or static libraries. If you ever need or want to build these object files and static libraries yourself, then take a look at the readme.txt file in the C subdirectory for instructions.
Neslib.MultiPrecision is licensed under the Simplified BSD License. See License.txt for details.
The underlying QD library is licensed under the BSD-LBNL License. See the document BSD-LBNL-License.doc in the C subdirectory for details.