The Electrical Engineering Calculations for Python module is a collection of classes for simple to complex electrical calculations, with a special focus on handling tolerances.
USE AT OWN RISK, I DO NOT GUARANTEE THE CORRECTNESS OF THE CALCULATIONS IN THIS PACKAGE
The eecalpy package is available on the Python Package Index (PyPI). The package needs Python 3+, you can install it with:
$ pip install eecalpy
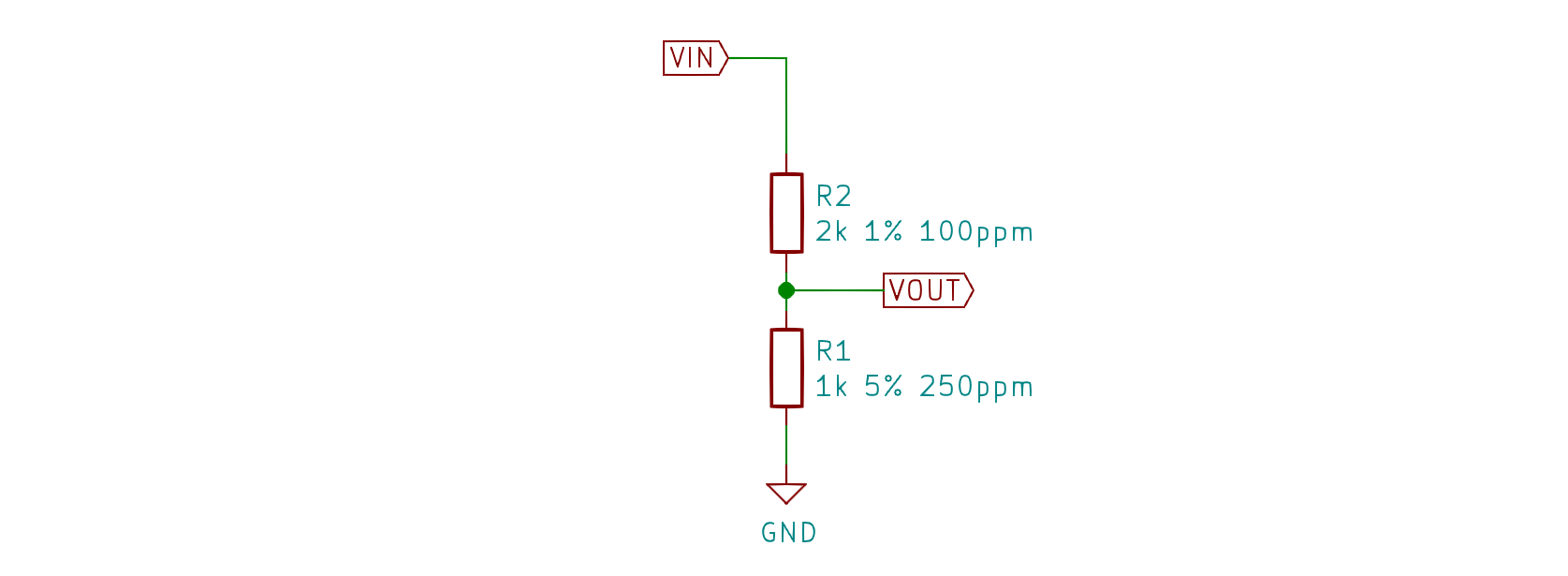
Check out the voltage divider below. For both resistors their tolerance and the temperature coefficient α are given (α in parts per million).
Let's create two variables for them.
>>> r1 = R(resistance=1000, tolerance=0.05, alpha_ppm=250)
>>> r2 = R(2e3, 0.01, 100)
>>> r1; r2
1.0kΩ ± 5.0% (± 50.0Ω) [0.9500 .. 1.0500]kΩ @ 20°C α=250ppm
2.0kΩ ± 1.0% (± 20.0Ω) [1.9800 .. 2.0200]kΩ @ 20°C α=100ppm
The formula for the voltage divider factor is r1 / (r1 + r2). To calculate it use R.voltage_divider(other_resistor):
>>> r1.voltage_divider(r2)
0.33 ± 4.0% [0.3199 .. 0.3465]
You can also use a shorthand notation:
>>> r1 // r2
0.33 ± 4.0% [0.3199 .. 0.3465]
Attention: Do not use the statement r1 / (r1 + r2) here, because it would use the tolerance limits
of r1 twice (addition and division) and therefore yield a false result.
The result above is an instance of the Factor class. Now only the voltage is missing.
These are created using U(voltage, tolerance=0.0).
Let's assume the input voltage is 24V with a 1% tolerance the output voltage of the voltage divider then is:
>>> vin = U(24, 0.01)
>>> vout = r1 // r2 * vin
>>> vout
8.0V ± 5.0% (± 400.0mV) [7.6000 .. 8.4000]V
Note: the statement vout = vin * r1 // r2 does not work. It's evaluated from left to right, so python first tries vin * r1 which is not implemented (voltage times resistance), but you can always use parenthesis:
>>> vin * (r1 // r2)
8.0V ± 5.0% (± 400.0mV) [7.6000 .. 8.4000]V
For demonstration, let's calculate some of the voltage divider parameters.
Current through R1 and R2 (to GND):
>>> vin / (r1 + r2)
8.01mA ± 3.33% (± 266.81µA) [7.7394 .. 8.2730]mA
Power dissipation of the resistors:
>>> vout**2 / r1
65.46mW ± 21.35% (± 13.97mW) [51.4842 .. 79.4301]mW
>>> (vin - vout)**2 / r2
128.26mW ± 12.3% (± 15.78mW) [112.4776 .. 144.0351]mW
Let's also see how vout changes when the ambient temperature is 200°C:
>>> r1.at_T(200) // r2.at_T(200) * vin
8.14V ± 4.97% (± 404.16mV) [7.7359 .. 8.5443]V
R.at_T(temperature) is the same as R.at_temperature(temperature).
It returns a new resistor object at the given temperature (in °C).
You can of course also use perfect values, so without the tolerance and temperature coefficient:
>>> r1 = R(1e3)
>>> r2 = R(2e3)
>>> vin = U(24)
>>> r1; r2; vin
1.0kΩ @ 20°C
2.0kΩ @ 20°C
24.0V
>>> vout = r1 / (r1 + r2) * vin
>>> vout
8.0V
By the way, you can get the series resistance using + and the parallel
resistance using |:
>>> r1 + r2
3.0kΩ @ 20°C
>>> r1 | r2
666.67Ω @ 20°C
>>> r1 | (R(5e3) + R(3e3)) | r2 # complex statements allowed!
615.38Ω @ 20°C
The available classes are:
- Voltage
U(voltage, tolerance=0.0) - Resistance
R(resistance, tolerance=0.0, alpha_ppm=None) - Current
I(current, tolerance=0.0) - Power
P(power, tolerance=0.0) - Energy
E(energy, tolerance=0.0) - Time
Time(time, tolerance=0.0 - Factor
Factor(factor, tolerance)(unitless factor, example below) - squared Voltage (V²)
Usq(voltage, tolerance=0.0) - squared Current (A²)
Isq(voltage, tolerance=0.0)
All classes do have the following members (example when using a voltage):
>>> v1 = U(24, 0.04)
>>> v1
24.0V ± 4.0% (± 960.0mV) [23.0400 .. 24.9600]V
>>> v1.value
24
>>> v1.min
23.04
>>> v1.max
24.96
>>> v1.unit
'V'
A unit can also be created using the .from_min_max(min, max) classmethod when
the lower and upper limit is known (min/max):
>>> P.from_min_max(3, 4)
3.5W ± 14.29% (± 500.0mW) [3.0000 .. 4.0000]W
All units feature the add, subtract, multiply and divide operators. The calculation only works if the result's type is one of the classes above:
This works because the result type is one of the known classes:
>>> U(10) + U(20)
30.0V
>>> I(2e-3) - I(10e-3)
-8.0mA
>>> U(10) * I(2e-3)
20.0mW
>>> U(10) / I(2e-3)
5.0kΩ @ 20°C
>>> U(10) * Factor(2)
20.0V
>>> I(10e-3) * R(150)
1.5V
>>> P(200) / U(5)
40.0A
>>> U(3) * U(3)
9.0V²
>>> U(3)**2 # U squared
9.0V²
>>> U(3)**2 / R(1e3)
9.0mW
This does not work because voltage divided by power is not a known class:
>>> U / P
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for /: 'type' and 'type'
One of the approaches is to use eecalpy inside a script as shown above. Here's my recommendation:
import eecalpy as ee
r1 = ee.R(1e3)
u1 = ee.U(5)
...
There is a parser that comes with eecalpy. It is not completely finished yet and some expressions do not yet work. It can be used for simple expressions though, like:
from eecalpy.parser import parse_expression as pe
r1 = pe('150k 1%') # 150kΩ 1% resistor
u1 = pe('5V')
i1 = pe('100mA')
t1 = pe('200µs')
u1 * i1 * t1
>>> 100.0µJ
When installing eecalpy, the eecalpy console command is also installed and can be called from the command line. This opens a REPL where eecalpy scripts can be executed:
PS C:\Users\wese3112> eecalpy console
» u1 = 5V 1%
u1 = 5.0V ± 1.0% (± 50.0mV) [4.9500 .. 5.0500]V
» i1 = 10mA
i1 = 10.0mA
» t1 = 200µs
t1 = 200.0µs
» u1 * i1 * t1
10.0µJ ± 1.0% (± 100.0nJ) [9.9000 .. 10.1000]µJ
»