The KL-divergence is normally defined between two probability distributions. In the case where only samples of the probability distribution are available, the KL-divergence can be estimated in a number of ways.
Here I test a few implementations of a KL-divergence estimator based on k-Nearest-Neighbours probability density estimation.
The estimator is that of
Qing Wang, Sanjeev R. Kulkarni, and Sergio Verdú. "Divergence estimation for multidimensional densities via k-nearest-neighbor distances." Information Theory, IEEE Transactions on 55.5 (2009): 2392-2405.
Samples are drawn from various test distributions, and the estimated KL-divergence between them is computed. Uncertainties are assessed by re-sampling the distributions and re-computing divergence estimates 100 times. Uncertainty bands are then given as the interval containing 68% of the re-sampled estimates closest to the median. Timings where provided are the time taken for the computation of all 100 re-samples on a sample size of N=1000 with k=5.
This study is far from exhaustive, and timings are sensitive to implementation details. Please take with a pinch of salt.
-
naive_estimator
KL-Divergence estimator using brute-force (numpy) k-NN
-
scipy_estimator
KL-Divergence estimator using scipy's KDTree
-
skl_estimator
KL-Divergence estimator using scikit-learn's NearestNeighbours
-
skl_efficient
An efficient version of the scikit-learn estimator by @LoryPack
These estimators have been benchmarked against slaypni/universal-divergence.
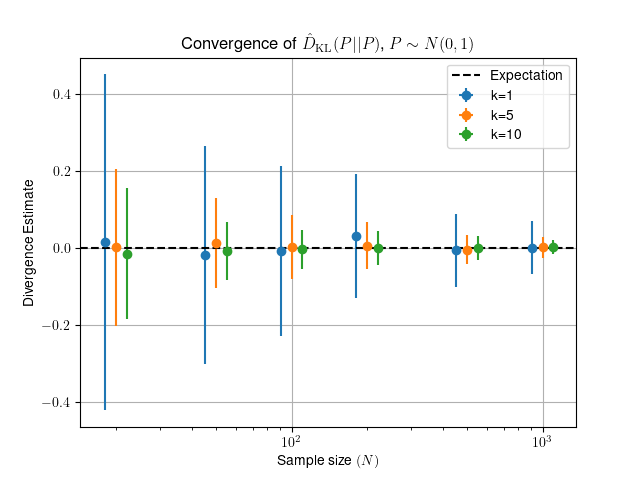
Estimate the divergence between two samples of size N and dimension 1, drawn from the same ~ N(0,1) probability distribution. The expected value for the divergence in this test is D=0.
| Estimator | D(P|Q) | Time (s) |
|---|---|---|
| naive_estimator | 1.595e-03 | 7.998 |
| scipy_estimator | 1.595e-03 | 0.111 |
| skl_estimator | 1.595e-03 | 18.427 |
| skl_efficient | 1.595e-03 | 0.147 |
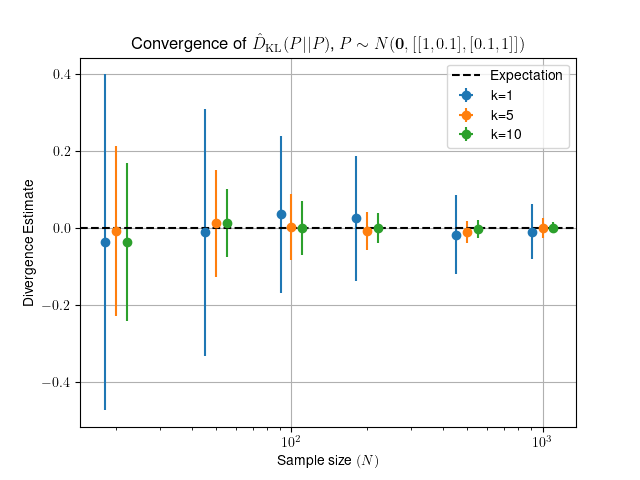
Estimate the divergence between two samples of size N drawn
from the same 2D distribution with
mean=[0,0] and covariance=[[1, 0.1], [0.1, 1]].
The expected value for the divergence in this test is D=0.
| Estimator | D(P|Q) | Time (s) |
|---|---|---|
| naive_estimator | -6.811e-04 | 9.931 |
| scipy_estimator | -6.811e-04 | 0.182 |
| skl_estimator | -6.811e-04 | 18.362 |
| skl_efficient | -6.811e-04 | 0.222 |
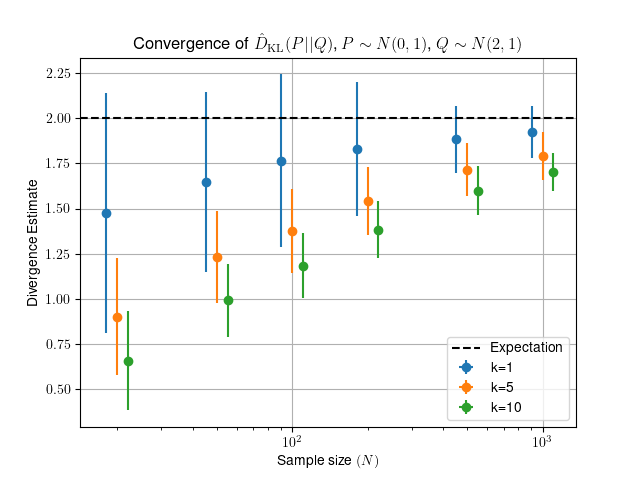
Estimate the divergence between two samples of size N and dimension
1. The first drawn from N(0,1), the second from N(2,1).
The expected value for the divergence in this test is D=2.0.
| Estimator | D(P|Q) | Time (s) |
|---|---|---|
| naive_estimator | 1.790e+00 | 7.014 |
| scipy_estimator | 1.790e+00 | 0.105 |
| skl_estimator | 1.790e+00 | 18.215 |
| skl_efficient | 1.790e+00 | 0.139 |
Start in a clean python 3.10 environment and run the following
# Setup dependencies
pip install -r requirements.txt
# Run the tests and generate the figures
./src/run_tests.py
# Add the header and footer to the report
cat templates/header.md report.md templates/footer.md > README.mdWhich will then likely take some time to complete.
The number of resamples used to estimate uncertainties is defined by
n_resamples in tests.py. This is naturally an extremely sensitive variable
for how long the tests take to run.