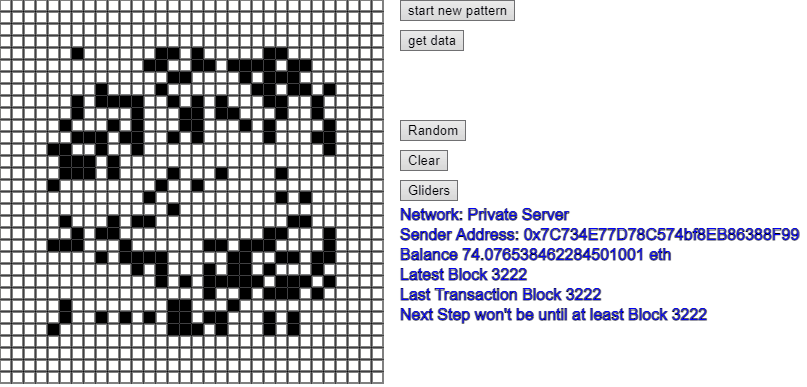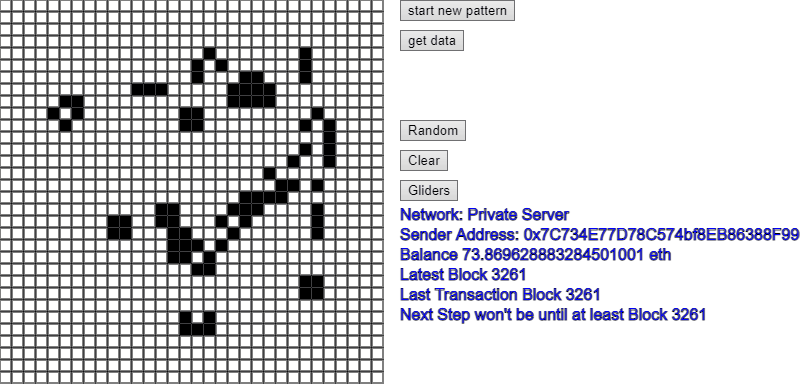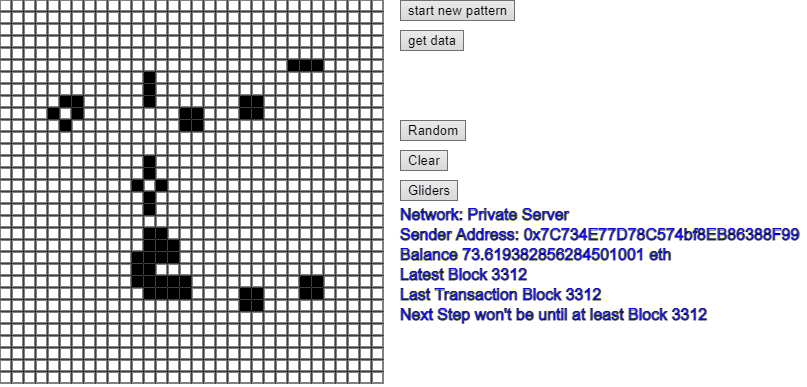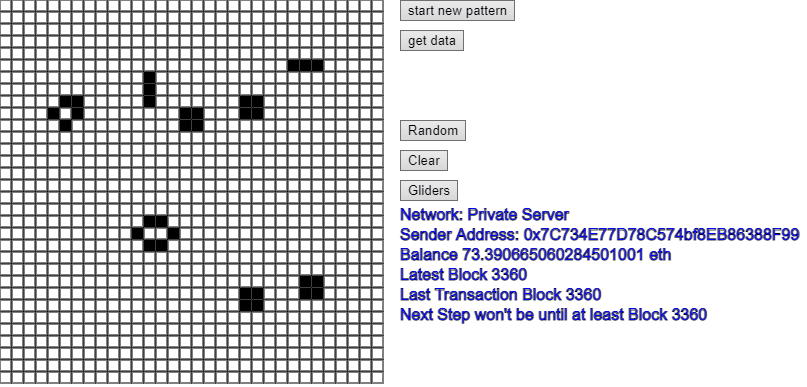
The world's most expensive implementation of Conway's Game of Life ever - over $2,000 per step! (Probably the slowest too!)
Conway's Game of Life running as a smart contract on the Ethereum Blockchain.
This application would be able to run 'forever' - so long as there was some funds in an Ethereum account that could be used to run each 'step'.
However, the cost of Ethereum (and therefore 'gas') used to run smart contracts is so high that it would cost (in March 2021) over $80 just to register the smart contract, and to run a single 'step' of the game would cost over $2,000! No doubt that the code could be made more efficient and consume less resources, but hey that's just too much work for a concept app, so I have simply registered the contract on the Kovan test network instead, and use some 'fake' Ethereum to run the system. The app is the same, but it just points to the 'Kovan' test network instead of the Ethereum mainnet.
You can see it in action here
The application consists of three parts:
- Front end Javascript application using the p5js library which runs in your browser
- A Python Flask app implemented as a google cloud function
- An Ethereum smart contract written in Solidity which runs on the (Kovan) Ethereum blockchain
There are just three files in the app: a very simple index.html to host the javascript application in sketch.js along with a simple style.css stylesheet. When started, the app requests the 32x32 grid from the blockchain (via the flask app). Every minute or so the app will trigger a 'step' in the smart contract. There are a couple of other buttons that will create a random selection on the screen, clear the screen, and add a few gliders. You can also use the mouse to select/deselect individual cells. Press the start new pattern button to send your pattern to the smart contract.
This started as a bog standard Flask application, but I converted it into a google cloud function to avoid the hassle of having to host it somewhere.
Most of the functionality here could have also been included in the browser-based javascript application, but because of my greater familiarity with python and my uncertainty about how to secure the private key needed to sign the solidity transactions I left it running on the server side.
The main.py needs some environment variables for it to work. These are configured as part of the deployment script when pushing the flask app to the google cloud service:
gcloud functions deploy gameoflife \
--runtime python38 \
--trigger-http \
--allow-unauthenticated \
--env-vars-file env.yaml
env.yaml:
---
network_name: Kovan
HTTPProvider: 'https://kovan.infura.io/v3/PUT-YOUR-INFURA-KEY-HERE'
contract_address: '0x51B92cef4C0847EF552e4129a28d817c26a4A053'
private_key: 'PUT-THE-PRIVATE-KEY-OF-YOUR-ACCOUNT-HERE'
chain_id: '42'
The smart contract was written in Solidity. I used VS Code with a solidity extension that highlighted any syntax errors. The testing of the contract was done with the Truffle/Ganache suite of applications, and to get it onto the blockchain I simply used the remix online tool with the metamask browser extension.
I decided that a 32 x 32 cell structure would be big enough the showcase how the game works. In order to reduce the size requirements of data to be stored on the block chain, I used an array of 4 x 256 bit unsigned integers and used this as a bit field. There are three entry points in the contract (apart from the constructor): setCells(), getCells() and step()
The step function mainly consists of loop iterating through the cells, creating/removing cells according to the rules of the game. I didn't make much effort to reduce the amount of work done in order to run a single cell, so I did run foul of one specific issue - the amount of gas consumed. At times it would exceed the limits of even the test networks, and so I ignored some of the cells on the edge of the whole cell universe. It would then take about 11M gas to process it, which is just below the 12M limit for the Kovan network.
for (int16 row=4; row<rows-4; row++) {
for (int16 col=4; col<cols-4; col++) {
int16 pos = (col + row*cols);
int count = 0;
// count_neighbours - count the number of cells that are direct neighbours
count += get(pos - cols - 1); //(row-1,col-1);
count += get(pos - cols); //(row-1,col );
count += get(pos - cols + 1); //row-1,col+1);
count += get(pos - 1); //(row,col-1);
count += get(pos + 1); //(row,col+1);
count += get(pos + cols -1); //(row+1,col-1);
count += get(pos + cols); //(row+1,col );
count += get(pos + cols + 1); //(row+1,col+1);
// if current cell is alive
if (get(pos) == 1) {
if (count > 3) {
set(pos,0);
} else if (count == 2 || count == 3) {
set(pos,1);
} else if (count < 2) {
set(pos,0);
}
} else { // dead cell
if (count == 3) {
set(pos,1);
}
}
}
}
and the get and set functions are implemented as bit twiddlers.
function set(int16 pos, int8 value) internal {
// the linear array is held in 4 x 256 unsigned integers
uint32 i = uint32(pos) / 256;
uint32 j = uint32(pos) % 256;
// if value is 1 then set the j-th bit
if (value>0){
newcells[i] |= (1 << j); // set this bit
} else {
newcells[i] &= ~(1 << j); // turn off this bit
}
}
function get(int32 pos) view internal returns (int) {
if (pos<0) {
pos += rows*cols;
}
if (pos >= rows*cols) {
pos -= rows*cols;
}
// make sure pos always is a valid value
pos = pos % int32(rows*cols);
// the linear array is held in 4 x 256 unsigned integers
uint32 i = uint32(pos) / 256;
uint32 j = uint32(pos) % 256;
// if the j-th bit set?
if ((cells[i] >> j) & 0x01 == 1 ) {
return 1;
} else {
return 0;
}
}