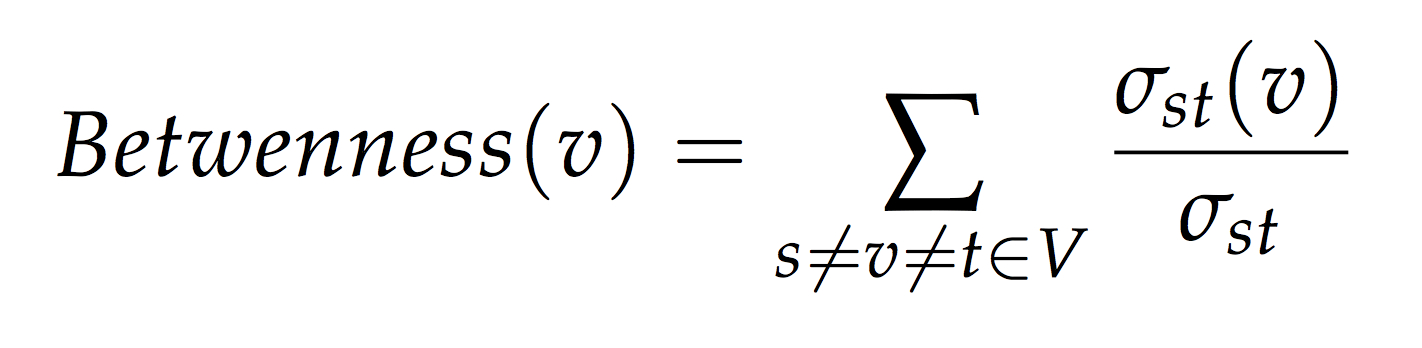Introduction:
Emergency physicians, like other specialists, are faced with different patients and various situations every day. They have to use ancillary diagnostic tools like laboratory tests and imaging studies to be able to manage them (1-8). In most cases, numerous tests are available. Tests with the least error and the most accuracy are more desirable. The power of a test to separate patients from healthy people determines its accuracy and diagnostic value (9). Therefore, a test with 100% accuracy should be the first choice. This does not happen in reality as the accuracy of a test varies for different diseases and in different situations. For example, the value for diagnosing cancer varies based on pre-test probability. It shows high accuracy in low risk patient and low accuracy in high risk ones. The characteristics of a test that reflects the aforementioned abilities are accuracy, sensitivity, specificity, positive and negative predictive values.
Definitions:
-
Patient: positive for disease
-
Healthy: negative for disease
-
True positive (TP) = the number of cases correctly identified as patient
-
False positive (FP) = the number of cases incorrectly identified as patient
-
True negative (TN) = the number of cases correctly identified as healthy
-
False negative (FN) = the number of cases incorrectly identified as healthy
Accuracy: The accuracy of a test is its ability to differentiate the patient and healthy cases correctly. To estimate the accuracy of a test, we should calculate the proportion of true positive and true negative in all evaluated cases. Mathematically, this can be stated as:
Accuracy = TP + TN /TP + TN + FP + FN
Sensitivity (Recall): The sensitivity of a test is its ability to determine the patient cases correctly. To estimate it, we should calculate the proportion of true positive in patient cases. Mathematically, this can be stated as:
Sensitivity = TP / TP + FN
Precision: The Precision of a test is its ability to determine how many of the patients cases were relevant.
Precision = TP / TP + FP
Specificity: The specificity of a test is its ability to determine the healthy cases correctly. To estimate it, we should calculate the proportion of true negative in healthy cases. Mathematically, this can be stated as:
Specificity = TN / TN + FP
Examples: For each of the following calculate the Accuracy, Sensitivity, Precision and Specificity.
-
Imagine we have a sample of 100 cases, 50 healthy and the others patient. If a test can be positive for all patients and be negative for all the healthy ones. it is 100% accurate.
-
If the test can only diagnose 25 out of the 50 patients and has reported the others as healthy.
-
This time we will assume that the test has been able to identify 25 of the 50 healthy cases and has reported the others as patients.
Introduction
Many medical applications, we have datasets where we have two classes for the main outcome; normal samples and relevant samples. For example in a cancer detection application we might have a small percentages of patients with cancer (relevant samples) while the majority of samples might be healthy individuals.
The main motivation behind the need to preprocess imbalanced data before we feed them into a classifier is that typically classifiers are more sensitive to detecting the majority class and less sensitive to the minority class. Thus, if we don't take care of the issue, the classification output will be biased, in many cases resulting in always predicting the majority class.
Definitions
-
Undersampling: This method works with majority class. It reduces the number of observations from majority class to make the data set balanced. Random undersampling method randomly chooses observations from majority class which are eliminated until the data set gets balanced. Informative undersampling follows a pre-specified selection criterion to remove the observations from majority class.
-
OverSampling: This method works with minority class. It replicates the observations from minority class to balance the data. It is also known as upsampling. Random oversampling balances the data by randomly oversampling the minority class. Informative oversampling uses a pre-specified criterion and synthetically generates minority class observations.
-
Synthetic Data Generation or Cost Sensitive Learning (CSL): Instead of replicating and adding the observations from the minority class, it overcome imbalances by generates artificial data. It is also a type of oversampling technique. In regards to synthetic data generation, synthetic minority oversampling technique (SMOTE) is a powerful and widely used method. SMOTE algorithm creates artificial data based on feature space (rather than data space) similarities from minority samples.
Definition:
Forecasting Formula
Forecasting the next point The forecasting formula is the basic equation:
S_t+1 = α y_t+(1−α)S_t, 0<α≤1,t>0.
In other words, the new forecast is the old one plus an adjustment for the error that occurred in the last forecast.
Example:
The table below shows the movement of the price of a commodity over 12 months.
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Price | 25 | 30 | 32 | 33 | 32 | 31 | 30 | 29 | 28 | 28 | 29 | 31 |
- Calculate a 6 month moving average for each month. What is the forecast for month 13?
- Apply exponential smoothing with smoothing constants of 0.7 and 0.8 to derive forecasts for month 13.
Definition:
The betweenness of a vertex v in a graph G := (V, E) with V vertices is computed as follows:
-
For each pair of vertices (s, t), compute the shortest paths between them.
-
For each pair of vertices (s, t), determine the fraction of shortest paths that pass through the vertex in question (here, vertex v).
-
Sum this fraction over all pairs of vertices (s, t).
-
More compactly the betweenness can be represented as:
- where σst is total number of shortest paths from node s to node t and σst(v) is the number of those paths that pass through v.
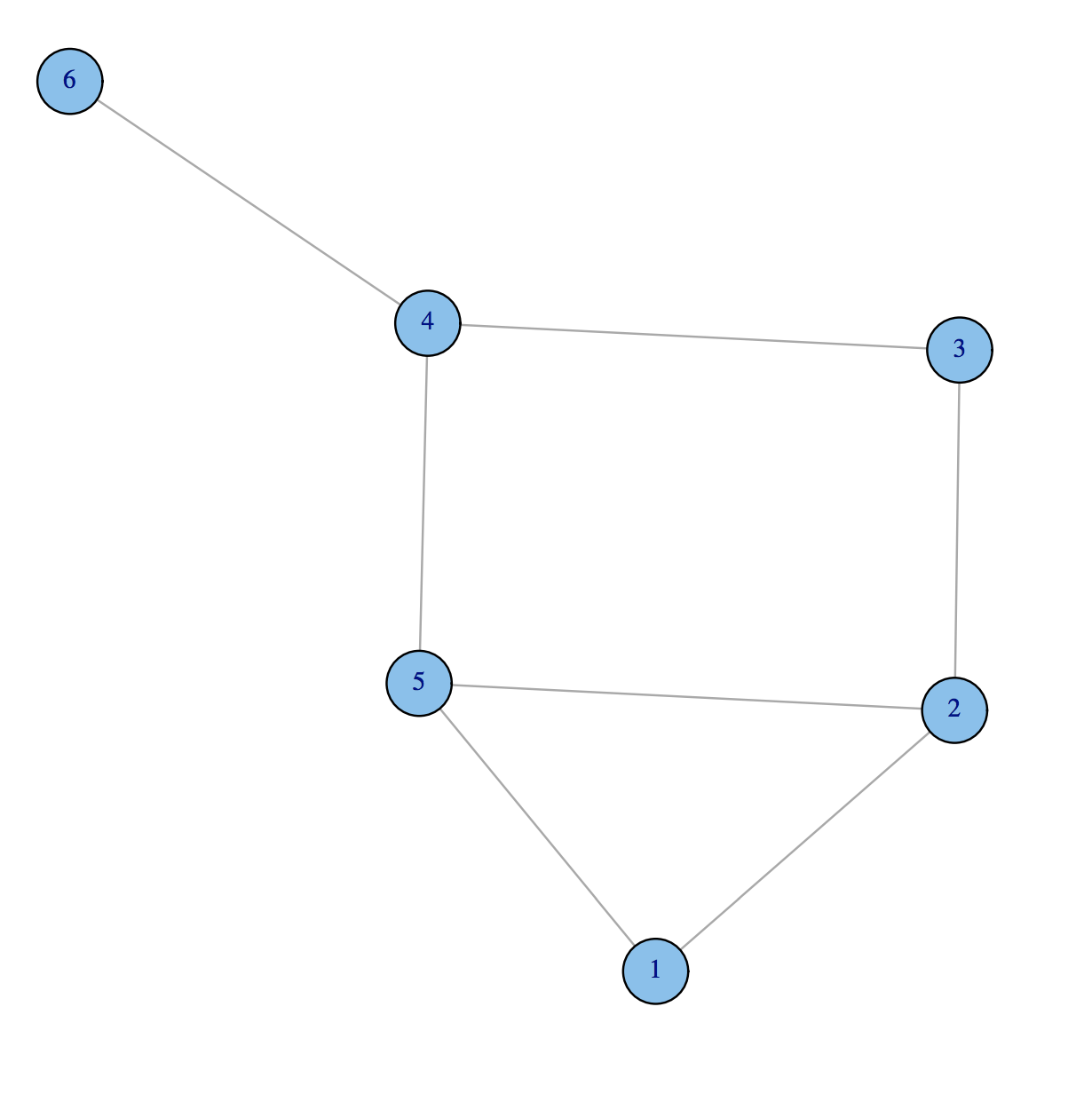
Example: