Integer programming expresses the optimization of a linear function subject to a set of linear constraints over integer variables.
Integer programming is the class of problems that can be expressed as the optimization of a linear function subject to a set of linear constraints over integer variables. It is in fact NP-hard. More important, perhaps, is the fact that the integer programs that can be solved to provable optimality in reasonable time are much smaller in size than their linear programming counterparts.
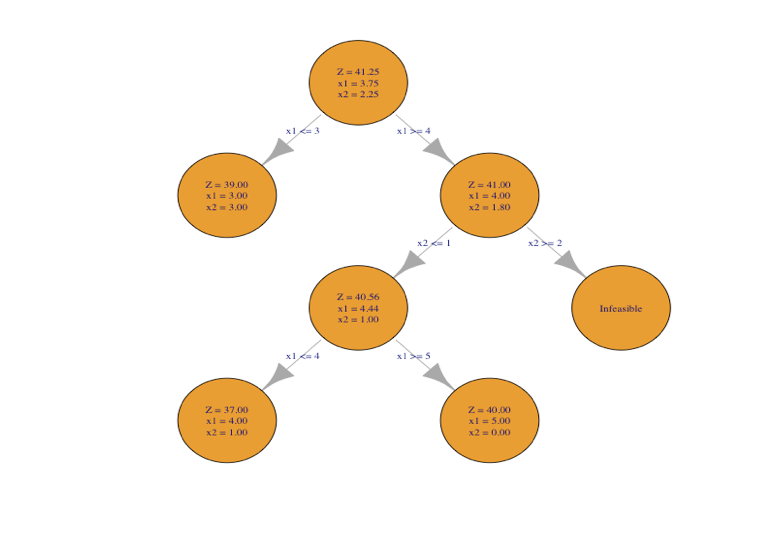
By using the branch and bound algorithm which is a divide an conquer algorithm. We break down a integer programming problem into smaller pieces and then find the optimal solution for each smaller piece to we arrive at the best one.
Given the integer programming problem of the form
max: 8 x1 + 5 x2;
s.t
x1 + x2 <= 6;
9 x1 + 5 x2 <= 45;
int: x1, x2
The algorithm written will solve the problem and then output a tree graph that facilitates a visual look on how the algorithm works.