/DirectedLouvain

Primary LanguageC++GNU General Public License v2.0GPL-2.0

Directed Louvain algorithm

The algorithm used in this package is based on the Louvain algorithm developed by V. Blondel, J.-L. Guillaume, R. Lambiotte, E. Lefebvre and was downloaded on the Louvain algorithm webpage ([1]). The algorithm was then adjusted to handle directed graphs and to optimize directed modularity of Arenas et al. ([2]). These modifications were mostly made by Anthony perez and by Nicolas Dugué.

The directed modularity is proved to be more efficient in the case of directed graphs as shown in Direction matters in complex networks: A theoretical and applied study for greedy modularity optimization and Directed Louvain : maximizing modularity in directed networks ([3,4]). For any citation of this work please use the following:

@article{DP22,
    author  = {Nicolas Dugué and Anthony Perez},
    title   = {Direction matters in complex networks: A theoretical and applied study for greedy modularity optimization},
    journal = {Physica A: Statistical Mechanics and its Applications},
    volume  = {603},
    pages   = {127798},
    year    = {2022},
    issn    = {0378-4371},
    doi     = {https://doi.org/10.1016/j.physa.2022.127798},
}

How to use

The algorithm works in two steps, namely computing communities and then displaying hierarchical tree. Note that the algorithme computes a hierarchical community structure, with several levels. More information are given below regarding the meaning and use of such levels.

Computing communities

The graph must be in edgelist format, that is one edge per line as follows (the weight being optional):

src dest [weight]

Weighted graphs are automatically recognized by the program and there is no need to specify it in the command line. Moreover, it is mandatory that vertices of the input graph are numbered from 0 to n-1. To ensure a proper computation of the communities, the default computation encompasses a renumbering of the input graph. The option -n indicates that the graph is already numbered from 0 to n-1 and hence avoids renumbering. Important: communities are written using the original label nodes.

The standard command is:

./bin/community -f examples/graph.txt -l -1 -v > graph.tree

Several options are available, among which:

  • -f path to the input graph (edgelist or binary format (.bin))
  • -g value of the resolution parameter: the algorithm favors larger communities if less than 1 and smaller otherwise
  • -n to indicate that the input graph is correctly numbered (from 0 to n-1)
  • -r for reproducibility purposes: the renumbered graph is stored on hard drive.
  • -s for disabling randomness: the algorithm will consider vertices from 0 to n-1

More options and information are provided using ./bin/community

Another possibility is to pass a binary file containing all information regarding the graph. We strongly recommand to generate the binary file using our program in a first place. Using any binary file compatible with our format would of course work (see the load function in the src/graph.cpp file, more information to come).

Graph representation: CSR format

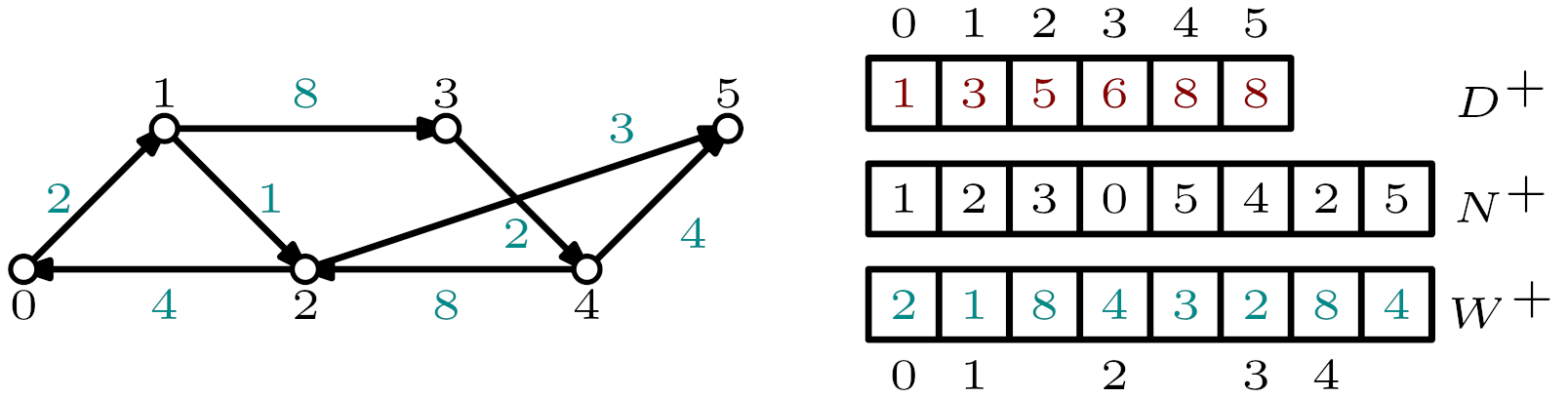
Graphs are stored under the Compressed Sparse Row (CSR) format.
Several structures are containing the whole graph information:

  • two arrays of cumulative degrees (out- and in-degrees): for out-degrees, each index i contains the sum of all out-degrees for nodes from 0 to i.
  • two arrays of outcoming and incoming arcs: the d(0) (out- or in-degree of node 0) first values contain neighbors of node 0 and so on.
    To find the first neighbor of a given node i one simply needs to consider the difference between cumulative degrees of i and i-1.
  • two array of outcoming and incoming weights: similar to the previous ones but store weights instead of node identifiers.

Example of CSR format for a directed graph. The displayed arrays contain information regarding out-neighbors and weighted out--degrees only. CSR example

Examples

Using examples/graph.txt one obtains:

./bin/community -f examples/graph.txt -l -1 -v -r > examples/graph.tree

to compute hierarchical community structure (using original label nodes) by first renumbering the graph, and then writing files for reproducibility. The next runs would thus be:

./bin/community -f examples/graph.txt -l -1 > examples/graph.tree

Another useful value for -l is -2, which computes only the last level of the hierarchical structure. Finally, using an already renumbered graph one gets:

./bin/community -f examples/graph_renum.txt -l -1 -v -n > examples/graph.tree

The program can also start with any given partition using -p option

./bin/community -f examples/graph.txt -p examples/graph.part -v

Improvements

To ensure a faster computation (with a loss of quality), one can use the -q option to specify that the program must stop if the increase of modularity is below epsilon for a given iteration or pass:

./bin/community examples/graph.txt -l -1 -q 0.0001 > examples/graph.tree

Display communities information

The following command displays information on the tree structure (number of hierarchical levels and nodes per level) and is equivalent to using option -l -1:

./bin/hierarchy graph.tree

The following command displays the belonging of nodes to communities for a given level of the tree:

./bin/hierarchy graph.tree -l 2 > graph_node2comm_level2

Using -l -2 displays the last level of the hierarchy.

References