A GPU-accelerated differentiable simulation toolbox for additive manufacturing (AM) based on JAX.
JAX-AM is a collection of several numerical tools, currently including Discrete Element Method (DEM), Computational Fluid Dynamics (CFD), Phase Field Method (PFM) and Finite Element Method (FEM), that cover the analysis of the Process-Structure-Property relationship in AM.
Our vision is to share with the AM community a free, open-source (under the GPL-3.0 License) software that facilitates the relevant computational research. In the JAX ecosystem, we hope to emphasize the potential of JAX for scientific computing. At the same time, AI-enabled research in AM can be made easy with JAX-AM.
🔥 Join us for the development of JAX-AM! 🚀
DEM simulation can be used for simulating powder dynamics in metal AM.
Free falling of 64,000 spherical particles.
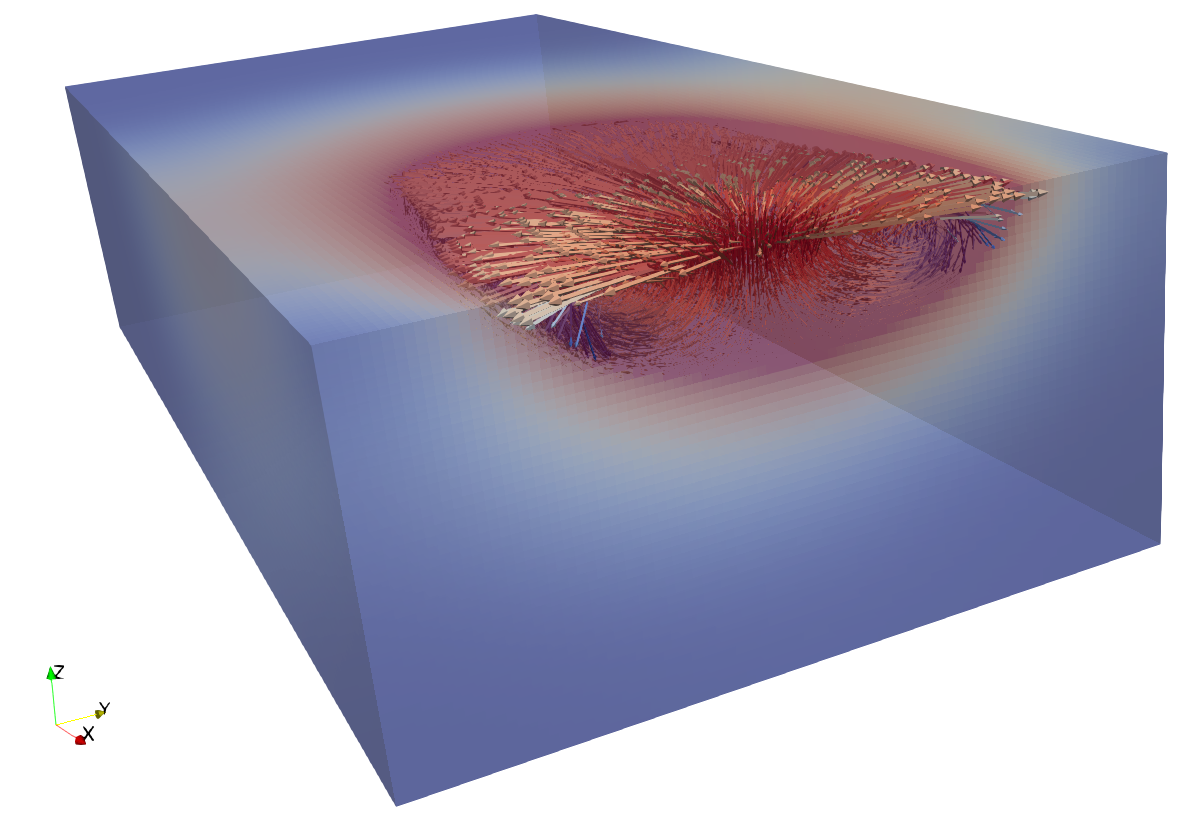
CFD helps to understand the AM process by solving the (incompressible) Navier-Stokes equations for velocity, pressure and temperature.
Melt pool dynamics.
PFM models the grain development that is critical to form the structure of the as-built sample.
Microstructure evolution.
Directional solidification with isotropic (left) and anisotropic (right) grain growth.
FEM is a powerful tool for thermal-mechanical analysis in AM. We support the following features
- 2D quadrilateral/triangle elements
- 3D hexahedron/tetrahedron elements
- First and second order elements
- Dirichlet/Neumann/Cauchy/periodic boundary conditions
- Linear and nonlinear analysis including
- Heat equation
- Linear elasticity
- Hyperelasticity
- Plasticity
- Differentiable simulation for solving inverse/design problems without human deriving sensitivities, e.g.,
- Toplogy optimization
- Optimal thermal control
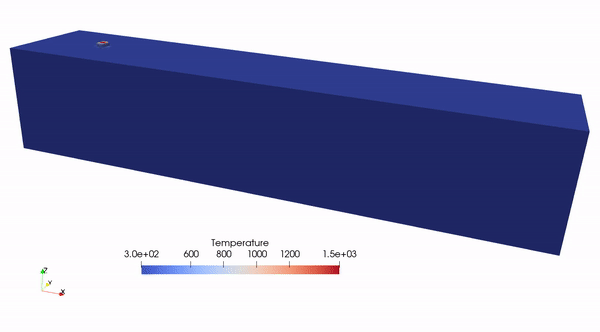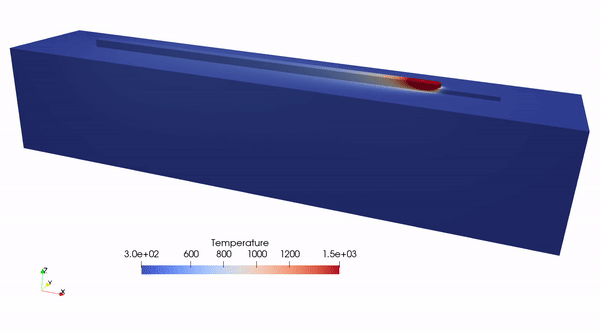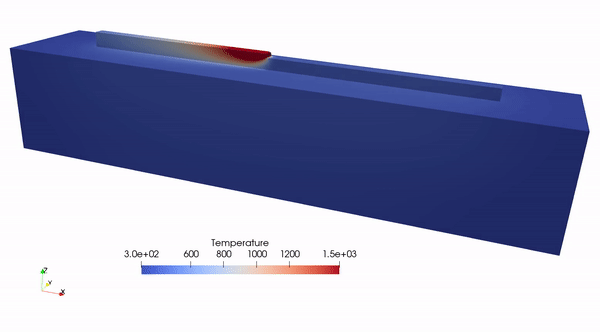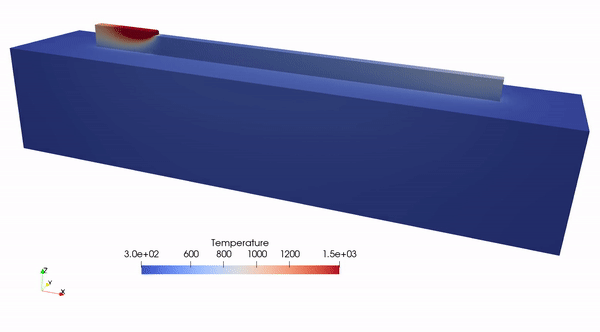
Thermal profile in direct energy deposition.
Linear static analysis of a bracket.
Topology optimization with differentiable simulation.
Please see the web documentation for the installation and use of this project.
This project is licensed under the GNU General Public License v3 - see the LICENSE for details.