This Repository provides two fast implementations of the active CMA-ES algorithm derived from its original Matlab code. Costly matrix operations are mapped on efficient BLAS / MKL code.
There is a native Python implementation based on numpy/scipy and a C++ implementation called via ctypes based on Armadillo. For high dimensional problems (dim >= 100) both implementations perform similar, for low dimensions the C++ version is faster. Only the most commonly used CMA-ES parameters are supported to keep both implementations clean and simple. The Python version supports parallel evaluation of the cost function. Two parallel retry mechanisms are provided, a simple one to analyze the problem and a novel coordinated one for hard optimization problems. For testing and comparison there is an easy to use Python API for four of ESAs space mission design optimization problems ( GTOPToolbox).
Citing Challenges in High-dimensional Reinforcement Learning: "… learning a full covariance matrix introduces non-trivial algorithm internal cost and hence prevents the direct application of CMA-ES to high-dimensional problems". And Nevergrad on CMA: "CMA is excellent for control (e.g. neurocontrol) when the environment is not very noisy (num_workers ~50 ok) and when the budget is large (e.g. 1000 x the dimension)". It seems there is a need for an efficient implementation of the CMA-ES algorithm, not only for reinforcement learning but for general "real world" optimization tasks engineers are faced with. Cost functions associated with these tasks tend to be multi-modal, non-continuous, non-smooth, partially defined and sometimes even non-deterministic which makes CMA-ES the natural choice. The new implementations outperform their stochastic scipy alternatives differential_evolution and dual_annealing significantly for higher dimensions. In combination with a novel coordinated parallel retry mechanism CMA-ES can overcome many of its shortcomings and solve problems which were up to now out of reach for optimization in general.
-
pip install fcmaes -
for C++ version:
-
install Armadillo
-
adapt CMakeLists.txt
-
compile _fcmaescpp and link against a fast BLAS implementation like MKL or OpenBLAS.
-
compile fast-cma-es/_fcmaescpp
-
-
pip install fcmaes -
for C++ version:
-
install Armadillo
-
adapt CMakeLists.txt
-
compile _fcmaescpp and link against a fast BLAS implementation like MKL or OpenBLAS.
-
-
parallel retry will not work because function objects cannot be sent to another process.
-
Linux subsystem for Windows, see Linux subsystem or Ubuntu subsystem. Tested with Ubuntu 18.04, fcmaes performance is about 98% of a native Linux installation. C++ variant and both parallel retry mechanism work.
Usage is very similar to scipy.optimize.minimize.
from fcmaes import cmaes
ret = cmaes.minimize(fun, bounds, x0)
print (ret.x, ret.fun, ret.nfev)fcmaes.cmaes.minimize cannot handle constraints and derivatives (jac, hess, hessp). If the initial guess x0 is undefined, a feasible uniformly distributed random value is automatically generated. It is strongly recommended to define bounds, since CMA-ES uses them also for internal scaling. For multi-modal non-smooth objective functions CMA-ES is usually faster and more reliable than scipy minimize. Additional parameters are
-
popsize(default 31) - Size of the population used. Instead of increasing this parameter for hard problems, it is often better to use parallel retry instead. Reducepopsizefor a narrower search if your budget is restricted. -
input_sigma(default 0.3) - The initial step size. Can be defined for each dimension separately. Both parallel retry mechanism set this parameter together with the initial guess automatically. -
is_parallel(default False) - Calls the objective function for the whole population in parallel. Useful for costly objective functions but is switched off when you use parallel retry.
For the C++ variant use instead:
from fcmaes import cmaescpp
ret = cmaescpp.minimize(fun, bounds, x0)The C++ variant is currently restricted to Linux and requires that a fast BLAS implementation like MKL or OpenBLAS is installed.
For other operating systems you can compile the C++ source acmaesoptimizer.cpp yourself and adapt cmaescpp.py to load the resulting library.
Alternatively there is an ask/tell interface to interact with CMA-ES:
es = cmaes.Cmaes(bounds, x0)
for i in range(iterNum):
xs = es.ask()
ys = [fun(x) for x in xs]
status = es.tell(ys)
if status != 0:
breakFor simple parallel retry use:
from fcmaes.optimizer import logger
from fcmaes import retry
ret = retry.minimize(fun, bounds, logger=logger())For advanced coordinated parallel retry use:
from fcmaes.optimizer import logger
from fcmaes import advretry
ret = advretry.minimize(fun, bounds, logger=logger())Parallel retry does not support an initial quess x0 and initial step size input_sigma because it
uses generated guesses and step size values. Use parameter logger to specify the
log output, default is no logging. Use
fcmaes.optimizer import logger to log both into a file and to stdout.
Check the Tutorial for more details.
You can switch to the C++ variant by setting parameter useCpp to True.
It is possible to use other optimization methods with parallel retry, see
examples.py and
advexamples.py.
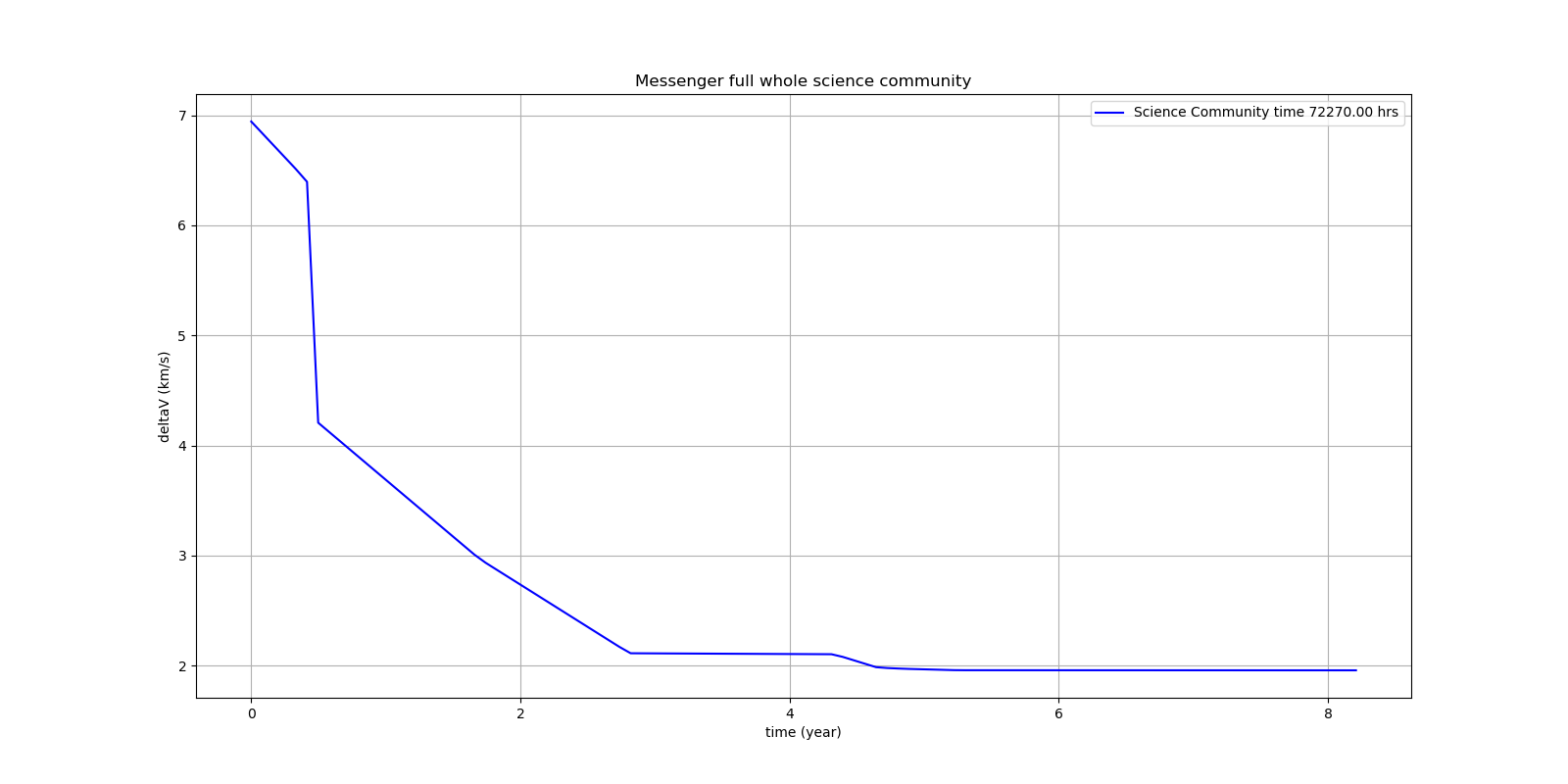
On a single AMD 3950x CPU using Anaconda 2019.10 for Linux the new CMA-ES implementation called by the included parallel coordinated retry mechanism solves ESAs 26-dimensional Messenger full problem in about 2.5 hours on average. The Messenger full benchmark models a multi-gravity assist interplanetary space mission from Earth to Mercury. In 2009 the first good solution (6.9 km/s) was submitted. It took more than five years to reach 1.959 km/s and three more years until 2017 to find the optimum 1.958 km/s. The picture below shows the progress of the whole science community since 2009:
A 100-CPU cluster and about 20x100 CPU hours were required to find 10 solutions near 2.0 km/s, see Midaco. Now you can solve this problem in Python on a single desktop CPU. This means, optimization can be applied to problems previously reserved for search algorithms. CMA-ES and the novel coordinated parallel retry algorithm are in no way designed specifically for space mission design but are generally applicable to all hard optimization problems.
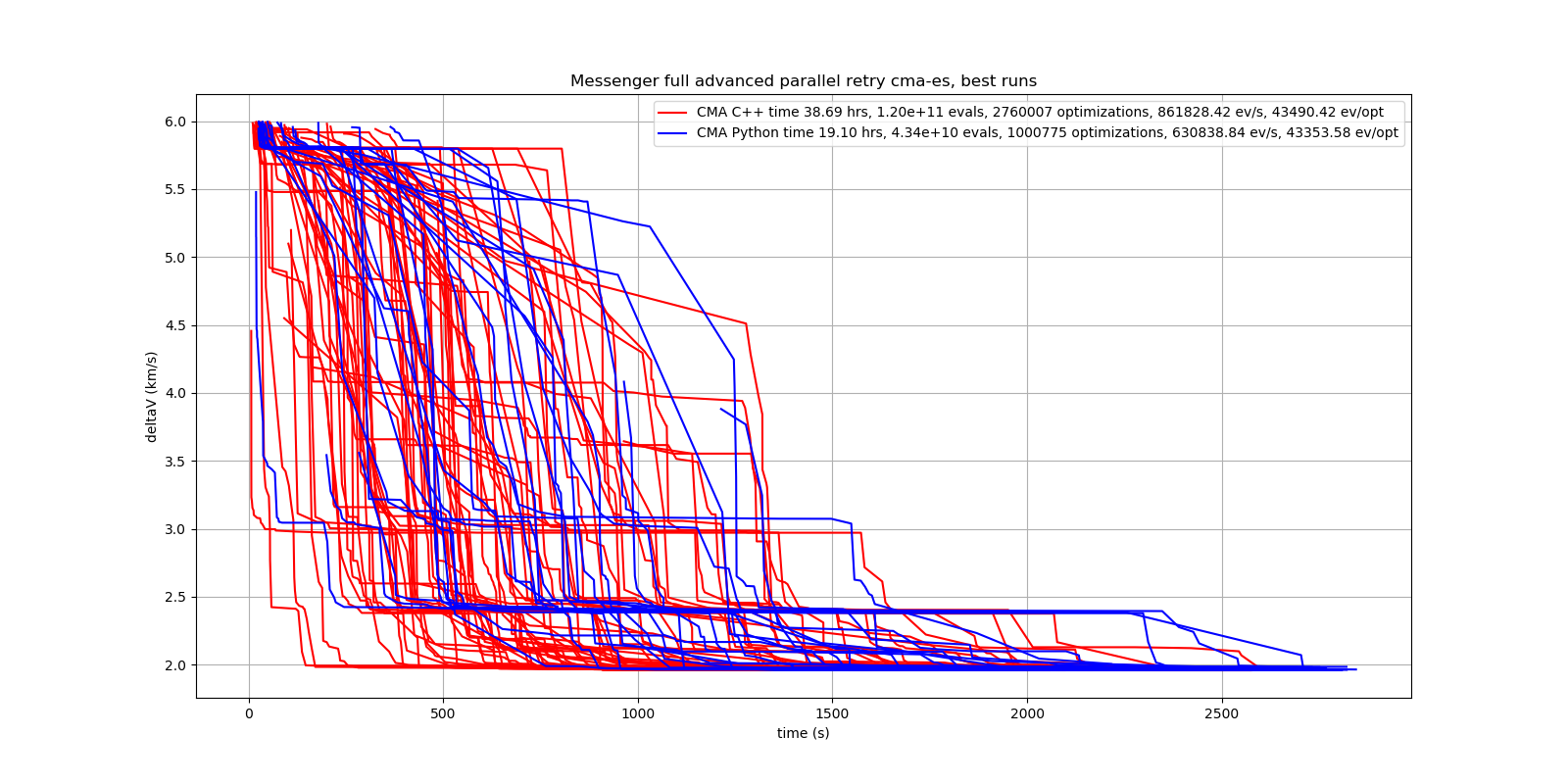
The following picture shows 96 successful CMA-ES advanced retry runs out of 273. All 96 runs, more than a third, produced a result better than 2 km/s, many reached the absolute minimum at 1.958 km/s.
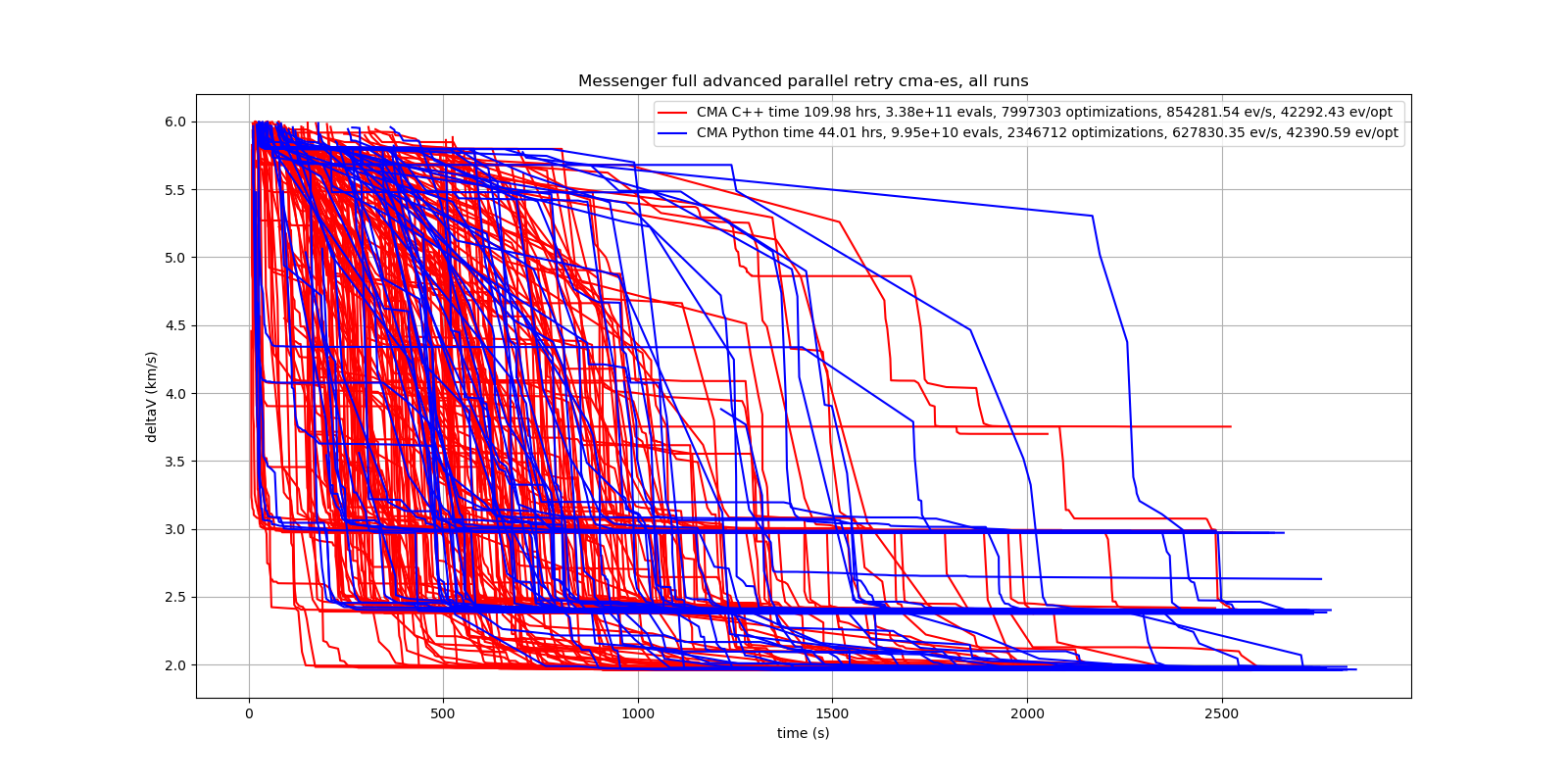
Here are all 273 runs, including the ones reaching local minima at 2.4 and 3.0 km/s.
Using this CMA-ES implementation with parallel retry performs more than 800000 messenger_full evaluations per second on an AMD 3950x processor. About 8-10 times faster than the "official" CMA-ES Python implementation. Both the Python and the C++ variant rely heavily on the configured BLAS library - which defaults to Intel MKL if you use Anaconda .
The log output of the parallel retry contains the following rows:
-
time (in sec)
-
evaluations / sec
-
number of retries - optimization runs
-
total number of evaluations in all retries
-
best value found so far
-
mean of the values found by the retries below the defined threshold
-
standard deviation of the values found by the retries below the defined threshold
-
list of the best 20 function values in the retry store
-
best solution (x-vector) found so far
Mean and standard deviation would be misleading when using advanced retry, because of the retries initiated by crossover. Therefore the rows of the log output differ slightly:
-
time (in sec)
-
evaluations / sec
-
number of retries - optimization runs
-
total number of evaluations in all retries
-
best value found so far
-
worst value in the retry store
-
number of entries in the retry store
-
list of the best 20 function values in the retry store
-
best solution (x-vector) found so far