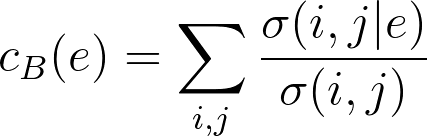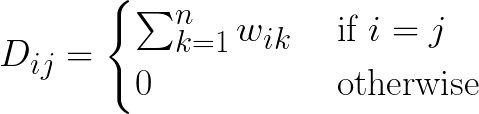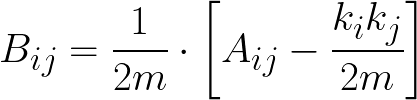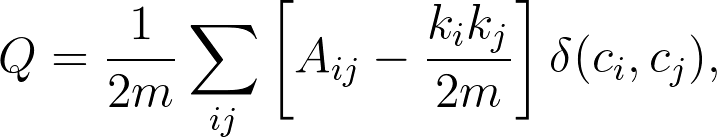communities

communities is a Python library for detecting community structure in graphs. It implements the following algorithms:

Louvain method
Girvan-Newman algorithm
Hierarchical clustering
Spectral clustering
Bron-Kerbosch algorithm

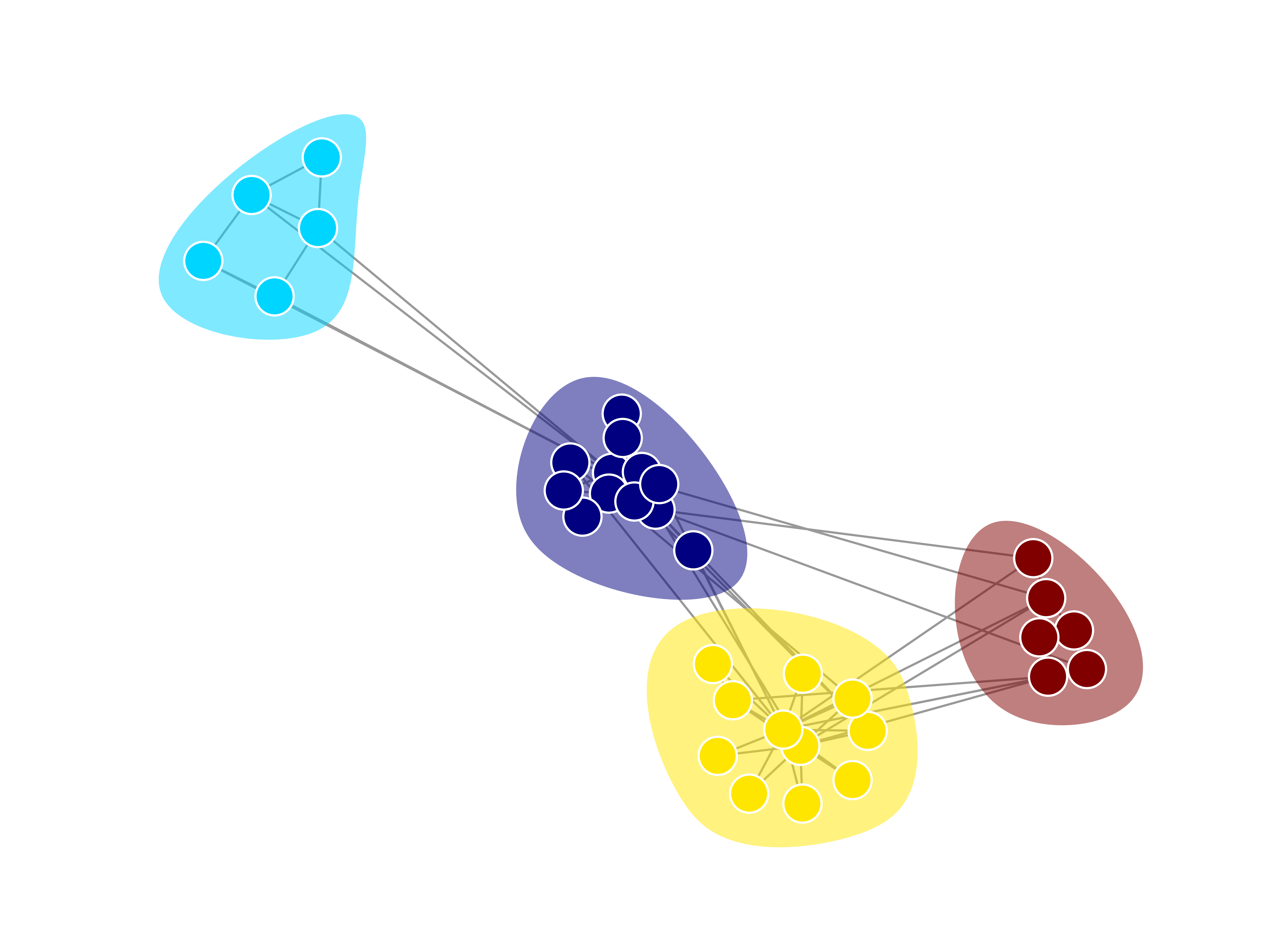
You can also use communities to visualize these algorithms. For example, here's a visualization of the Louvain method applied to the karate club graph:

Installation

communities can be installed with pip:

$ pip install communities

Getting Started

Each algorithm expects an adjacency matrix representing an undirected graph, which can be weighted or unweighted. This matrix should be a 2D numpy array. Once you have this, simply import the algorithm you want to use from communities.algorithms and plug in the matrix, like so:

import numpy as np
from communities.algorithms import louvain_method

adj_matrix = np.array([[0, 1, 1, 0, 0, 0],
                       [1, 0, 1, 0, 0, 0],
                       [1, 1, 0, 1, 0, 0],
                       [0, 0, 1, 0, 1, 1],
                       [0, 0, 0, 1, 0, 1],
                       [0, 0, 0, 1, 1, 0]])
communities, _ = louvain_method(adj_matrix)
# >>> [{0, 1, 2}, {3, 4, 5}]

The output of each algorithm is a list of communities, where each community is a set of nodes. Each node is referred to by the index of its row in the adjacency matrix.

Some algorithms, like louvain_method and girvan_newman, will return two values: the list of communities and data to plug into a visualization algorithm. More on this in the Visualization section.

Algorithms

Louvain's Method

louvain_method(adj_matrix : numpy.ndarray, n : int = None) -> list

Implementation of the Louvain method, from Fast unfolding of communities in large networks. This algorithm does a greedy search for the communities that maximize the modularity of the graph. A graph is said to be modular if it has a high density of intra-community edges and a low density of inter-community edges.

Louvain's method runs in O(nᆞlog²n) time, where n is the number of nodes in the graph.

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of your graph
n (int or None, optional (default=None)): Terminates the search once this number of communities is detected; if None, then the algorithm will behave normally and terminate once modularity is maximized

Example Usage:

from communities.algorithms import louvain_method

adj_matrix = [...]
communities, _ = louvain_method(adj_matrix)

Girvan-Newman algorithm

girvan_newman(adj_matrix : numpy.ndarray, n : int = None) -> list

Implementation of the Girvan-Newman algorithm, from Community structure in social and biological networks. This algorithm iteratively removes edges to create more connected components. Each component is considered a community, and the algorithm stops removing edges when no more gains in modularity can be made. Edges with the highest betweenness centralities (i.e. those that lie between many pairs of nodes) are removed. Formally, edge betweenness centrality is defined as:

where

σ(i,j) is the number of shortest paths from node i to j
σ(i,j|e) is the number of shortest paths that pass through edge e

The Girvan-Newman algorithm runs in O(m²n) time, where m is the number of edges in the graph and n is the number of nodes.

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of your graph
- If your graph is weighted, then the weights need to be transformed into distances, since that's how they'll be interpreted when searching for shortest paths. One way to do this is to simply take the inverse of each weight.
n (int or None, optional (default=None)): Terminates the search once this number of communities is detected; if None, then the algorithm will behave normally and terminate once modularity is maximized

Example Usage:

from communities.algorithms import girvan_newman

adj_matrix = [...]
communities, _ = girvan_newman(adj_matrix)

Hierarchical clustering

hierarchical_clustering(adj_matrix : numpy.ndarray, metric : str = "cosine", linkage : str = "single", n : int = None) -> list

Implementation of a bottom-up, hierarchical clustering algorithm. Each node starts in its own community. Then, the most similar pairs of communities are merged as the hierarchy is built up. Communities are merged until no further gains in modularity can be made.

There are multiple schemes for measuring the similarity between two communities, C₁ and C₂:

Single-linkage: min({sim(i, j) | i ∊ C₁, j ∊ C₂})
Complete-linkage: max({sim(i, j) | i ∊ C₁, j ∊ C₂})
Mean-linkage: mean({sim(i, j) | i ∊ C₁, j ∊ C₂})

where sim(i, j) is the similarity between nodes i and j, defined as either the cosine similarity or inverse Euclidean distance between their row vectors in the adjacency matrix, A_i and A_j.

This algorithm runs in O(n³) time, where n is the number of nodes in the graph.

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of your graph
metric (str, optional (default="cosine")): Scheme for measuring node similarity; options are "cosine", for cosine similarity, or "euclidean", for inverse Euclidean distance
linkage (str, optional (default="single")): Scheme for measuring community similarity; options are "single", "complete", and "mean"
n (int or None, optional (default=None)): Terminates the search once this number of communities is detected; if None, then the algorithm will behave normally and terminate once modularity is maximized

Example Usage:

from communities.algorithms import hierarchical_clustering

adj_matrix = [...]
communities = hierarchical_clustering(adj_matrix, metric="euclidean", linkage="complete")

Spectral clustering

spectral_clustering(adj_matrix : numpy.ndarray, k : int) -> list

Implementation of a spectral clustering algorithm. This type of algorithm assumes the eigenvalues of the adjacency matrix hold information about community structure. Here's how it works:

Compute the Laplacian matrix, L = D - A, where A is the adjacency matrix and D is the diagonal matrix
Compute the k smallest eigenvectors of L, skipping the first eigenvector
Create a matrix V containing eigenvectors v₁, v₂, ... v_n as columns
Cluster the rows in V using k-means into k communities

This algorithm is NP-hard.

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of your graph
k (int): Number of communities to cluster nodes into

Example Usage:

from communities.algorithms import spectral_clustering

adj_matrix = [...]
communities = spectral_clustering(adj_matrix, k=5)

Bron-Kerbosch algorithm

bron_kerbosch(adj_matrix : numpy.ndarray, pivot : bool = False) -> list

Implementation of the Bron-Kerbosch algorithm for maximal clique detection. A maximal clique in a graph is a subset of nodes that forms a complete graph and would no longer be complete if any other node was added to the subset. Treating maximal cliques as communities is reasonable, as cliques are the most densely connected groups of nodes in a graph. Because a node can be a member of more than one clique, this algorithm will sometimes identify overlapping communities.

If your input graph has less than 3^n/3 maximal cliques, then this algorithm runs in O(3^n/3) time (assuming pivot=True).

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of your graph
- Note that this algorithm treats the graph as unweighted
pivot (bool, optional (default=False)): If True, the pivot variant of the algorithm (described here) will be used
- This will make the algorithm more efficient if your graph has several non-maximal cliques

Example Usage:

from communities.algorithms import bron_kerbosch

adj_matrix = [...]
communities = bron_kerbosch(adj_matrix, pivot=True)

Visualization

Plot communities

draw_communities(adj_matrix : numpy.ndarray, communities : list, dark : bool = False, filename : str = None, seed : int = 1)

Visualize your graph such that nodes are grouped into their communities and color-coded.

Returns a matplotlib.axes.Axes representing the plot.

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of your graph
dark (bool, optional (default=False)): If True, the plot will have a dark background and color scheme, else it will have a light color scheme
filename (str or None, optional (default=None)): If you want to save the plot as a PNG, filename is the path of the file to save it as; set to None to display the plot interactively
dpi (int or None, optional (default=None)): Dots per inch (controls the resolution of the image)
seed (int, optional (default=2)): Random seed

Example Usage:

from communities.algorithms import louvain_method
from communities.visualization import draw_communities

adj_matrix = [...]
communities, frames = louvain_method(adj_matrix)

draw_communities(adj_matrix, communities)

Animate the Louvain method

louvain_animation(adj_matrix : numpy.ndarray, frames : list, dark : bool = False, duration : int = 15, filename : str = None, dpi : int = None, seed : int = 2)

Use this to animate the application of the Louvain method to your graph. In this animation, the color of each node represents the community it's assigned to, and nodes in the same community are clustered together. Each step of the animation will show a node changing color (i.e. being assigned to a different community) and being moved to a new cluster, and the corresponding update to the graph's modularity.

This function returns a matplotlib.animation.FuncAnimation object representing the animation.

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of your graph
frames (list): List of dictionaries representing each iteration of the algorithm
- Each dictionary has two keys: "C", which holds a node-to-community lookup table, and "Q", the modularity value of the graph
- This list of dictionaries is the second return value of the louvain_method
dark (bool, optional (default=False)): If True, the animation will have a dark background and color scheme, else it will have a light color scheme
duration (int, optional (default=15)): The desired duration of the animation in seconds
filename (str or None, optional (default=None)): If you want to save the animation as a GIF, filename is the path of the file to save it as; set to None to display the animation as an interactive plot
dpi (int or None, optional (default=None)): Dots per inch (controls the resolution of the animation)
seed (int, optional (default=2)): Random seed

Example Usage:

from communities.algorithms import louvain_method
from communities.visualization import louvain_animation

adj_matrix = [...]
communities, frames = louvain_method(adj_matrix)

louvain_animation(adj_matrix, frames)

Utilities

Inter-community adjacency matrix

intercommunity_matrix(adj_matrix : numpy.ndarray, communities : list, aggr : Callable = sum) -> numpy.ndarray

Creates an inter-community adjacency matrix. Each node in this matrix represents a community in communities, and each edge between nodes i and j is created by aggregating (e.g. summing) the weights of edges between nodes in communities[i] and nodes in communities[j].

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of the graph from which communities were extracted
communities (list): List of communities
aggr (Callable, optional (default=sum)): Function that takes a list of inter-community edge weights and combines them into a single edge weight

Example Usage:

from statistics import mean
from communities.algorithms import louvain_method
from communities.utilities import intercommunity_matrix

adj_matrix = [...]
communities = louvain_method(adj_matrix)
intercomm_adj_matrix = intercommunity_matrix(adj_matrix, communities, mean)

Graph Laplacian

laplacian_matrix(adj_matrix : numpy.ndarray) -> numpy.ndarray

Computes the graph Laplacian. This matrix is used in the spectral_clustering algorithm, and is generally useful for revealing properties of a graph. It is defined as L = D - A, where A is the adjacency matrix of the graph, and D is the degree matrix, defined as:

where w_ik is the edge weight between a node i and its neighbor k.

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of your graph

Example Usage:

from communities.utilities import laplacian_matrix

adj_matrix = [...]
L = laplacian_matrix(adj_matrix)

Modularity matrix

modularity_matrix(adj_matrix : numpy.ndarray) -> numpy.ndarray

Computes the modularity matrix for a graph. The modularity matrix is defined as:

where

A_ij is the weight of the edge between nodes i and j
k_i and k_j are the sum of the weights of the edges attached to nodes i and j, respectively
m is the sum of all of the edge weights in the graph

Parameters:

adj_matrix (numpy.ndarray): Adjacency matrix representation of your graph

Modularity

modularity(mod_matrix : numpy.ndarray, communities : list) -> float

Computes modularity of a partitioned graph. Modularity is defined as:

where

A_ij is the weight of the edge between nodes i and j
k_i and k_j are the sum of the weights of the edges attached to nodes i and j, respectively
m is the sum of all of the edge weights in the graph
c_i and c_j are the communities of the nodes
δ is the Kronecker delta function (δ(x, y) = 1 if x = y, 0 otherwise)

Parameters:

mod_matrix (numpy.ndarray): Modularity matrix computed from the adjacency matrix representation of your graph
communities (list): List of (non-overlapping) communities identified in the graph

Example Usage:

from communities.algorithms import louvain_method
from communities.utilities import modularity_matrix, modularity

adj_matrix = [...]
communities = louvain_method(adj_matrix)

mod_matrix = modularity_matrix(adj_matrix)
Q = modularity(mod_matrix, communities)

nnnnnice/communities

communities

Installation

Getting Started

Algorithms

Louvain's Method

Girvan-Newman algorithm

Hierarchical clustering

Spectral clustering

Bron-Kerbosch algorithm

Visualization

Plot communities

Animate the Louvain method

Utilities

Inter-community adjacency matrix

Graph Laplacian

Modularity matrix

Modularity