vasco: discover hidden correlations in your data

vasco is a Postgres extension that helps you discover hidden correlations in your data. It is based on the MINE family of statistics.

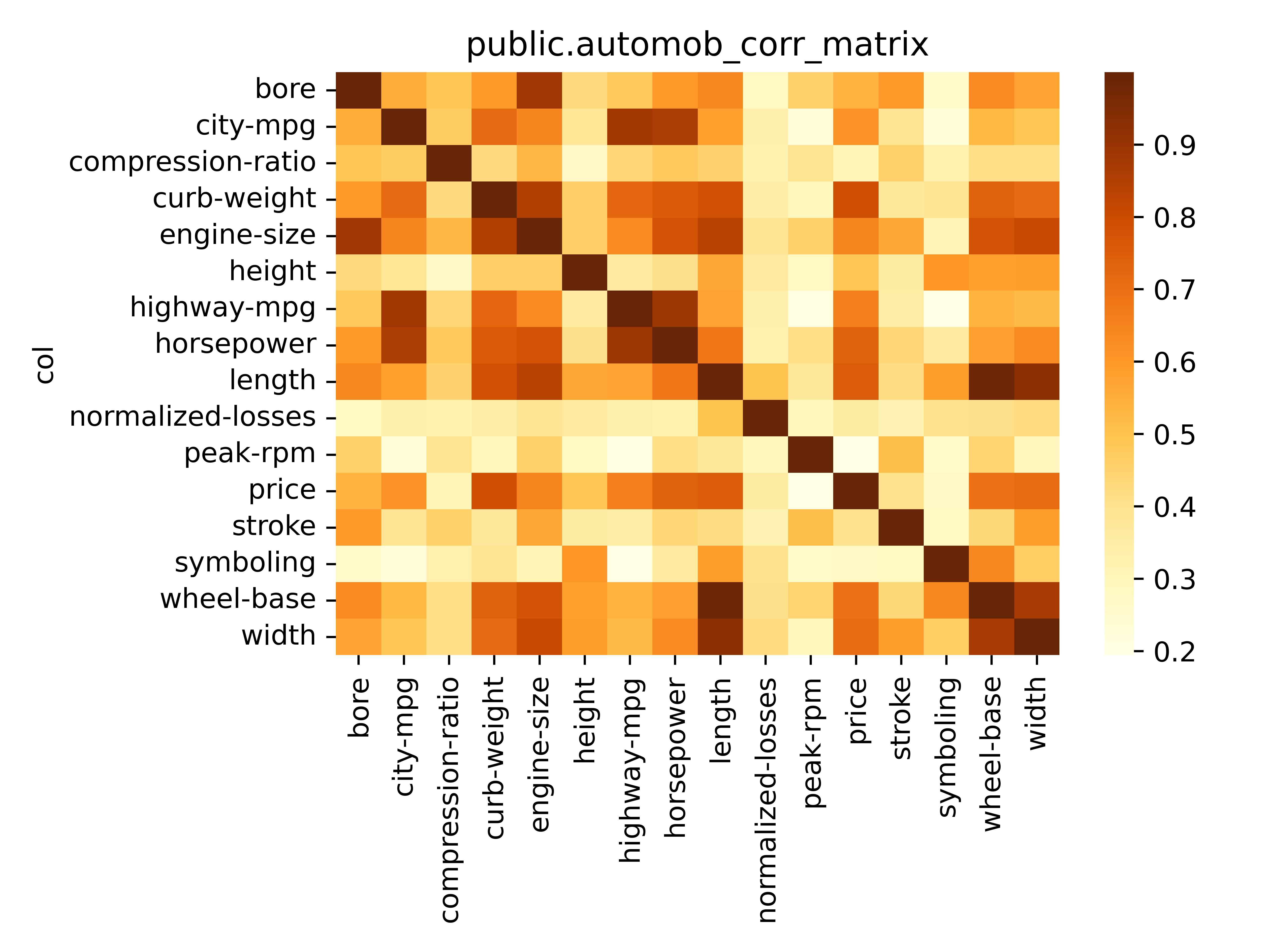
Using the Automobile dataset found in demo/data as an example.

SELECT vasco_corr_matrix('vasco_demo."Automobile_data"', 'auto_corr_matrix')

vasco will explore the table Automobile_data for correlations between its columns pairs. A symmetric matrix of these correlations will be stored in the table auto_corr_matrix. You can use that table for BI and analytics.

You can also use the utility script below to plot a heatmap of that matrix.

./scripts/plot_corr_matrix.py 'public.auto_corr_matrix'

The main workhorse behind vasco is the MIC [Reshef2011]: an information theory-based measure of association that can capture a wide range of functional and non-functional relationships between variables.

MIC(X,Y) is symmetric and normalized score into a range [0, 1]. A high MIC value suggests a dependency between the investigated variables, whereas MIC=0 describes the relationship between two independent variables.

Table of contents

Installation
Usage
How it works
Next Steps
Thanks
Resources

Installation

cd /tmp
git clone git@github.com:Florents-Tselai/vasco.git
cd vasco
make all # WITH_PGVECTOR=1 to enable pgvector support
make install # may need sudo

Then in a Postgres session run

CREATE EXTENSION vasco

Usage

vasco exposes a set of Postgres functions to compute MINE statistics between two series (X,Y) . In Postgres terms X and X can be arrays, vectors or columns.

Thus, each score function is available in three flavors: using Postgres arrays as argument f(float8[], float8[]), , pgvector vectors f(vector, vector) or columns (hence f is an aggregate function). Necessary MINE parameters can be set as GUC , (prefixed as vasco.*)

Let's discuss the supported statistics and their interpretation. Start by creating a sample dataset

SET extra_float_digits = 0;

CREATE TABLE vasco_data
AS (SELECT RANDOM()                          AS rand_x,
           RANDOM()                          AS rand_y,
           x                                 AS x,
           x                                 AS ident,
           4 * pow(x, 3) + pow(x, 2) - 4 * x AS cubic,
           COS(12 * PI() + x * (1 + x))      AS periodic
    FROM GENERATE_SERIES(0, 1, 0.001) x);

Exploring a table

Th generic approach is the following.

SELECT * FROM vasco_explore('my_schema.my_table')

This will explore the relationships between all possible column pairs in the table and return a detailed table of the results. Including all MINE statistics and additional metadata.

Coming up: an option to reduce the set of columns to consider.

Exploring association strength

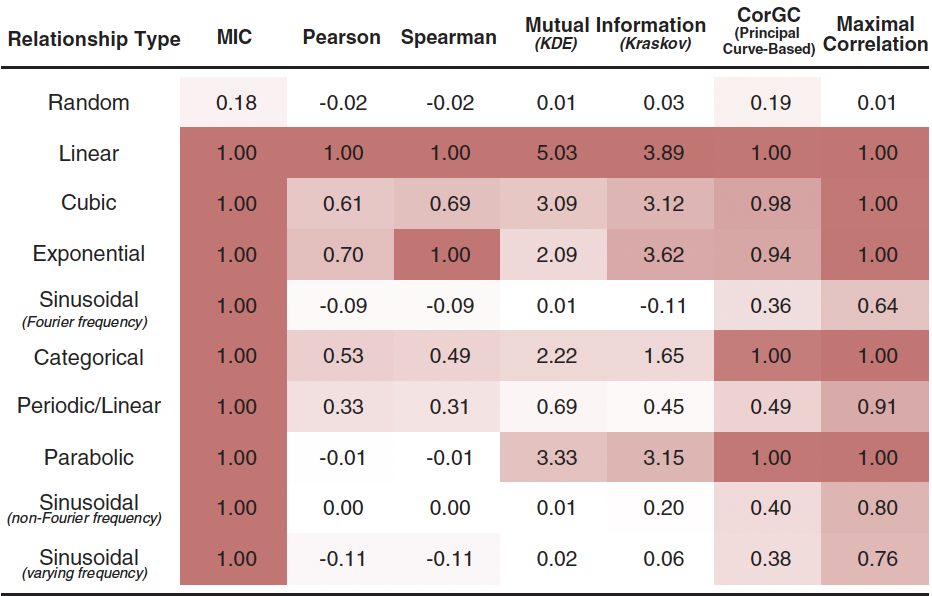
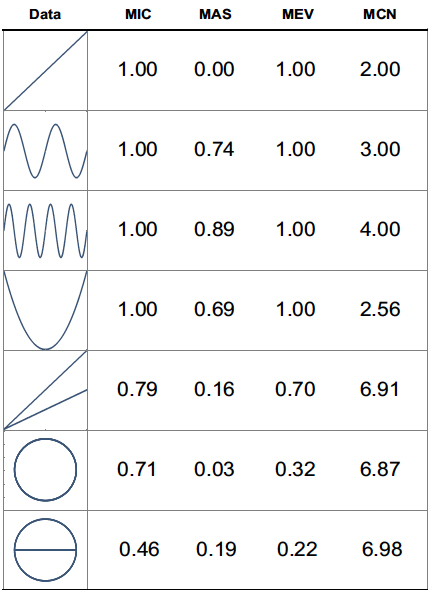
The Maximal Information Coefficient (MIC) measures how strong is the association.

SELECT mic(rand_x, rand_y), -- 0.13 approaching to 0 as sample grows (random independent variables)
       mic(x, ident),       -- 1 identity function hence easy to estimate even with a small sample size
       mic(x, cubic),       -- 0.999 approaching to 1 as sample grows
       mic(x, periodic)     -- 1.
FROM vasco_data;

Exploring the nature of the association

No algorithm can magically detect the function of the relationship between two variables, but MINE statistics can shed some light into the nature of that relationship.

The Maximum Asymmetry Score (MAS) measures how much the relationship deviates from monotonicity.

SELECT mas(X, Y)

The Maximum Edge Value (MEV) measures the degree to which the dataset appears to be sampled from a continuous function.

SELECT mev(X, Y)

The Minimum Cell Number (MCN) measures the complexity of the association.

SET vasco.mine_mcn_eps = 0.0 -- default
SELECT mcn(X, Y)

The Minimum Cell Number General (MCNG) returns the MCN with eps = 1 - MIC .

SELECT mcn_general(X, Y)

The Total Information Coefficient (TIC) .

SET vasco.mine_tic_norm = true -- normalized or not (default = true)
SELECT tic(X, Y)

The Generalized Mean Information Coefficient (GMIC) , a generalization of MIC which incorporates a tuning parameter that can be used to modify the complexity of the association favored by the measure [Luedtke2013] .

SET vasco.mine_gmic_p = 0.0
SELECT gmic(X, Y)

Choosing an estimator

There have been proposed a number of algorithms to estimate the MIC. Currently in vasco you can choose between ApproxMIC from [Reshef2011] or MIC_e from [Reshef2016] .

SET vasco.mic_estimator = ApproxMIC
SET vasco.mic_estimator = MIC_e

pgvector support

vasco can be build with pgvector support .

In that case all MINE statistics can be computed between vector types too.

SELECT mic(  ARRAY [0,1.3,2,0,1.3,20,1.3,20,1.3,20,1.3,20,1.3,2]::float4[]::vector,
             ARRAY [0,1.3,2,0,1.3,20,1.3,20,1.3,20,1.3,20,1.3,2]::float4[]::vector
         )

Configuration parameters

The following MINE parameters can be set via GUC.

vasco.mine_c
vasco.mine_alpha
vasco.mic_estimator
vasco.mine_mcn_eps
vasco.mine_tic_norm
vasco.mine_gmic_p

How it works

As described in [Reshef2011] :

The maximal information coefficient (MIC) is a measure of two-variable dependence designed specifically for rapid exploration of many-dimensional data sets. MIC is part of a larger family of maximal information-based nonparametric exploration (MINE) statistics, which can be used not only to identify important relationships in data sets but also to characterize them.

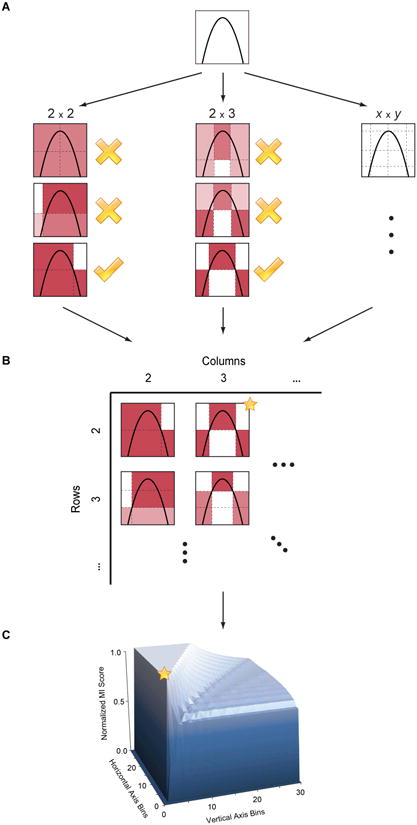
Intuitively, MIC is based on the idea that if a relationship exists between two variables, then a grid can be drawn on the scatterplot of the two variables that partitions the data to encapsulate that relationship.

Thus, to calculate the MIC of a set of two-variable data, we explore all grids up to a maximal grid resolution, dependent on the sample size computing for every pair of integers (x,y) the largest possible mutual information achievable by any x-by-y grid applied to the data. We then normalize these mutual information values to ensure a fair comparison between grids of different dimensions and to obtain modified values between 0 and 1.

These different combination of grids form the so-called characteristic matrix M(x,y) of the data. Each element (x,y) of M stores the highest normalized mutual information achieved by any x-by-y grid. Computing M is the core of the algorithmic process and is computationally expensive. The maximum of M is the MIC and the rest of MINE statistics are derived from that matrix as well.

TL;DR: Computing the Characteristic Matrix is the big deal; Once that is done, computing the statistics is trivial.

Next Steps

Try out ChiMIC [Chen2013] and BackMIC [Cao2021]:
Currently M is re-computed every time a function score is called. That's a huge waste of resources. Caching M or sharing it between runs should be the first optimization to be done.
A potential next step would be continuously updating the CM as columns are updated (think a trigger or bgw process).
Make an extension for SQLite and DuckDB as well
Build convenience functions to create variable pairs and explore tables in one pass.

Thanks

For MINE statistics, vasco currently uses the implementation provided by [Albanese2013] via the minepy package.

Alternative implementations are coming up.

Resources

[Reshef2011]

(1, 2, 3) Reshef, D. N., Reshef, Y. A., Finucane, H. K., Grossman, S. R., McVean, G., Turnbaugh, P. J., ... & Sabeti, P. C. (2011). Detecting novel associations in large data sets. science, 334(6062), 1518-1524.

[Albanese2013]

Albanese, D., Filosi, M., Visintainer, R., Riccadonna, S., Jurman, G., & Furlanello, C. (2013). Minerva and minepy: a C engine for the MINE suite and its R, Python and MATLAB wrappers. Bioinformatics, 29(3), 407-408.

[Luedtke2013]

Luedtke A., Tran L. The Generalized Mean Information Coefficient https://doi.org/10.48550/arXiv.1308.5712

[Chen2013]

Chen Y, Zeng Y, Luo F, Yuan Z. 2016 A new algorithm to optimize maximal information coefficient. PLoS ONE 11, e0157567. (doi:10. 1371/journal.pone.0157567) GitHub

[Zhang2014]

Zhang Y, Jia S, Huang H, Qiu J, Zhou C. 2014 A novel algorithm for the precise calculation of the maximal information coefficient. Sci. Rep.-UK 4, 6662. (doi:10.1038/ srep06662) http://lxy.depart.hebust.edu.cn/SGMIC/SGMIC.htm

[Ge2016]

Ge, R., Zhou, M., Luo, Y. et al. McTwo: a two-step feature selection algorithm based on maximal information coefficient. BMC Bioinformatics 17, 142 (2016). https://doi.org/10.1186/s12859-016-0990-0

[Reshef2016]

Yakir A. Reshef, David N. Reshef, Hilary K. Finucane and Pardis C. Sabeti and Michael Mitzenmacher. Measuring Dependence Powerfully and Equitably. Journal of Machine Learning Research, 2016. PDF

[Xu2016]

Xu, Z., Xuan, J., Liu, J., & Cui, X. (2016, March). MICHAC: Defect prediction via feature selection based on maximal information coefficient with hierarchical agglomerative clustering. In 2016 IEEE 23rd International Conference on Software Analysis, Evolution, and Reengineering (SANER) (Vol. 1, pp. 370-381). IEEE. http://cstar.whu.edu.cn/paper/saner_16.pdf

[Matejka2017]

Matejka and G. Fitzmaurice. Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing. ACM SIGCHI Conference on Human Factors in Computing Systems, 2017.

[Albanese2018]

Davide Albanese, Samantha Riccadonna, Claudio Donati, Pietro Franceschi; A practical tool for Maximal Information Coefficient analysis, GigaScience, giy032, https://doi.org/10.1093/gigascience/giy032

[Cao2021]

Cao, D., Chen, Y., Chen, J., Zhang, H., & Yuan, Z. (2021). An improved algorithm for the maximal information coefficient and its application. Royal Society open science, 8(2), 201424. PDF GitHub

[Shao2021]

Shao, F. & Liu, H. (2021). The Theoretical and Experimental Analysis of the Maximal Information Coefficient Approximate Algorithm. Journal of Systems Science and Information, 9(1), 95-104. https://doi.org/10.21078/JSSI-2021-095-10

noahgarcia5550/vasco

vasco: discover hidden correlations in your data