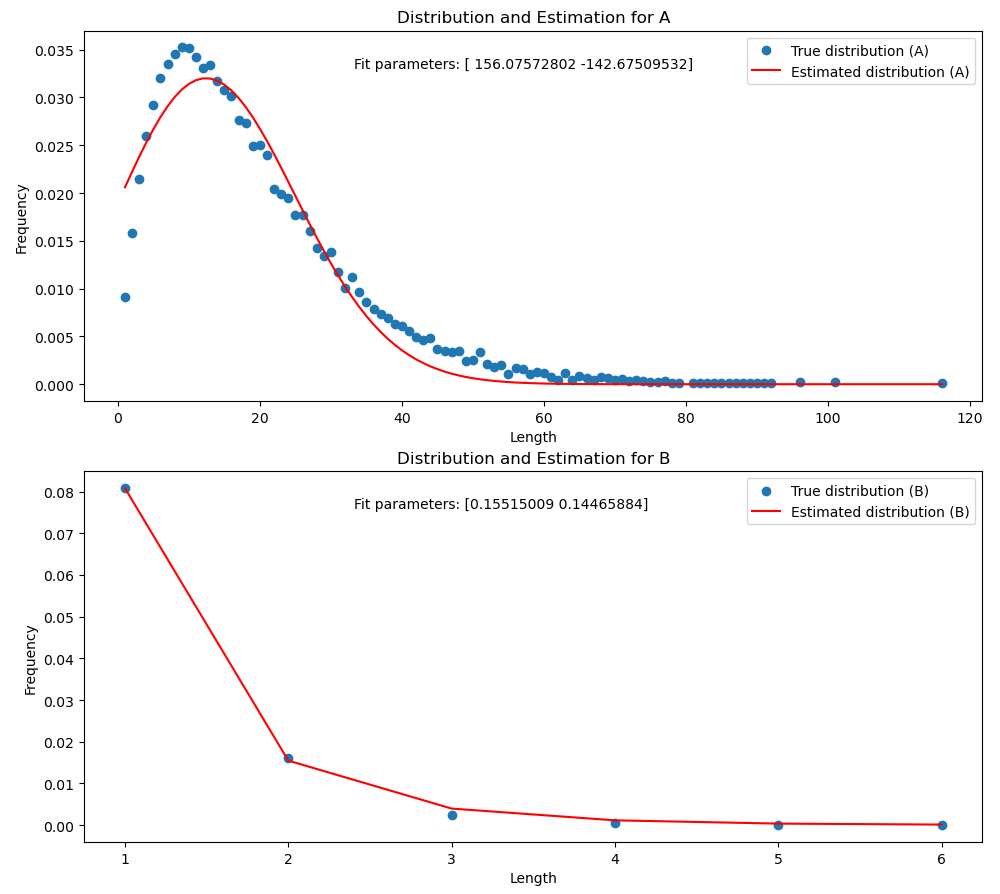
See: markov_chain_polymer_sampling.py
This Python script simulates the length of homogen (only one type of monomer) parts of a polymer using a Markov chain model. It generates a trajectory of monomer sequences and computes the length distribution of subsequences containing the same monomer. The script also estimates the distribution of the subsequences using a (in this case gamma) distribution and plots the true and estimated distributions.
- Set the simulation parameters such as the number of steps, states (monomers), and transition matrix in the script.
- Run the script to simulate the Markov chain and generate a polymer trajectory.
- The script computes the length distribution of homogen subsequences for each monomer.
- A gamma distribution is fitted to the true length distributions.
- The true and estimated length distributions are plotted using Matplotlib.
See: polymer_subswapping.py
This generates a sequence consisting of alternating 'BXBX...', with 'X' randomly populated by either 'A' or 'B' based on the given probabilities.
The trivial case populates 'X' with 'A' or 'B' (1/0) creates alternating sequence of 'ABAB', and so on, meaning that both appear in chains of length 1 with a probability of 0.5.
- NumPy
- Matplotlib
- Scipy
To run the script with default parameters, simply execute:
python3 markov_chain_polymer_sampling.pyThis will generate a polymer trajectory using the specified Markov chain model, compute the length distribution of homogen subsequences, fit a gamma distribution to the true length distribution, and plot the true and estimated distributions.