Fall, 2020 -- Raziel Carvajal-Gómez and Peter Van Roy
The main objective of this project is the implementation and evaluation of a gossip-based algorithm using the message-passing model in Erlang. Concretely, in this project you will:
- Deploy a network of Erlang process;
- Implement and deploy the gossip-based Peer Sampling (PS) service;
- Analyze and report the convergence behavior of this service.
The PS service is a decentralized gossip-based algorithm. In a nutshell, this service delivers an unbiased-random subset of peers from the whole network, nodes might gossip with. This is done via periodic exchanges of neighboring peers between two nodes.
💡 Recall. The term peer as well as node will be used indistinctly in the rest of this text to represent one participant in the network.
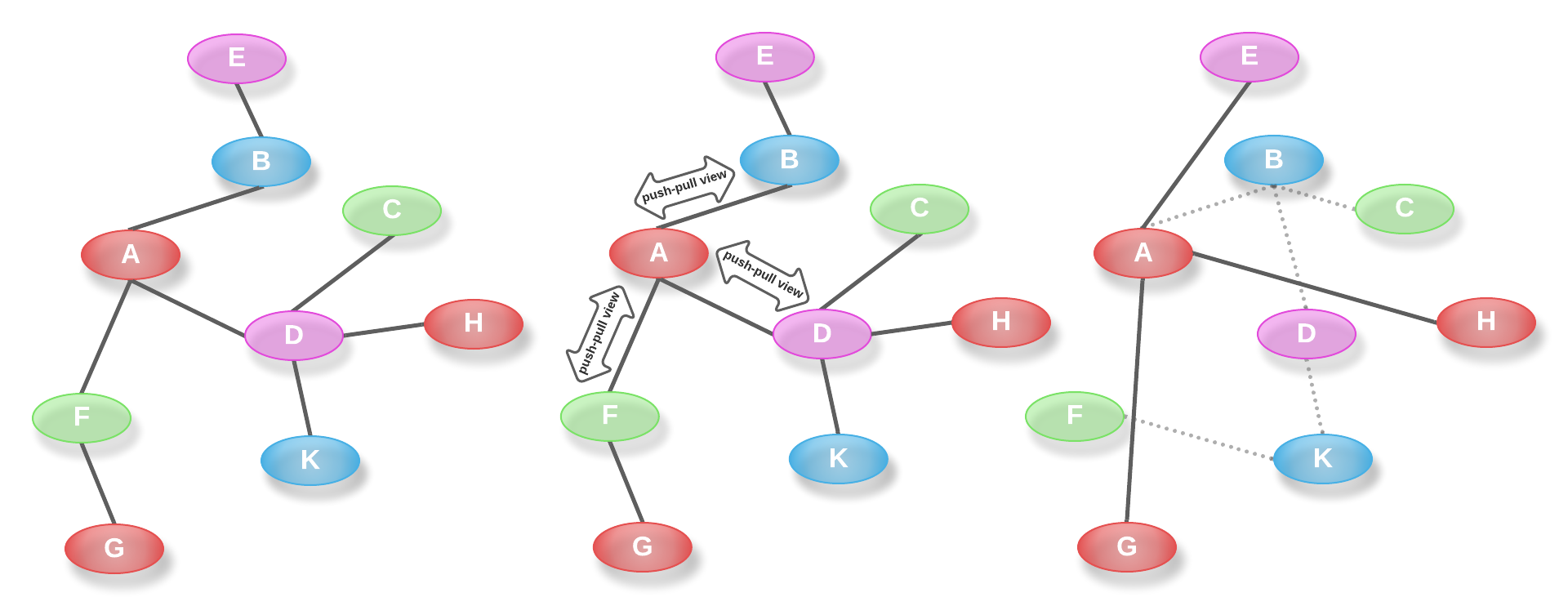
Several distributed algorithms rely on the PS service, it is also relatively easy to conceive other services thanks to this gossip algorithm. For instance, a decentralized social network may rely on the PS service to discover users (peers) following similar interests to form social groups. To do so, users in this social network fetch periodically some other peers from its local instance of the PS service and they keep only those that follow the topics the social group discusses. The figure below depicts three snapshots of a network where every peer runs an instance of the PS service to find social groups interested in similar topics; circles represent peers and colors represent topics.
Initially, peer A has some neighboring nodes however any of these neighbors are colored in red. Hence, the red social group contains A as its only member. After three iterations (exchanges with peers F, D and B), the PS service delivers a different set of A's neighbors to find out peers colored in red (H and G). In the third snapshot, A has discovered new nodes to grow the social group of red peers.
💡 Notice that an iteration of the PS service results in changing the underlying topology of the whole social network. The network topology is also referred to as an overlay, which represents an undirected graph where peers are vertex and links are defined with the neighboring relation; i. e., if peer X has peer Y in its list of neighbors, then there is an undirected link between X and Y in the overlay.
In this project, we ask you to form a team of two students to complete the following tasks.
- Deploy a network of connected peers;
- Provide an implementation of the PS service;
- Deploy a scenario that allows you to analyze the convergence behavior of the PS service;
- Write down your conclusions in a brief report.
🌴 Relax. You will find more details about the previous requirements in this section.
It is mandatory to use Erlang to complete the previous tasks of development, this will allow you to instantiate a lightweight peer as an Erlang process to have a network of several peers on your laptop.
It is also mandatory to deliver your project as a GitHub repository. It is strongly recommended to fork the current repository, your forked copy should be a private repository, work on the implementation in your local copy and deliver the report as a Markdown file. This will allow you to work more effectively with your teammate as well as pulling the solutions to the exercises for learning Erlang, you will see (or have seen already) in the practical sessions.
The PS service requires a connected network to bootstrap. We say that a network is connected when there exists at least a path between any two pairs of nodes. A simple way to form a network with such characteristics is relying on two well-known data structures: a double-linked list or a binary tree.
💡 Notice that in the case of a double-linked list, every node has at most two neighboring peers, and at most three neighbors in the case of a balanced binary tree.
To deploy the PS service it will be enough to use one of both data structures as a connected network to bootstrap the service. We strongly encourage you to follow these steps to deploy such a network.
- Once you chose either the double-linked list or the binary tree, provide an implementation of this data structure in a server process.
- This server process should expose an API with at least two requests:
- add(Node) adds a node to the data structure;
- getNeighbors(Node) gets the list of neighboring peers of a node.
- Implement a sequential procedure (in bash or any other programming language) that instantiates an Erlang process (peer) and invokes the call add(Node).
- 💡 Notice that this sequential procedure should wait until the last peer has been added to the data structure before every peer start the PS service.
As simple as that, you have a first connected network to initiate the PS service in every peer.
💡 Recall that every peer in the network should have a non-empty set of peers, or simply known as view, to start the active thread (infinite loop) of the PS service. You will get such a view invoking the call getNeighbors(Node). Additionally, you need to assign a unique identifier to every node (with an integer should be enough).
You will find the implementation of the PS service in [Jelasity M. et al 2007], recall that in a previous practical session you were asked to read that article (journal version). If you haven't done so, read until the second section (where you will find the implementation) and we also recommend you read sections 4 and 4.1.
Your implementation should be parametrized to deploy the service in any combination of the following policies:
- Peer selection. The neighbor to gossip with will be chosen at random among all peers in the view (the so call rand selection) or the chosen neighbor will be the one with the highest age (tail selection);
- View propagation. Either every peer sends its local view (push propagation) or exchanges its view with the one of its neighbor (push-pull propagation);
- View selection. When an exchange of views between two peers takes place, the resulted view will contain the most recent entries (healer selection), redundancy of descriptors (swapper selection), or a mixed selection (keeps some recent descriptors with a certain redundancy).
- 💡 Notice that this selection is tweaked based on the self-healing parameter H or the swapper parameter S.
Having a parametrized PS service is essential to deploy and evaluate the convergence behavior of it. One of the main advantages of using Erlang is that your final implementation will look very similar to the pseudo-code shown in [Jelasity M. et al 2007], allowing you to have the first validation of your code by merely comparing that the operations in your implementation take place in the same order as shown in the pseudo-code. The correctness of your implementation will be assessed within several scenarios, discussed in the next section.
The recommended number of peers in the network should be at most 128. You will assess your implementation in an elastic scenario that lets peers join the network, then it makes certain nodes to crash. This scenario also contains a final phase where nodes recover and create an instance of the PS service for a second time. Your deployment should follow, in order, the following timeline.
- ⭕ Bootstrapping phase. Initially, only 40% of the peers start the service using the view from the first connected network (topology formed using a double-linked list or a binary tree);
- 📶 Growing the network. At a pace of every 30 cycles, 20% of the remaining peers will join the network until all nodes (100%) are part of this network;
- 💥 Time to crash. When the lifetime of the PS service has reached 120 cycles, 60% of the peers will crash. To mimic a more realistic scenario, that amount of peers should be chosen randomly;
- ❄️ Back to business (recovery phase). After 30 cycles more, you will choose arbitrarily one alive peer P from the network. To test how the PS service behaves during a phase of recovery, 60% of faulty nodes will join again the network with one condition: every node will have a view with only the descriptor of P;
- 🏁 Halt now. The scenario should stop when 180 cycles have been reached.
This elastic scenario should be deployed twice using the push-pull policy to propagate the peer's view. In the first deployment, you should use the healer policy and the swapper policy in the second deployment, to select peer descriptors.
We recommend to use 3s per cycle in the active thread and fix the maximum size for the peer's view to 7 descriptors. Based on the previous values, the healer policy to select descriptors should set H to 4 and S to 3 as well as H to 3 and S to 4 in the swapper policy.
You need to create a dataset that describes the timeline of a peer per experimental scenario. We recommend you to keep a record with the peer's local data within the active thread of the PS algorithm, just before the timer of this thread has started. You should keep (at least) a tuple with three entries: i) the cycle number of the PS service, ii) the peer identifier and iii) the peer's view. Notice that the peer's view should be a list of peer descriptors where each descriptor will have the neighbor identifier and its age.
Analyzing how a distributed algorithm behaves is not an easy task. [Jelasity M. et al 2007] propose to study several properties of the dynamic graph formed with the network of peers running the PS service. You will analyze only one of these properties, the in-degree.
💡 Recall. In graph theory, the in-degree of a vertex v is the total number of any other vertex that has an edge with v.
In our context, the in-degree of a peer P at a certain cycle of the PS service is the number of nodes in the whole network that contains P in their views. Notice that you can easily compute the in-degree per cycle once you have all the records (logs) from the deployment of one scenario.
Your first task will be to depict the in-degree of both deployments (healer and swapper) in a box plot. You should plot the in-degree of the whole network every 20 cycles. In other words, the requested plot should contain two curves where each curve shows 9 boxes (one box every 20 cycles for a total of 180 cycles).
Finally, you should write your conclusions in a brief report explaining your plot based on the experimental scenario and the parametrization of the PS service.
You will find below every criterion we will use to grade the project, their weights as well as a check-list of elements every criterion should contain to grant you the highest note.
-
Criteria 1 (20%): Deployment of bootstrap network.
- The procedure explaining how nodes join the first network has a clear description;
- The implementation of the double-linked list or binary tree has brief documentation;
- There exists a unit test to confirm the correctness of the chosen data structure to represent the first connected network;
- Double-linked list. Having the add operation is enough;
- Binary tree. Ideally, the binary tree should be balanced.
-
Criteria 2 (50%): PS service implementation.
- The sources contains comments justifying lines-of-code difficult to understand;
- The implementation is fully parametrized;
- The polices of view selection and view selection are consistent with the parametrization;
- The peer descriptors contain an age (integer);
- The code handles exceptions to avoid stopping the active thread;
- The data in the logs is sufficient to compute the in-degree of the peer sampling overlay.
-
Criteria 3 (30%): Deployment of experimental scenario (s) and conclusions.
- The sources to set up the timeline of the experimental scenario contains clear (but brief) documentation;
- The procedure to compute the in-degree is correct and contains brief documentation;
- There is a box plot containing two curves, the first one represent the execution of the healer policy of view selection and the second one represents the swapper policy;
- The execution lasts at least 180 cycles and there is a data point every 20 cycles for the in-degree;
- There is a clear justification of the behavior of curves in the in-degree box plot according to the scenario.