Redução de dimensionalidade

Ao se trabalhar com Machine Learning, podemos nos deparar com modelos com um grande número de atributos. E geralmente é isso que ocorre com datasets do mundo real. Para isso, pode ser necessário a redução de dimensionalidade para ganho de eficiência computacional, ou até para visualizar o resultado na forma de um gráfico. Duas técnicas comuns para isso são o PCA e o t-SNE.

PCA (Principal Component Analysis)

É definido como um método linear não-paramétrico para redução de dimensionalidade em problemas de aprendizado não supervisionado

A ideia do PCA é reduzir a dimensionalidade perdendo o mínimo de informação. Ele busca, então, manter o máximo possível da variabilidade presente no dataset original. Para isso, são criadas novas variáveis a partir das features originais, que são ordenadas de acordo com quanto de variação cada uma consegue explicar. Esses novos componentes criados são completamente não relacionados (ou seja, são ortogonais entre si).

O primeiro componente apresenta a maior variação, seguido do segundo, e assim por diante. Desse modo, como poucos componentes retêm a maior parte da explicação da variação, é possível visualizar e sintetizar as características de datasets com dimensões altas em um espaço de mais baixa dimensão.

O PCA busca preservar a estrutura global do dataset formando clusters bem divididos, mas pode acabar não sendo muito eficiente para preservar as similaridades dentro de um cluster. Além disso, por ser um método linear, trabalha melhor com datasets com características lineares e pode ser útil para achar padrões nesses datasets.

Como funciona?

Na prática, são construídas novas variáveis a partir dos atributos originais, que são uma combinação linear desses atributos.

Uma combinação linear nada mais é do que a representação de um vetor a partir de operações com outros vetores. Assim, dado um conjunto de vetores $v_1, \cdots, v_n$, $v$ será uma combinação linear tal que:

$$ v = a_1v_1 + \cdots + a_nv_n $$

Matemática por trás

Dado um dataset n-dimensional, é computada uma matriz de covariância (também conhecida como matriz de variância-covariância) para todo o conjunto de dados, gerando uma matriz quadrada $n \times n$. Na diagonal é a representação da variância de cada feature, e fora dela são os valores da covariância. Valores positivos indicam uma correlação positiva; valores negativos, uma correlação negativa. Valores próximos ou iguais a 0 significam que as variáveis não são linearmente correlacionadas. O cálculo da covariância é feito para cada ponto do dataset, pela aplicação da fórmula:

$$ COV(x,y) = \dfrac{\sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})}{n-1} $$

Entrando agora um pouco mais na álgebra linear, temos os conceitos de autovalores e autovetores.

Autovetor: vetor cuja direção permanece constante quando uma transformação linear é aplicada a ele ($v$)

Autovalor: indica quanto o vetor irá "encolher" ou "esticar" ao sofrer a transformação ($\lambda$)

Os autovalores podem ser calculados como raízes da seguinte fórmula, onde A é uma matriz quadrada:

$$ det(A-\lambda I) = 0 $$

Para os autovetores relacionados aos autovalores encontrados, basta substituir na fórmula:

$$ Av = \lambda v $$

Aplica-se então essa fórmula, sendo A a nossa matriz de covariância. Os autovetores encontrados formarão os eixos do novo espaço de dimensões. Mas como os autovetores só nos fornecem a direção, precisamos olhar também para os autovalores. Os autovetores com os maiores autovalores são aqueles que fornecem a maior quantidade de informação sobre o dataset.

A ideia é que os autovetores representam o peso de cada variável original sobre cada componente. Já o autovalor é uma indicação direta da importância do componente na explicação da variação total dentro do conjunto de dados.

Para formar a matriz final dos compontentes, então, ordenam-se os autovetores por autovalores decrescentes e escolhem-se k autovetores com os maiores autovalores. A matriz formada (W) tem dimensões $n \times k$, e é usada para transformar os dados para o novo espaço, seguindo:

$$ y = W' \times x $$

Considerações

É necessário tratar valores nulos e normalizar/padronizar as variáveis antes do PCA
Pode não funcionar bem para datasets não lineares

Exemplo de visualização com PCA para 2 componentes Fonte: https://towardsdatascience.com/principal-component-analysis-pca-explained-visually-with-zero-math-1cbf392b9e7d

t-SNE (t-distributed stochastic neighbor embedding)

Método não-linear para redução de dimensionalidade em problemas de aprendizado não supervisionado

Principal objetivo: visualizar os dados numa dimensão mais baixa (geralmente 2D)

Para preservar a estrutura dos dados na dimensão original, é definida uma similaridade condicional entre dois pontos, onde $\left| x_i – x_j\right|$ é a distância euclidiana entre eles e $\left| y_i – y_j\right|$ é a distância entre os pontos já mapeados para a dimensão de destino. Considera-se uma distribuição gaussiana, em torno de $x_i$ com uma determinada variância $\sigma^2_i$:

$$ ⁍ $$

A divisão serve para lidar com cluster com diferentes densidades. É uma espécie de normalização.

Versão simetrizada da similaridade condicional (joint probability condition, ou distribuição de probabilidade conjunta):

$$ ⁍ $$

Com isso, obtemos uma matriz de similaridade para o dataset original, computando a similaridade para cada ponto. Além disso, define-se uma matriz de similaridade também para os pontos mapeados:

$$ q_{ij} = \dfrac{f(|x_i-x_j|)}{\sum\limits_{k\neq i}f(|x_i-x_k|)}, \textnormal{com } f(z) = \dfrac{1}{1+z^2} $$

Aqui, a distribuição muda para t-Student com um grau de liberdade, ou distribuição Cauchy.

O objetivo é que essas matrizes sejam o mais próximas possível. Assim, significa que os pontos do dataset original produzem pontos mapeados similares.

Algoritmo

Tem-se que a similaridade será dada por $|p_{ij} -q_{ij}|$ e a ideia é que se os pontos mapeados estão afastados enquanto os do dataset original estão próximos, eles são atraídos. Do contrário, eles são repelidos. O mapeamento final é obtido quando um equilíbrio é alcançado.

Matematicamente, isso significa minimizar a divergência de Kullback-Leiber entre as duas distribuições ($p_{ij}$ e $q_{ij}$). Essa medida representa a distância entre as duas matrizes de similaridade.

$$ KL(P||Q) = \sum_{i, j} p_{ij} , \log \frac{p_{ij}}{q_{ij}}. $$

Performa-se o gradiente descendente nessa equação, a fim de minimizá-la.

$$ \frac{\partial , KL(P || Q)}{\partial y_i} = 4 \sum_j (p_{ij} – q_{ij}) g\left( \left| x_i – x_j\right| \right) u_{ij} \quad \textrm{onde} , g(z) = \frac{z}{1+z^2}. $$

Por que a distribuição t-Student?

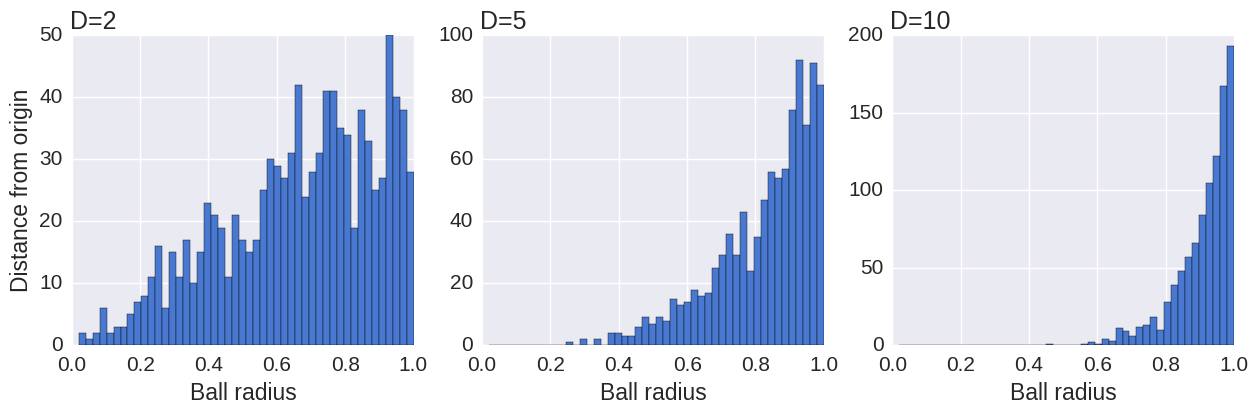
Para um problema usual envolvendo uma bola N-dimensional, o volume dessa bola de raio r escala como $r^N$ (volume de uma n-bola). Quando N é grande, se pegarmos pontos aleatórios da bola uniformemente, a maior porte estará próxima a superfície e poucos estarão próximos do centro.

Se, ao reduzir a dimensionalidade do dataset, usássemos a gaussiana também, teríamos um desbalanceamento na distribuição de distâncias de pontos vizinhos, pois a distribuição de distâncias é muito diferente entre um espaco dimensional alto para um espaço com dimensões menores. Esse desequilíbrio levaria a um excesso das forças de atração, levando a um mapeamento não tão agradável de visualizar.

O que acontece com a distribuição de t-Student com um grau de liberdade (Cauchy) é que a cauda é mais longa que na gaussiana (é uma distribuição de cauda longa/pesada/gorda), o que compensa esse desbalanceamento original.

Então, usando tal distribuição conseguimos visualizações melhores, onde os pontos estão separados de forma mais distinguível.

Existem outras otimizações que podem ser feitas para se obter complexidade $O(N logN)$.

Principais Hiperparâmetros

Alguns relacionados ao processo do gradiente descendente (learning rate, número de iterações, …).

E perplexidade (0-100), que é usado para escolher o desvio padrão $\sigma_i$ da distribuição condicional que representa o dataset original. $\sigma_i$ é definido de maneira que a perplexidade da distribuição condicional $P_i$ se iguala à que foi usada como hiperparâmetro. Uma interpretação seria que a perplexidade é a medida efetiva do número de vizinhos de cada ponto. Perplexidades baixas fazem com que as semelhanças locais dominem as semelhanças num aspecto global. Definindo, por exemplo, uma perplexidade de 30, significa que a atenção do algoritmo será focada em preservar a distância aos 30 vizinhos mais próximos, os pontos restantes quase não serão foco.

Considerações

O tamanho dos clusters não quer dizer nada sobre o tamanho original do dataset, pois o algoritmo expande naturalmente clusters densos e contrai os mais dispersos
As distâncias num plot de t-SNE podem também não dizer nada
Ruído aleatório nem sempre parece ruído aleatório - às vezes ruídos podem ser confundidos com clusters
Pode ser realizado um PCA antes de proceder com o t-SNE, para uma redução inicial de dimensionalidade, pois o t-SNE pode acabar sofrendo da maldição da dimensionalidade.