odow/StochOptFormat

Specification and description of the StochOptFormat file format

StochOptFormat: a data structure for multistage stochastic programming

This repository describes a data structure and file-format for stochastic optimization problems called StochOptFormat, with the file extension .sof.json.

For convenience, we abbreviate StochOptFormat to SOF.

StochOptFormat is defined by the JSON schema https://odow.github.io/StochOptFormat/versions/sof-1.schema.json.

Authors

• Oscar Dowson
• Joaquim Garcia

Contents

• Motivation and design principles
• Example
  • Vocabulary
  • Graphical representation
  • Problem in StochOptFormat
  • Explanation
• Problems, policies, and algorithms
• FAQ
• Implementations
• References

Motivation and design principles

Libraries of benchmark instances have been instrumental in driving progress in many areas of optimization. In stochastic programming, some effort has been made on this front (see, for example, https://www.stoprog.org/resources). However, the predominant file format for these problems, SMPS [4], does not scale to the types of problems we want to solve (large multistage stochastic programs), nor does it permit the variety of problem classes we want to study (for example, stochastic conic programs).

A more recent attempt to standardize a file format for stochastic programming is the stochastic extension to OSiL [3]. StochOptFormat utilizes many of the underlying ideas, but it has enough differences to justify the creation of a new file format. In particular, we use a different standard form for a stochastic program and we do not use XML.

Over the last few years, we (and the broader JuMP team) have set about reimagining how we formulate single period deterministic optimziation problems. The result is a data structure for optimization called MathOptInterface [2]. In addition, we have also set about standardizing how we formulate multistage stochastic programming problems. The result is a natural decomposition of the problem into the policy graph [1].

Those papers present the reasoning of behind many aspects of their design, along with the necessary historical context. However, most of the key ideas can be grasped from the example in the next section. In particular, the example contains all the details required to fully describe a two-stage stochastic linear program. However, you should note that our work naturally extends beyond two-stage to multistage.

MathOptInterface and the policy graph are synergistic with each other. We can use the policy graph to describe the high-level structure of a stochastic program, and we can use MathOptInterface to describe the low-level optimization problem faced by the agent within each node of the policy graphs. Putting these two concepts together leads to a natural data structure for multistage stochastic programs. StochOptFormat is a serialization of this data structure into the JSON file format.

StochOptFormat is inspired by our work on JuMP and SDDP.jl. However, it is not exclusive to Julia or stochastic dual dynamic programming. For example, our format would make it possible to read multistage stochastic programming problems into Python and solve them with the progressive hedging library PySP. We have not implemented the code yet because this is not our area of expertise.

When developing StochOptFormat, we set out to create:

• A format that is able to scale to problems with hundreds of decision periods, state variables, and control variables.
• A format that was defined by a schema, so that files could be validated for syntactic correctness.
• A format that was not restricted to linear programming.
• A format based on the policy graph so that we can go beyond the two-stage realm. Policy graphs allow us to represent a very large class of problem structures, including finite and infinite horizon problems, problems with linear stagewise independence, problems with Markovian structure, and problems represented by an arbitrary scenario tree.
• A well-defined notion of what the solution to a stochastic program is.

Equally as important as the things that we set out to do, are the things that we did not set out to do:

• We did not try to incorporate chance constraints.
• We did not try to incorporate continuous random variables.

Finally, StochOptFormat is not an algebraic modeling language for stochastic programming. Instead, it is an instance format [5].

You should not need to write StochOptFormat files by hand. Nor should you need to consider the exact layout of the file when formulating your model. The analog is the MPS file format. No one writes MPS files by hand, and most people are probably unaware of the exact structure and syntax of an MPS file. Instead, we use high-level algebraic modeling languages like JuMP to build models, and we expect our solvers to handle the difficulty of reading and writing the MPS files.

Example

There are a lot of concepts to unpack in StochOptFormat. We present a two-stage stochastic linear program example first, and then explain each section of the corresponding StochOptFormat file in detail.

Consider a two-stage newsvendor problem. In the first stage, the agent chooses x, the number of newspapers to buy at a cost $1/newspaper. In the second stage, the uncertain demand of d newspapers is realized, and the agent sells u newspapers at a price of $1.50/newspaper, with the constraint that u = min{x, d}. The demand is either 10 units with probability 0.4, or 14 units with probability 0.6.

Vocabulary

Here, we briefly summarize the important terms used by StochOptFormat; we direct the reader to [1] for more information. Note that some of our terms differ slightly from [1]. The act of formalizing a data structure has clarified some of our earlier ideas.

• Nodes

  A policy graph is made up of nodes. Each node corresponds to a point in time at which the agent makes a decision.

  In our example, there are two nodes: first_stage and second_stage.

  For convenience, we also introduce a root node, which is not a node at which the agent makes a decision, but is just used as a marker for where the agent first enters the sequential decision making process. The root node stores the initial value for each state variable (see below).

• Edges

  Edges connect two nodes in the policy graph. Each edge has a from node, a to node, and a probability of transitioning along the edge. Note that the sum of probabilities along outgoing edges of a node does not have to equal 1. This allows, for example, discount factors in cyclic graphs and nodes with no children; see [1] for more details.

  In our example, there are two edges:

  1. root to first_stage with probability 1
  2. first_stage to second_stage with probability 1

• State variables

  State variables are the information in the problem that flows between two nodes along an edge. In each node, each stage variable is associated with an incoming state variable and an outgoing state variable.

  In our example, there is one state variable, x, the number of newspapers purchased in the first stage. The incoming state variable of first_stage represents the initial stock on hand, the outgoing state variable of the first_stage is equivalent to the incoming state variable of the second_stage, and the outgoing state variable of the second_stage is the quantity of unsold newspapers at the end of the second stage.

• Random variables

  Random variables are local to a node, and are assumed to be independent of the incoming state variable and the realization of any prior random variables. Some nodes may not have any random variables. If so, we say that the node is deterministic.

  In our example, the first_stage is deterministic, and the second_stage node has one random variable, d, the demand for newspaper.

• Control variables

  Control variables are decisions taken by the agent within a node. They remain local to the node, and their values are not needed by the agent in future nodes to make a decision.

• Subproblem

  In the policy graph paper [1], the dynamics of the system within each node are split into a transition function, a set of feasible controls, and an objective. Rather than represent these directly in the file format, we find it more convenient to combine these three things in an optimization problem we refer to as the subproblem.

  The subproblem explicitly excludes the cost-to-go terms, so it is not an explicit dynamic programming decomposition. Instead, it is just a structured way of communicating the dynamics of each node.

  In addition, incoming state variables, outgoing state variables, and random variables are all represented by decision variables in the optimization problem. This means that if a random variable is multiplied by a state or control variable in a constraint or in the objective, it is represented in the subproblem as a quadratic objective or constraint, even if the subproblem is linear with the value of the random variable fixed.

  For our example, the first-stage subproblem is:

  max: -1 * x′
  s.t.      x′ >= 0,
  

  and the second-stage subproblem is:

  max: 1.5 * u
  s.t.       u - x     <= 0
             u     - d <= 0
             u         >= 0.
  

Graphical representation

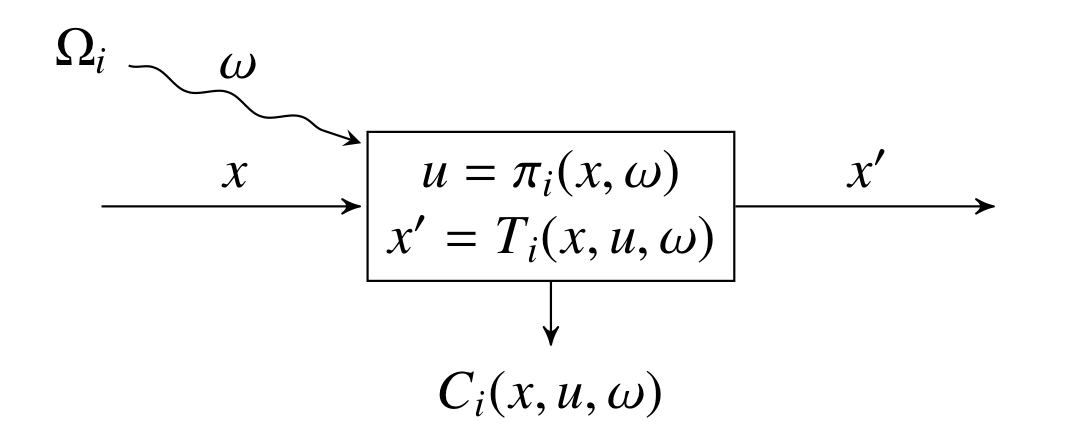
One strength of the policy graph is that the structure can be easily visualized. For each node in the graph, we can draw a picture like the following.

Here, x is the incoming state variable, x' is the outgoing state variable, ω is the random variable observed before making a decision, u is the control variable, Tᵢ is transition function, and Cᵢ is the stage objective. πᵢ is the decision rule, which maps the incoming state variable x and realization of the random variable ω to a feasible control u. (The set of feasible controls u ∈ Uᵢ(x, ω) is not shown.)

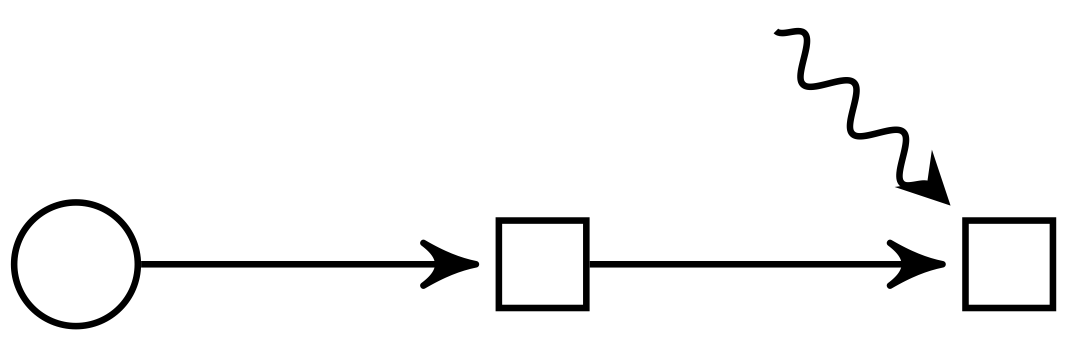
From this basic building block, we can construct an arbitrary policy graph. Our example two-stage stochastic program can be visualized as follows:

Here, the first stage is deterministic, then there is a second stage in which the decision is taken after observing the uncertainty.

We encourage you to read the paper [1] which outlines the full complexity of problems that can be represented, including problems with Markovian structure and infinite horizon problems (that is, cyclic policy graphs).

Problem in StochOptFormat

Encoded in StochOptFormat, the newsvendor problem becomes:

{
  "author": "Oscar Dowson",
  "name": "newsvendor",
  "date": "2023-05-02",
  "description": "A StochOptFormat implementation of the classical two-stage newsvendor problem.",
  "version": {"major": 1, "minor": 0},
  "root": {
    "state_variables": {"x": 0.0},
    "successors": {"first_stage": 1.0}
  },
  "nodes": {
    "first_stage": {
      "subproblem": "first_stage_subproblem",
      "successors": {"second_stage": 1.0}
    },
    "second_stage": {
      "subproblem": "second_stage_subproblem",
      "realizations": [
        {"probability": 0.4, "support": {"d": 10.0}},
        {"probability": 0.6, "support": {"d": 14.0}}
      ]
    }
  },
  "subproblems": {
    "first_stage_subproblem": {
      "state_variables": {
        "x": {"in": "x_in", "out": "x_out"}
      },
      "subproblem": {
        "version": {"major": 1, "minor": 2},
        "variables": [{"name": "x_in"}, {"name": "x_out"}],
        "objective": {
          "sense": "max",
          "function": {
            "type": "ScalarAffineFunction",
            "terms": [{"variable": "x_out", "coefficient": -1.0}],
            "constant": 0.0
          }
        },
        "constraints": [{
          "function": {"type": "Variable", "name": "x_out"},
          "set": {"type": "GreaterThan", "lower": 0.0}
        }]
      }
    },
    "second_stage_subproblem": {
      "state_variables": {
        "x": {"in": "x_in", "out": "x_out"}
      },
      "random_variables": ["d"],
      "subproblem": {
        "version": {"major": 1, "minor": 2},
        "variables": [
          {"name": "x_in"}, {"name": "x_out"}, {"name": "u"}, {"name": "d"}
        ],
        "objective": {
          "sense": "max",
          "function": {
            "type": "ScalarAffineFunction",
            "terms": [{"variable": "u", "coefficient": 1.5}],
            "constant": 0.0
          }
        },
        "constraints": [{
          "function": {
            "type": "ScalarAffineFunction",
            "terms": [
              {"variable": "u", "coefficient": 1.0},
              {"variable": "x_in", "coefficient": -1.0}
            ],
            "constant": 0.0
          },
          "set": {"type": "LessThan", "upper": 0.0}
        }, {
          "function": {
            "type": "ScalarAffineFunction",
            "terms": [
              {"variable": "u", "coefficient": 1.0},
              {"variable": "d", "coefficient": -1.0}
            ],
            "constant": 0.0
          },
          "set": {"type": "LessThan", "upper": 0.0}
        }, {
          "function": {"type": "Variable", "name": "u"},
          "set": {"type": "GreaterThan", "lower": 0.0}
        }]
      }
    }
  },
  "validation_scenarios": [
    [
      {"node": "first_stage"},
      {"node": "second_stage", "support": {"d": 10.0}}
    ], [
      {"node": "first_stage"},
      {"node": "second_stage", "support": {"d": 14.0}}
    ], [
      {"node": "first_stage"},
      {"node": "second_stage", "support": {"d": 9.0}}
    ]
  ]
}

Explanation

A StochOptFormat file is a JSON document. The problem is stored as a single JSON object. JSON objects are key-value mappings enclosed by curly braces.

The file begins with four self-explanatory optional metadata keys: name::String, author::String, date::String, and description::String.

Note: In the following, name::String means that the key of an object is name and the value should be of type String. ::List{Object} means that the type is a List, and elements of the list are Objects.

After the optional metadata keys, there are four required keys:

• version::Object

  An object describing the minimum version of StochOptFormat needed to parse the file. This is included to safeguard against later revisions. It contains two required keys: major and minor. These keys should be interpreted using SemVer.

• root::Object

  An object describing the root node of the policy graph. It has the following required keys:

  • state_variables::Object

    An object describing the state variables in the problem. Each key is the unique name of a state variable. The initial value of the state variable at the root node.

  • successors::Object

    An object in which the keys correspond to nodes and the values correspond to the probability of transitioning from the root node to the key node.

• nodes::Object

  An object mapping the name of each node of the policy graph (excluding the root node) to an object describing the node. Each object has the following required keys:

  • subproblem::String

    The name of the subproblem to use from the subproblems object. Multiple nodes can refer to the same subproblem to reduce redundancy if they share the same structural form.

  • realizations::List{Object} (Optional)

    A list of objects describing the finite discrete realizations of the independent random variable in each node. Each object has two required keys:

    • probability::Number

      The nominal probability of each realization.

    • support::Object

      An object describing the support corresponding to the realization. The keys of the object are the random variables declared in random_variables, and the values are the value of the random variable in that realization.

  • successors::Object (Optional)

    An object in which the keys correspond to nodes and the values correspond to the probability of transitioning from the current node to the key node.

• subproblems::Object

  An object that stores the collection of subproblems in the policy graph. Each object has three required keys:

  • state_variables::Object

    An object that maps the name of each state variable (as defined in the root node) to an object describing the incoming and outgoing state variables in the subproblem. Each object has two required keys:

    • in::String

      The name of the variable representing the incoming state variable in the subproblem.

    • out::String

      The name of the variable representing the outgoing state variable in the subproblem.

  • random_variables::List{String} (Optional)

    A list of strings describing the name of each random variable in the subproblem.

  • subproblem::Object

    The subproblem corresponding to the node as a MathOptFormat object.

There is also an optional key:

• validation_scenarios::List{List{Object}}

  Scenarios to be used to evaluate a policy. validation_scenarios is a list, containing one element for each scenario in the test set. Each element is a list of objects. Each object has two required fields:

  • node::String

    The name of the node to visit.

  • support::Object (Optional)

    The realization of the random variable at that node. Note that support may be an out-of-sample realization, that is, one which is not contained in the corresponding realizations field of the node.

Testing a policy is a larger topic, so we expand on it in the next section, Problems, policies, and algorithms.

Problems, policies, and algorithms

Now that we know how problems are represented in StochOptFormat, we need to introduce some additional vocabulary.

• Problem

  The data structure formulated as a StochOptFormat file. Also called program or model. We standardize on problem.

• Policy

  The solution to a deterministic optimization problem is a vector containing the primal solution for each decision variable, and possibly a second vector containing the dual solution. Both vectors contain a finite number of elements.

  In contrast, the solution to a stochastic program is a policy. A policy is a set of decision rules, with one decision rule for each node in the policy graph. A decision rule is a function which maps the incoming state variable and realization of the random variable at a node to a value for each control variable. This function is typically an infinite dimensional object (since, for example, the state variables can be continuous).

• Algorithm

  An algorithm takes a problem as input and constructs a policy as output. Also called solution method or solver.

Evaluating the policy

Comparing two solutions to a determinstic optimization problem is simple: check the feasibility of each solution, compare objective values, and possibly compare computation time.

In contrast, comparing two policies is not simple. First, a policy produces a distribution of outcomes, so ranking two policies requires a user-provided risk measure based on their risk preference. Moreover, two users may have different risk preferences, so there is no uniquely optimal policy.

Second, in many cases the policy is an infinite dimensional object, and the set of scenarios over which it should be evaluated is so large as to be intractable.

To overcome these two issues, we evaluate the policy by means of an out-of-sample simulation on a finite discrete set of scenarios provided in the validation_scenarios key of a StochOptFormat file.

Solution algorithms should evaluate their policy on each of these scenarios and report the following for each node in each scenario:

• The objective value of the subproblem excluding any cost-to-go terms
• The primal solution for all decision variables in the subproblem
• The dual solution (if one exists) for all constraints in the subproblem.

Solutions should be outputted to a JSON file that conforms to the schema available at https://odow.github.io/StochOptFormat/versions/sof-result.schema.json.

Most notably, the result file must include the SHA-256 checksum of the problem file used to generate the policy to ensure that the two files can be linked.

Evaluating the solution on a finite list of scenarios solves the intractability problem, but it does not solve the user's risk perference problem. However, with the above mentioned report, it is possible to evaluate multiple metrics of the resulting policy, such as expected objective values, and various quantiles.

FAQ

• Q: The policy graph is too complicated. I just want a format for linear T-stage stochastic programs.

  A: For a T-stage problem, our format requires T subproblems, a list of the state variables, and a sequence of edges. Of those things, only the list of edges would be superfluous in a purely T-stage format. So, for the sake of a list of objects like {"node": "1", "probability": 1}, we get a format that trivially extends to infinite horizon problems and problems with a stochastic process that is not stagewise independent.

• Q: Why MathOptFormat instead of LP or MPS files?

  A: MathOptFormat can be read and writen by most programming languages. In addition, it is very general and easy to extend. Please read Section 2 of [2] for more a discussion of the design decisions behind MathOptFormat.

• Q: You don't expect me to write these by hand do you?

  A: No. We expect high-level libraries like SDDP.jl to do the reading and writing for you.

• Q: What happened to SMPS?

  A: SMPS is too limiting for multistage problems.

• Q: This seems catered to SDDP; I just have some scenarios.

  A: The policy graph can represent any scenario tree. For more details read [1].

• Q: I want continuous random variables.

  A: In this initial version of the format, we only consider finite discrete random variables. We might consider adding continuous ones in the future.

• Q: My stochastic process is not stagewise-independent.

  A: Two options: expand the state-space, or create a scenario tree. For more information, read Sections 1, 2, and 3 of [1].

• Q: Where are the risk measures?

  A: Risk measures are not part of the problem. They are another input to the solution algorithm. Put another way, one constructs a risk-averse policy to a problem, rather than finding a policy for a risk-averse problem. In addition many solution algorithms (for example, robust optimization) do not need to consider risk measures.

• Q: I don't like JSON.

  A: We're open to better ideas. JSON has universal support in every major programming language, and is human-readable(-ish). For now, we choose JSON and we will revisit the question if convincing data is presented to show that the approach is not viable.

• Q: JSON seems too verbose.

  A: JSON files compress well. For example, for problems in the MIPLIB 2017 benchmark set, compressed MathOptFormat files are only 19% larger than their compressed MPS equivalents [2].

• Q: I want the uncertainty to be an objective/constraint coefficient.

  A: Formulate the objective/constraint as a ScalarQuadraticFunction. It's up to the reader to infer from the list of the random variables if this is a parameterized ScalarAffineFunction, or a ScalarQuadraticFunction without random variables.

• Q: Follow up to the previous question. I want to have random_variable * x * y.

  A: Changing the quadratic coefficient matrices in solvers is slow, and doing so could easily make the problem non-convex. If you really want to, you could add a slack variable (and equality constraint) z == random_variable * x, and then use z * y. If you are in this case, please open an issue; we would like to see some real-world examples before proceeding further.

• Q: Why haven't you written an interface to ⟨INSERT LANGUAGE HERE⟩ yet?

  A: Does ⟨INSERT LANGUAGE HERE⟩ have a JSON reader? Just import the file!

Implementations

• Pedagogical Python code for solving two-stage stochastic linear programs using Benders decomposition and PuLP is available in the examples directory.

• Pedagogical Julia code for solving two-stage stochastic linear programs using Benders decomposition and JuMP is available in the examples directory.

• Support for reading and writing StochOptFormat files is available in the SDDP.jl libary.

References

[1] Dowson, O. (2020). The policy graph decomposition of multistage stochastic programming problems. Networks, 71(1), 3-23. doi: 10.1002/net.21932 [preprint]

[2] Legat, B., Dowson, O., Garcia, J., Lubin, M. (2022). MathOptInterface: a data structure for mathematical optimization problems. INFORMS Journal on Computing. 34(2), 671–1304. [preprint] [repository]

[3] Fourer, R., Gassmann, H.I., Ma, J. and Martin, R.K. (2009). An XML-based schema for stochastic programs. Ann Oper Res, 166, 313-337. doi: 10.1007/s10479-008-0419-x

[4] Gassmann, H.I. and Kristjánsson, B. (2008). The SMPS format explained. IMA Journal of Management Mathematics, 19(4), 347-377. doi: 10.1093/imaman/dpm007

[5] Gassmann, H.I., Ma, J. and Martin, R.K. (2011). Instance Formats for Mathematical Optimization Models. In Wiley Encyclopedia of Operations Research and Management Science (eds J.J. Cochran, L.A. Cox, P. Keskinocak, J.P. Kharoufeh and J.C. Smith). doi: 10.1002/9780470400531.eorms0411