/WDL_model

Fit a chess Win-Draw-Loss model from played games

Primary LanguagePythonGNU General Public License v3.0GPL-3.0

Generate SF WDL model based on data

Stockfish's "centipawn" evaluation is decoupled from the classical value of a pawn, and is calibrated such that an advantage of "100 centipawns" means the engine has a 50% probability to win from this position in selfplay at move 32 at fishtest LTC time control.
If the option UCI_ShowWDL is enabled, the engine will show Win-Draw-Loss probabilities alongside its "centipawn" evaluation. These probabilities depend on the engine's evaluation and the move number, and are computed from a WDL model that can be generated from fishtest data with the help of the scripts in this repository.

Install

Python 3.9 or higher is required.

pip install -r requirements.txt

C++17 compatible compiler is required and zlib needs to be present.

sudo apt-get install zlib1g-dev

Usage

To allow for efficient analysis multiple pgn files are analysed in parallel. Analysis of a single pgn file is not parallelized. Files can either be in .pgn or .pgn.gz format. The script will automatically detect the file format and decompress .pgn.gz files on the fly.

To update Stockfish's internal WDL model, the following steps are needed:

  1. Obtain a large collection of engine-vs-engine games (at fishtest LTC time control) by regularly running python download_fishtest_pgns.py over a period of time. The script will download the necessary pgn files and metadata describing the test conditions from fishtest.

  2. Run the script updateWDL.sh, which will automatically perform these steps:

    • Run make to compile scoreWDLstat.cpp, producing the executable scoreWDLstat.

    • Run scoreWDLstat with some custom parameters to parse the downloaded pgn files. The computed WDL statistics will be stored in a file called updateWDL.json. The file will have entries of the form "('D', 1, 78, 35)": 668132, meaning this tuple for (result, move, material, eval) was seen a total of 668132 times in the processed pgn files.

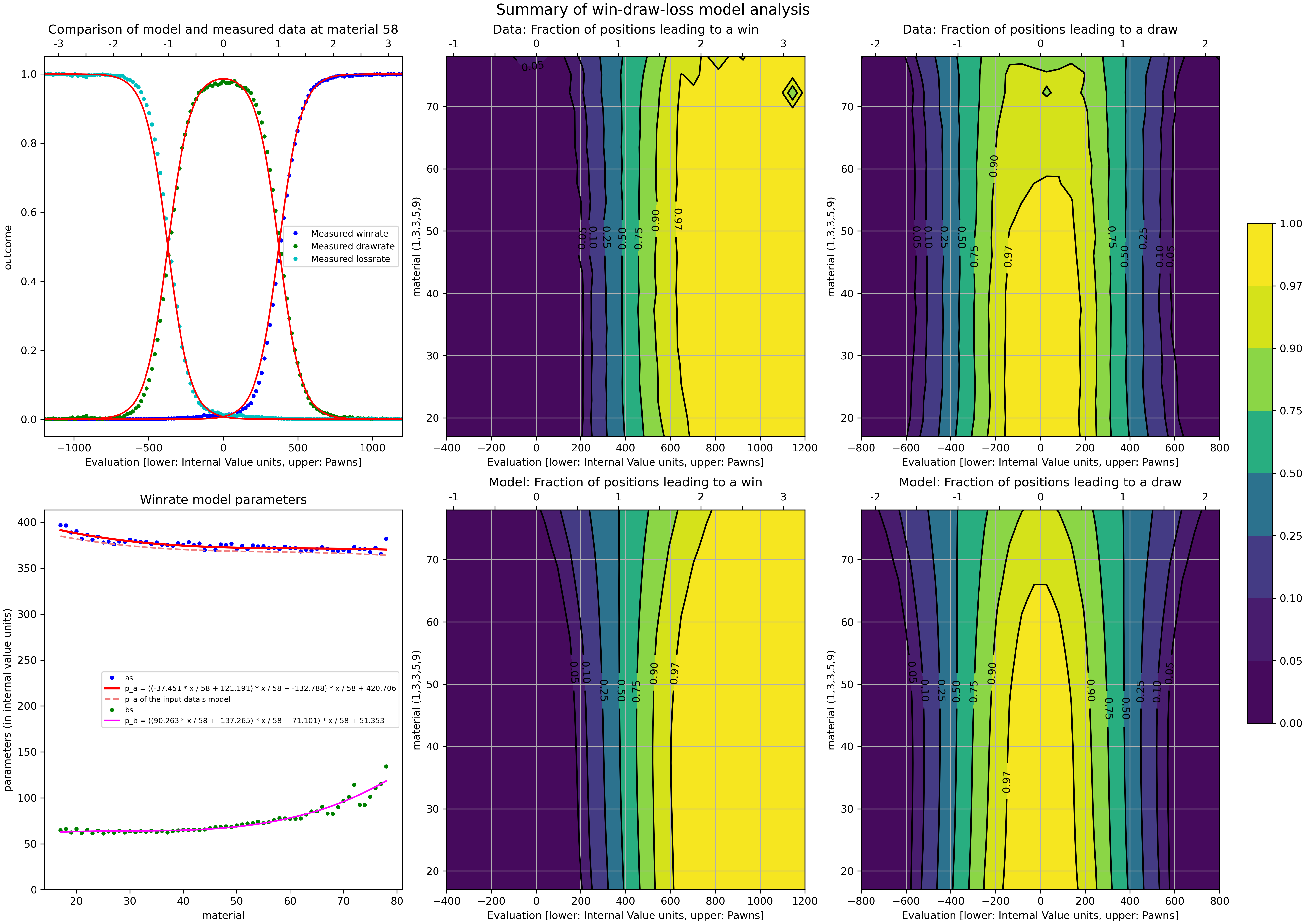
    • Run python scoreWDL.py with some custom parameters to compute the WDL model parameters from the data stored in updateWDL.json. The script's output will be stored in scoreWDL.log and will contain the new values for NormalizeToPawnValue in Stockfish's uci.h and as[], bs[] in uci.cpp. See e.g. official-stockfish/Stockfish#4373. In addition, the script will produce a graphical illustration of the analysed data and the fitted WDL model in the file WDL_model_summary.png, as displayed below.

Results

Help and other options

Running scoreWDLstat --help and python scoreWDL.py --help, respectively, will provide a description of possible command line options for the two programs. For example:

  • scoreWDLstat --matchEngine <regex> : extracts WDL data only from the engine matching the regex
  • python scoreWDL.py --momTarget 30 : chooses move 30 (rather than 32) as target move for the 100cp anchor
  • python scoreWDL.py --momType material --momTarget 68 : bases the fitting on material (rather than move), with 100cp anchor a material count of 68

Background

The underlying assumption of the WDL model is that the win rate for a position can be well modeled as a function of the evaluation of that position. The data shows that a logistic function (see also logistic regression) gives a good approximation of the win rate (the probability of a win) as a function of the evaluation x:

win_rate(x) = 1 / ( 1 + exp(-(x-a)/b))

In this equation, the parameters a and b need to be fitted to the data, which is the purpose of this repository. a is the evaluation for which a 50% win rate is observed, while b indicates how quickly this rate changes with the evaluation. A small b indicates that small changes in the evaluation x quickly turn a game "on the edge" (i.e. a 50% win rate) into a dead draw or a near certain win.

The model furthermore assumes symmetry in evaluation, so that the following quantities follow as well:

loss_rate(x) = win_rate(-x)
draw_rate(x) = 1 - win_rate(x) - loss_rate(x)

This information also allows for estimating the game score

score(x) = 1 * win_rate(x) + 0.5 * draw_rate(x) + 0 * loss_rate(x)

The model is made more accurate by not only taking the evaluation, but also the material or game move counter (mom) into account. (The model currently employed in Stockfish uses the move counter.) This dependency is modeled by making the parameters a and b a function of mom. The win/draw/loss rates are now 2D functions, while a and b are replaced by 1D functions. For example:

win_rate(x,mom) = 1 / ( 1 + exp(-(x-p_a(mom))/p_b(mom)))

Here for simplicity the 1D functions p_a and p_b are chosen to be polynomials of degree 3.

The parameters that need to be fitted to represent the model completely are thus the 8 coefficients that determine these two polynomials. For example:

p_a(mom) = ((-1.719 * mom / 32 + 12.448) * mom / 32 + -12.855) * mom / 32 + 331.883
p_b(mom) = ((-3.001 * mom / 32 + 22.505) * mom / 32 + -51.253) * mom / 32 + 93.209

In order to fit these 8 parameters three different approaches are provided: fitDensity, optimizeProbability, optimizeScore. The simplest one (fitDensity), in a first step, and for each value of mom that is of interest, estimates the best values of a and b to fit the logistic win rate function win_rate(x) to the observed win densities. Note that this procedure, for each value of mom, fits a 1D curve to a horizontal slice of the (x,mom) data. Denoting these obtained values by a(mom) and b(mom), a second step then consists of fitting the 1D polynomials p_a and p_b to these discrete values. The options optimizeProbability and optimizeScore are a bit more sophisticated. They first take, for each value of mom, the discrete values a(mom) and b(mom) provided by the above described simple 1D fitting as initial guesses for an iterative optimization procedure that aims to either maximize the probability of predicting the correct game outcome for the available data, or to minimize the squared error in the predicted score. These improved values of a(mom) and b(mom) then yield newly fitted 1D polynomials p_a and p_b, which in turn form initial values for a final iterative optimization that aims to find the best polynomials p_a and p_b for the objective functions of interest, but now evaluated globally, over the whole 2D data (x,mom).

Interplay with Stockfish

Observe that x in the above formulas is the internal engine evaluation of a position, often also called non-normalized evaluation, which is in general not exposed to the user. By definition x = p_a(mom) is the internal evaluation with a 50% win rate at material or game move counter mom. Ideally this x should be scaled to the displayed evalution 1.0 for every value of mom. But for computational simplicity, in Stockfish all values of x, irrespective of the value of mom, are rescaled to x/p_a(32), which thanks to the choice of p_a is just the sum of the four coefficients of the polynomial p_a, and in rounded form is stored within NormalizeToPawnValue.

In turn, this repository needs the value of NormalizeToPawnValue to recover the internal engine evaluations from the normalized evaluations stored in the pgn files.

Interpretation

The three plots in the graphic displayed above can be interpreted in the following way. The middle and right plot in the first row show contour plots in the (x,mom) domain of the observed win and draw frequencies in the data, respectively. Below them are the corresponding contour plots for the fitted model, i.e. for the 2D functions win_rate(x,mom) and draw_rate(x,mom) based on the found optimal 8 parameters. The top left plot shows a slice of the data at the chosen anchor mom=32, together with plots of win_rate(x), draw_rate(x) and loss_rate(x) for the fitted a=p_a(32) and b=p_b(32). Finally, the bottom left plot shows the collection of all the values of a(mom) and b(mom), together with plots of the two polynomials p_a and p_b.

Code style: black