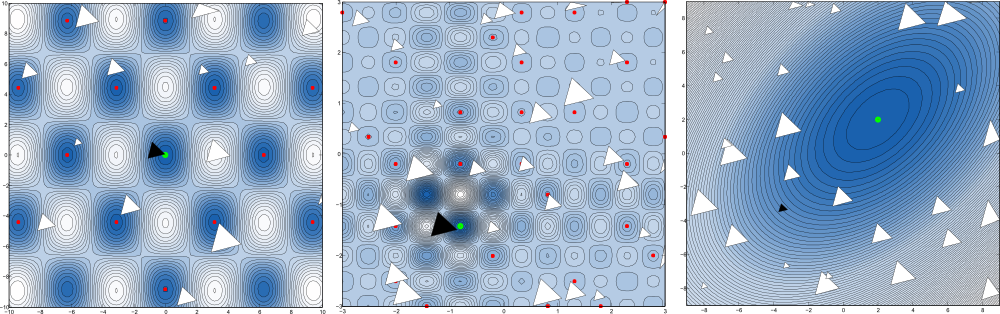
This repository contains the MATLAB/Octave function gbnm that implements the algorithm described in this paper:
Globalized Nelder–Mead method for engineering optimization
by Marco A. Luersen and Rodolphe Le Riche
in Computers & Structures 82.23 (2004) pp.2251-2260.
As the title implies, it is a classical Nelder-Mead method with some extras for dealing with multiple local optima in the objective function.
octave:1> gbnm(@(x) norm(x - [2; 1]), [-5; -5], [5; 5])
ans =
2.00050
0.99941
The Nelder-Mead algorithm, sometimes also called downhill simplex method, was originally published in 1965. It is an iterative algorithm for local, unconstrained minimisation of a non-linear objective function f : R^n --> R. In contrast to most other iterative algorithms, it does not rely on the derivative of the objective function, but only operates on function values directly. This makes it extremely well suited for cases when the target function is not an algebraic term, but a simulation model. It also does not approximate the function's gradient but is based on geometrical projections of a polygon consisting of n+1 points — the simplex — in the n-dimensional parameter space of the objective function. A simplex in two dimensions is a triangle, one in three dimensions is a tetrahedron. In general, the simplex can be represented as a matrix S \in R^{n×n+1} of its points x_i as column vectors:
S = [x_0 ... x_N] with each x_i \in R^n
The basic idea behind the simplex algorithm is that the worst point of S is replaced by a better one with a smaller function value and to repeat this operation iteratively until a local optimum has been found. To achieve this, three different transformations are applied to the simplex which let it move in directions of descent and shrink around a local minimum. These transformations are called reflection, expansion and contraction.
In each iteration, first the worst point is reflected at the centroid of the remaining points. Depending on the quality (good or bad) it then replaces the worst point in the simplex. If the reflected point is not better, it is withdrawn and the other fallback operations are executed.
The globalized Nelder-Mead method just generalizes this idea to find a global minimum. Instead of initialising the simplex once, multiple simplices are initialised and each one finds one local minimum. There are some tweaks to make the location of these simplices better than random, but principally they are spread randomly within a pre-determined search space - an n-dimensional cuboid.
The function itself has the following signature:
[x, fval, output, options] = gbnm(fun,xmin,xmax[, options])
fun A handle of the function to be minimized
xmin Column vector of lower bounds of search space
xmax Column vector of upper bounds of search space
options (optional) Structure with optimization algorithm parameters
x The found global minimum
fval Function value at the found best minimum
output Structure with all found local minima and initial simplices
options Structure of parameters which were used during optimization
options.maxRestarts = 15; % maximum (probablistic or degenerated) restarts
options.maxEvals = 2500; % maximum function evaluations
options.nPoints = 5; % number of random points per restart
options.maxIter=250; % maximum iterations per restart
options.alpha = 1; % reflection coeff
options.beta = 0.5; % contraction coeff
options.gamma = 2; % expansion coeff
options.epsilon = 1e-9; % T2 convergence test coefficient
options.ssigma = 5e-4; % small simplex convergence test coefficient
More details on the options and the can be found in the original paper linked above, or by inspecting this function's source code.
This might become an FAQ section, if any Q's will being asked.
- From my experience, the number of parameters
nshould be small, which means up to 5 or 6.
In other words: this heuristics scales pretty badly with higher number of parameters. - As this heuristics generally needs many (think: hundreds to thousands) evaluations of the objective function, its runtime should be as short as possible (think: fractions of a second).
Copyright (C) 2015, 2016, 2018 Johannes Dorfner
This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/