This repository contains a small, template-based BSpline library in C++ (>= C++17), geared towards the use as basis functions in analytical problems. The main library can be found in the include/ directory. To use the library,
all you have to do is to add this folder to the include path.
BSplines have a number of advantageous properties for the use as basis functions. Some of these advantages are:
- They are very versatile and can be adapted to many different problems.
- The parametrization is very intuitive.
- They have a finite support, ensuring that each spline overlaps only with a few neighbor splines. They can therefore be used in sparse-matrix scenarios.
- Many integrals can easily be evaluated analytically which makes the calculations quite fast and reasonably accurate.
For a case study on the numerical properties of a BSpline basis, see here.
- They are only finitely many times continuously differentiable. Please make sure to also read the Cautions section.
- They are not orthogonal. Using the BSplines as basis functions in eigenvalue problems will usually result in generalized, algebraic eigenvalue problems of the kind
A x = lambda B x(still self-adjoint, though).
The first step to generate a basis set of BSplines is to define the knots vector. From the knots, a set of BSplines can be generated using the bspline::BSplineGenerator or the convenience method bspline::generateBSplines() based on it.
#include <bspline/Core.h>
static constexpr size_t SPLINE_ORDER = 3;
using Spline = bspline::Spline<double, SPLINE_ORDER>;
// Define knots vector.
const std::vector<double> knots{0.0, 1.0, 2.0, 3.0, 4.0, 5.0};
// Generate Splines.
const std::vector<Spline> = bspline::generateBSplines<SPLINE_ORDER>(knots);The corresponding splines are shown in the following graphic. The splines are third order splines and two times continuously differentiable.
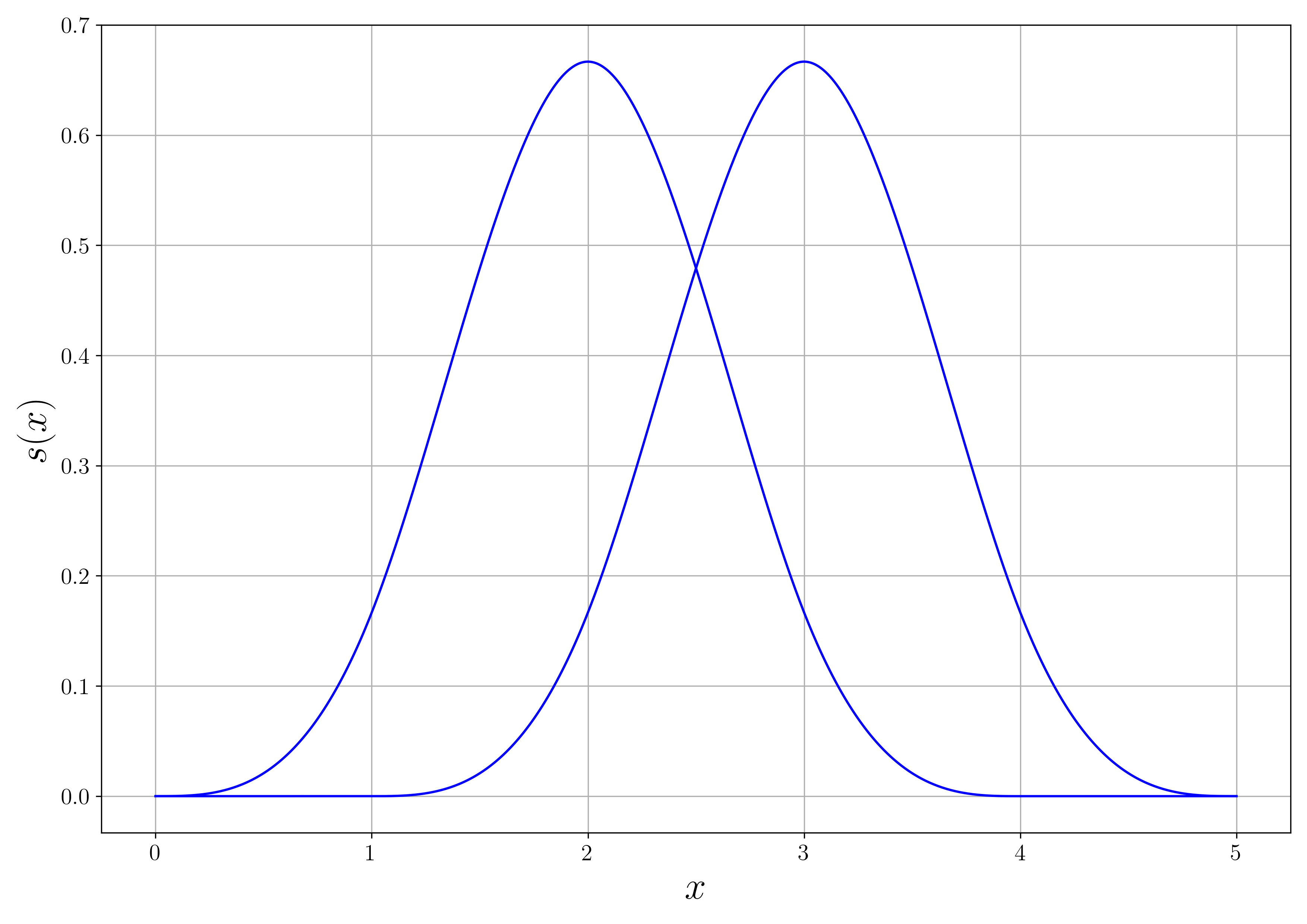
The overall continuity properties of the basis can be controlled by adding certain knots repeatedly. Every additional insert of a knot reduces the continuity at the corresponding grid point by one order. Using, e.g., the knots vector
const std::vector<double> knots{0.0, 0.0, 0.0, 0.0, 1.0, 2.0, 3.0, 4.0, 5.0};the following BSplines are generated:
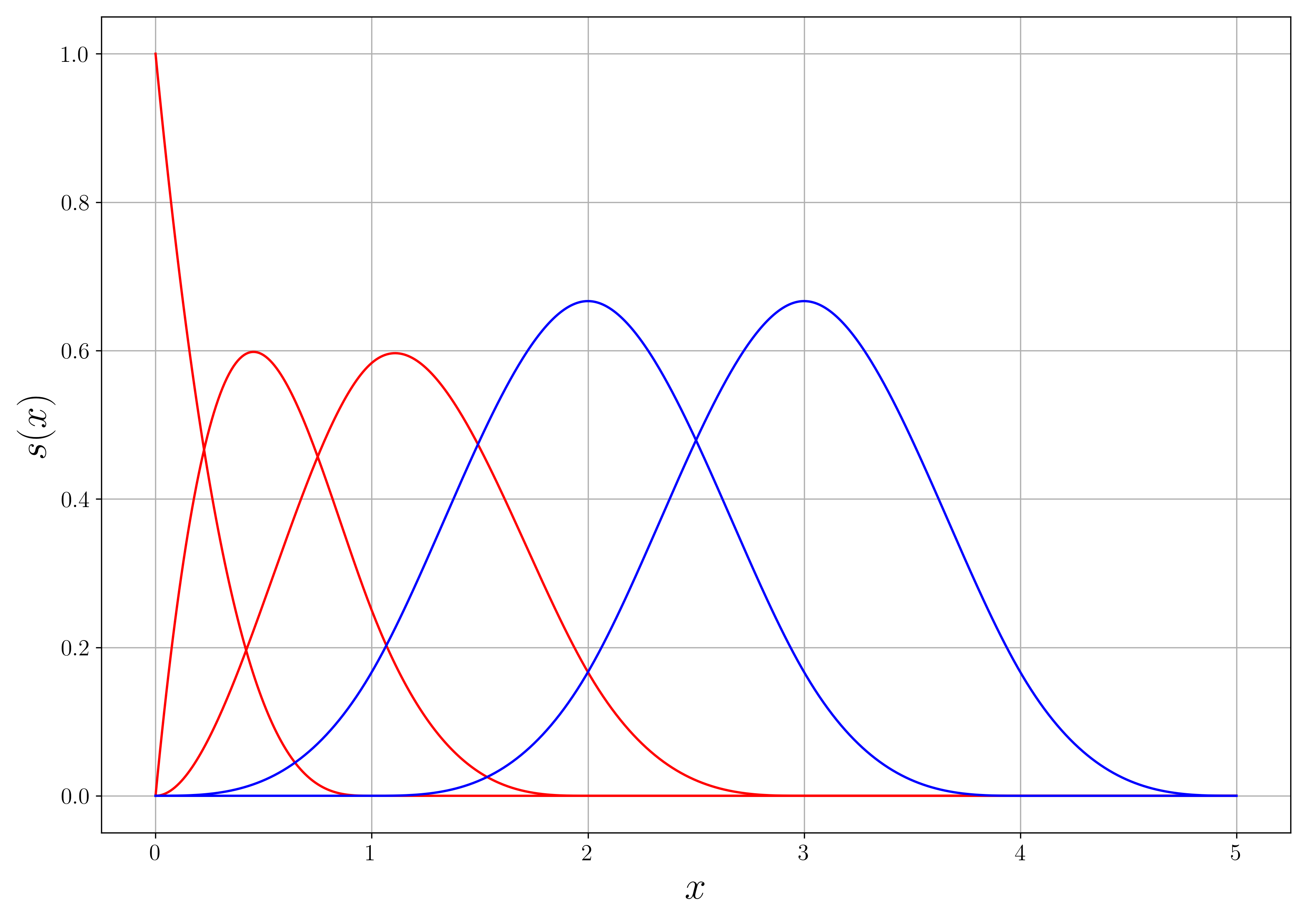
The three red splines were added. They are, respectively, continuous up to the first derivative, the zeroth derivative and not continuous at all at x=0. This approach can be used to bake boundary conditions into the basis. For additional information, the user is referred to the literature on BSplines, e.g. the Wikipedia article.
The library provides a class bspline::integration::BilinearForm for the evaluation of many common matrix elements. To evaluate the matrix element of the Hamiltonian of the harmonic oscillator, you can use
#include <bspline/Core.h>
using namespace bspline::operators;
using namespace bspline::integration;
// [...] Generate spline1 and spline2.
const auto hamiltonOperator = 0.5 * (-Dx<2>{} + X<2>{});
const BilinearForm bilinearForm{hamiltonOperator};
const double matrixElement = bilinearForm.evaluate(spline1, spline2);
// Typedef for BilinearForm(IdentityOperator{});
const ScalarProduct scalarProduct;
const double overlapMatrixElement = scalarProduct.evaluate(spline1, spline2);A full implementation of the solution of the harmonic oscillator and the radial hydrogen problem can be found in the folder examples/.
Note: There is also a bspline::integration::LinearForm.
The core library does not have any additional dependencies beyond a C++ compiler supporting C++17. Everything that is directly or indirectly included by include/bspline/Core.h is considered part of the core library. Parts that are not part of the core library are:
- The contents of
include/bspline/interpolation/.- The interpolation needs a linear algebra framework to solve the linear equation system arising during the interpolation. You can use your linear algebra framework of choice with relative ease, or use interpolation based on
armadillo(only double precision) andEigenprovided by the library. For details, see the source or docs.
- The interpolation needs a linear algebra framework to solve the linear equation system arising during the interpolation. You can use your linear algebra framework of choice with relative ease, or use interpolation based on
- The contents of
include/bspline/integration/numerical.h.- The numerical integration routine implemented there is based on the Gauss-Legendre quadrature scheme provided by
Boost::math.
- The numerical integration routine implemented there is based on the Gauss-Legendre quadrature scheme provided by
Furthermore, the tests and examples require Eigen to compile and the tests are based on Boost::test.
The tests are currently only run regularly on an x64 linux platform using gcc and clang. The main library should be usable with every standard-conformant C++ compiler supporting C++17. If you are using the library on a different platform, I would be happy to receive your feedback.
The operators implemented in include/bspline/operators/ assume that the result of their application to a spline can again be represented as a spline. As each spline is only finitely many times continuously differentiable, this is not true for every application of a derivative operator to a spline. If the spline is not sufficiently many times continuously differentiable, Dirac delta distributions may arise during the application, which are not handled at all by the library. It is left up to the user of the library to make sure that the aforementioned assumption holds true.
The Doxygen docs can be found here.
If you are not familiar with BSplines, a good place to start is the Wikipedia article.