Algoritmo de busca da menor rota entre 20 municípios paulistas
Esse projeto foi desenvolvido para a disciplina de Otimização e Simulação e entregue dia 24/06/2022 durante a minha graduação em Ciência de Dados e Inteligência Artificial na PUC-SP
O Problema do Caixeiro Viajante é um problema que tenta determinar a menor rota para percorrer uma série de cidades (visitando uma única vez cada uma delas), retornando à cidade de origem. Ele é um problema de otimização NP-difícil inspirado na necessidade dos vendedores em realizar entregas em diversos locais (as cidades) percorrendo o menor caminho possível, reduzindo o tempo necessário para a viagem e os possíveis custos com transporte e combustível. (1)
O objetivo deste projeto é desenvolver um algorítmo que encontre a melhor rota entre pelo menos 20 cidades do estado de São Paulo, partindo da capital e retornando a ela no final, sem repetição de cidades (problema do caixeiro viajante). Caso o número de cidades seja inferior a 20, o projeto deve permitir que o usuário especifique quais cidades serão utilizadas no cálculo. Será necessário utilizar um algoritmo de preferência do desenvolvedor e criar um mapa para ilustrar a solução obtida. O objetivo final é apresentar uma solução precisa e visualmente atraente para o problema proposto.
O dataset cidades_sp.tsv foi gerado por mim com base no caderno Mapas2.ipynb disponibilizado pelo professor como material de apoio. Ele apresenta a distância entre municípios do estado de São Paulo para cada um dos municípios
⚠ Importante
- O ponto que representa cada município foi definido como o centro geográfico de cada município
- As distâncias calculadas são as distâncias em linha reta entre os centros geográficos e não a distância real via estrada, por exemplo
Amostra do dataset:
| origem | destino | distancia |
|---|---|---|
| Adamantina | Adamantina | 0.000000 |
| Adamantina | Adolfo | 148.940883 |
| Adamantina | Aguaí | 418.569402 |
| Adamantina | Águas da Prata | 453.052818 |
| Adamantina | Águas de Lindóia | 470.358245 |
Cidades escolhidas para o desafio: Sarapuí, Sarutaiá, Sebastianópolis do Sul, Serra Azul,Serra Negra, Serrana, Sertãozinho, Sete Barras, Severínia,Silveiras, Sorocaba, Sud Mennucci, São Paulo, São Pedro,São Pedro do Turvo, São Roque, São Sebastião,São Sebastião da Grama, São Simão, São Vicente
- Solver: pywrapcp.RoutingModel (2)
- Frameworks usados: OR-Tools, pandas, numpy, geopandas, networkx, folium, matplotlib
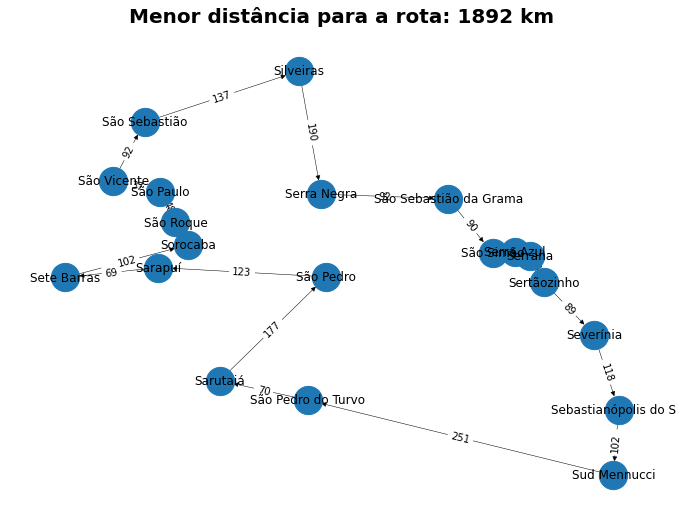
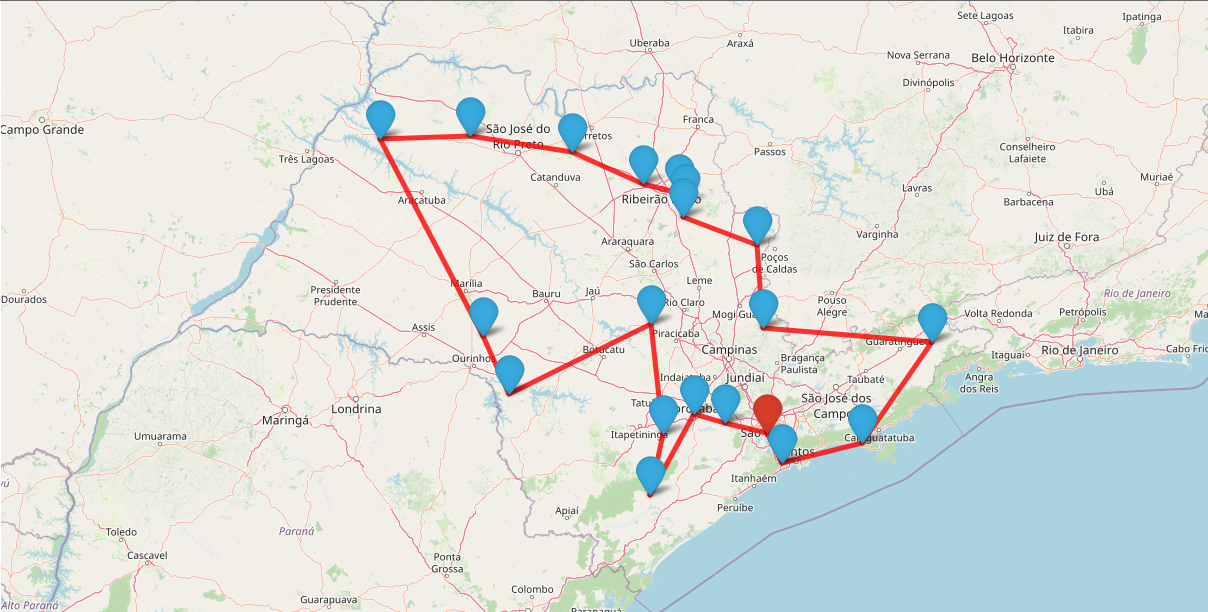
A menor rota que sai da capital paulista e passa por todas as cidades selecionadas e volta para a capital tem 1892 km de extenção
Rota: São Paulo → São Vicente → São Sebastião → Silveiras → Serra Negra → São Sebastião da Grama → São Simão → Serra Azul → Serrana → Sertãozinho → Severínia → Sebastianópolis do Sul → Sud Mennucci → São Pedro do Turvo → Sarutaiá → São Pedro → Sarapuí → Sete Barras → Sorocaba → São Roque → São Paulo
- cada nó (node) representa uma cidade
- os valores dos vértices (edges) representam a distância entre dois nós
- a distribuição espacial não reflete a distribuição geográfica real
- distribuição espacial real dos pontos
- as retas em vermelho representam a distância considerada entre os municípios
- o ponto em vermelho representa o município de São Paulo, que é o ponto de partida e o ponto final de chegada da rota
- os pontos em azul representam os demais municípios
Uma vez que desenvolvi um método para calcular as distâncias entre uma amostra das cidades do estado, uma oportunidade futura é calcular cenários sem restrições de quantidade de cidades, por exemplo:
- qual é a rota mais curta que passa por TODAS as cidades do estado de São Paulo?
- qual é a rota mais longa que passa por TODAS as cidades do estado de São Paulo?
- qual é a rota mais curta que passa por TODAS as cidades do Brasil?
- qual é a rota mais longa que passa por TODAS as cidades do Brasil?
Contudo, tais implementações irão precisar de um poder computacional muito maior para resolver o problema na mesma escala de tempo que a solução desse projeto. Para uma solução em força-bruta, a escala de complexidade desse problema é
Por fim, ao invés de considerar a distância em linha reta entre os municípios, podemos calcular a distância entre eles pela estrada e isso resultaria em um resultado mais preciso.
(1) Problema do caixeiro-viajante. In: WIKIPÉDIA: a enciclopédia livre. Disponível em: https://pt.wikipedia.org/wiki/Problema_do_caixeiro-viajante. Acesso em: 24 fev. 2023.
(2) Traveling Salesperson Problem. In: OR-Tools: fast and portable software for combinatorial optimization. Disponível em: https://developers.google.com/optimization/routing/tsp. Acesso em: 24 fev. 2023.