This package is for finding change points in sequences of responses. Putative change points are first detected, then a statistical test at a predefined significance level (Criterion) is applied to decide if the change point is supported or not. Based on algorithm published by Gallistel et al. (2004), translated from Matlab into R.
You can use devtools to install the package from Github. Install the devtools package first, then execute this code in R(Studio):
devtools::install_github('ontogenerator/cpdetectoR')There is a main wrapper function, called cp_wrapper, which can be used to analyze sequences of responses. The first argument of the function is the input. Thes second argument indicates whether the input contains discrete-trial data (TRUE), or successive real value intervals (FALSE). The third argument gives the statistical test ("KS", "ttest", "binomial", or "chisquare"). The different tests usually give similar, but often different results. The third and last argument is the criterion, with values between 1.3 and 6.
The input can be either a vector:
library(cpdetectoR) # load package first
set.seed(25)
cp_wrapper(c(rbinom(50, 1, 0.3), rbinom(50, 1, 0.8)), TRUE, "binomial", 2)
#> Trial CumSs Slopes
#> 1 0 0 0.2173913
#> 2 46 10 0.8518519
#> 3 100 56 0.8518519or a data frame:
d_responses <- data.frame(Responses = c(rbinom(50, 1, 0.3), rbinom(50, 1, 0.8)))
cp_wrapper(d_responses, TRUE, "chisquare", 2)
#> Trial CumSs Slopes
#> 1 0 0 0.08
#> 2 25 2 0.36
#> 3 50 11 0.82
#> 4 100 52 0.82For the same value of the criterion, the chi square test usually gives a higher number of change points (in this case, false positives) than the binomial test. The value of the criterion should lie between 1.3 and 6, corresponding to p values of 0.05 and 0.000001, respectively. These values are the logarithms of the odds against the null (no-change) hypothesis.
Let us look first at the included eyeblink data set:
eyeblink[,] # inspect data set
#> [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [36] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1
#> [71] 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 0 0
#> [106] 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1
#> [141] 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1
#> [176] 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1
#> [211] 0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1
#> [246] 1 0 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 0 1 1 0
#> [281] 1 1 1 0 1 0 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 0 1
#> [316] 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1
#> [351] 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1
#> [386] 1 1 0 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 0
#> [421] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [456] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [491] 0 0 0 0 0 0 0 0 0 0Gallistel et al. advise against using the chi square test on these data. Indeed, with a criterion of 2, the test fails:
cp_wrapper(eyeblink, TRUE, "chisquare", 2)However, using either a higher criterion or the "binomial" test gives a result:
cp_wrapper(eyeblink, TRUE, "chisquare", 3)
#> Trial CumSs Slopes
#> 1 0 0 0.0000000
#> 2 65 0 0.6528736
#> 3 500 284 0.6528736
cp_wrapper(eyeblink, TRUE, "binomial", 2)
#> Trial CumSs Slopes
#> 1 0 0 0.0000000
#> 2 65 0 0.8711340
#> 3 259 169 0.7236842
#> 4 411 279 0.6250000
#> 5 419 284 0.0000000
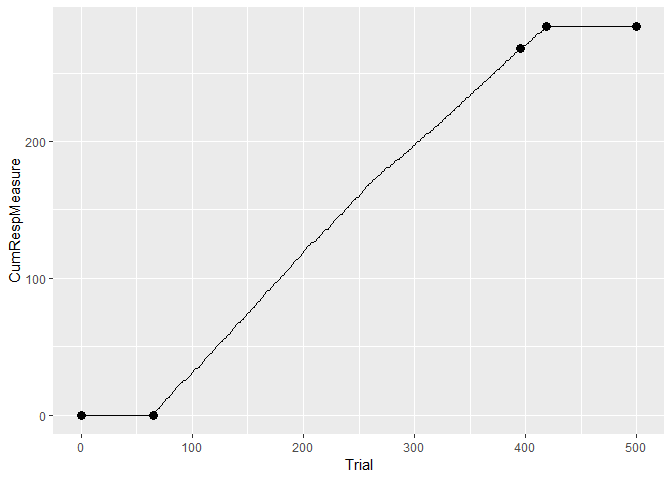
#> 6 500 284 0.0000000With ggplot we can visualize the results by first generating a data.frame with the cumulative responses:
library(ggplot2) # load the ggplot package
eyeblinkdata <- data.frame(Trial = 1:length(eyeblink[,]),
CumRespMeasure = cumsum(eyeblink)[,])
changepoints <- cp_wrapper(eyeblink, TRUE, "binomial", 4) # save the output of the change point analysis
#generate a cumulative response vs trial plot:
ggplot(eyeblinkdata) + geom_line(aes(Trial, CumRespMeasure)) +
geom_point(data = changepoints, aes(Trial, CumSs), size = 3)Another type of plot one can look at is the average response rate per trial vs trial. The plusmaze data set included with the package contains frequency data, that are again preferrably analyzed with the random rate (binomial) test.
plusmaze[,] # inspect data set
#> [1] 0 1 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [36] 0 1 1 1 0 1 0 1 1 1 0 0 1 0 1 0 0 0 0 0 1 0 0 1 1 1 0 1 0 1 0 1 0 1 1
#> [71] 1 0 1 1 1 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 1 1 1 0 1 0 1 1 0 1 1 1
#> [106] 0 1 1 0 1 0 1 1 1 1 0 0 1 1 1 0 1 0 1 0 1 0 1 1 1 1 1 1 0 0 1 1 1 1 0
#> [141] 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 1 0 1 0 0
#> [176] 0 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1 1 0 1 1 0 1 1 1 1
(cp.1 <- cp_wrapper(plusmaze, TRUE, "binomial", 1.3)) #find the change points
#> Trial CumSs Slopes
#> 1 0 0 0.4090909
#> 2 22 9 0.0000000
#> 3 36 9 0.6341463
#> 4 200 113 0.6341463
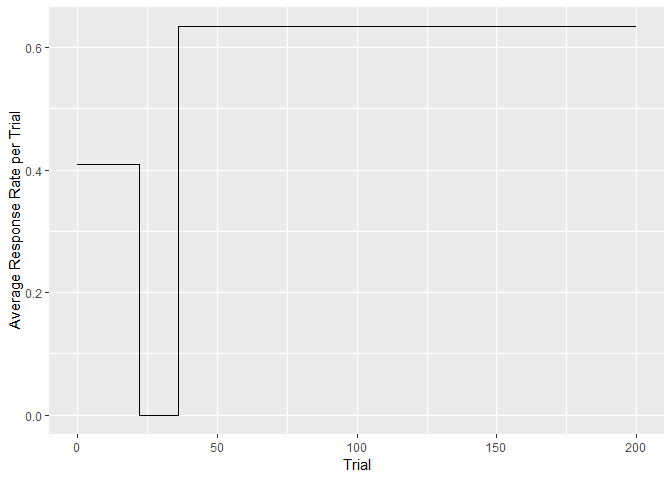
# plot average response rate per trial
ggplot() + geom_step(data = cp.1, aes(Trial,Slopes)) +
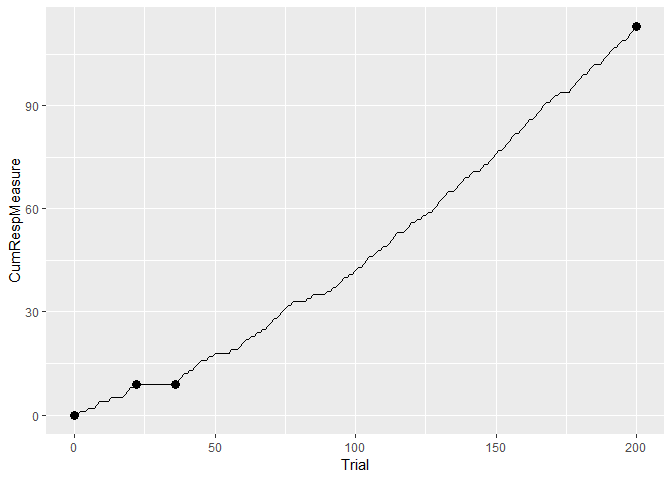
ylab("Average Response Rate per Trial")# for comparison, the cumulative response vs trial plot, as in the example above:
plusmazedata <- data.frame(Trial = 1:length(plusmaze[,]),
CumRespMeasure = cumsum(plusmaze)[,])
ggplot(plusmazedata) + geom_line(aes(Trial, CumRespMeasure)) +
geom_point(data = cp.1, aes(Trial, CumSs), size = 3)The attached data set hopperentry contains hopper-entry speeds from pigeons, an example of normally distributed data. Consequently the t test can be used.
(cp.2 <- cp_wrapper(hopperentry, TRUE, "ttest", 4)) #find the change points
#> Trial CumSs Slopes
#> 1 0 0.00000 0.7132600
#> 2 42 29.95692 0.8891728
#> 3 100 81.52894 0.9880297
#> 4 244 223.80522 0.9880297
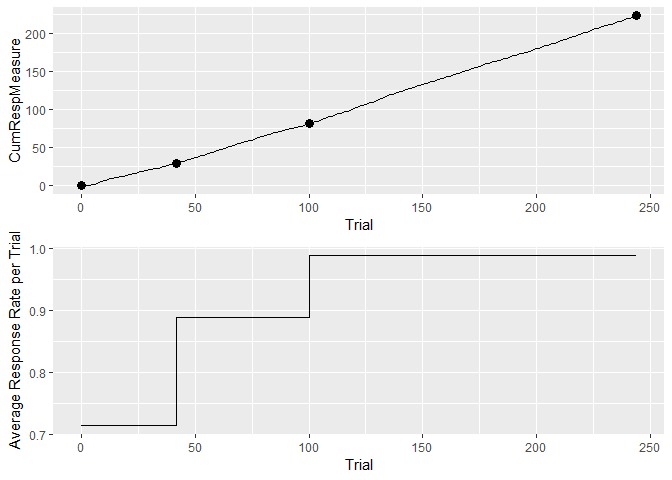
# cumulative response vs trial plot
hedata <- data.frame(Trial = 1:length(hopperentry[,]),
CumRespMeasure = cumsum(hopperentry)[,])
pl1 <- ggplotGrob(ggplot(hedata) + geom_line(aes(Trial, CumRespMeasure)) +
geom_point(data = cp.2, aes(Trial, CumSs), size = 3))
# plot average response rate per trial
pl2 <- ggplotGrob(ggplot(cp.2) + geom_step(aes(Trial, Slopes)) +
ylab("Average Response Rate per Trial"))
# stack the two plots vertically using the grid package
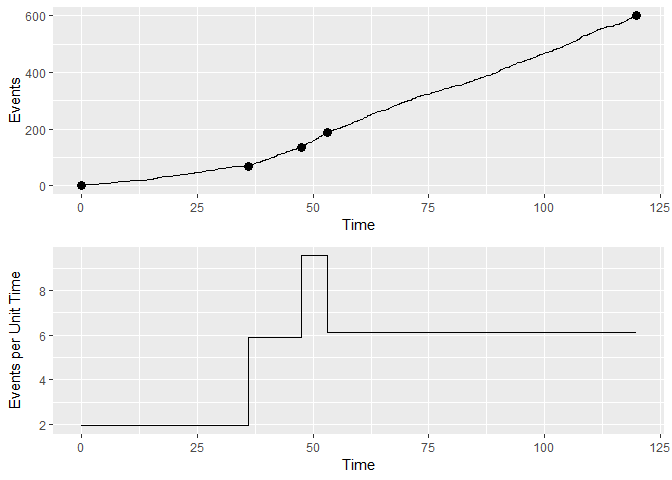
grid::grid.draw(rbind(pl1, pl2, size = "first"))An example for continuous data is the attached matching data set. The plots need different axes and labels:
(cp.3 <- cp_wrapper(matching, FALSE, "binomial", 2)) #find the change points
#> Time Events Slopes
#> 1 0.00000 0 1.934973
#> 2 36.17621 70 5.898969
#> 3 47.53413 137 9.559500
#> 4 53.07835 190 6.138859
#> 5 119.86601 600 6.138859
# cumulative response vs trial plot
matchingdata <- data.frame(Events = 1:length(matching[,]),
Time = cumsum(matching)[,])
pl3 <- ggplotGrob(ggplot(matchingdata) + geom_line(aes(Time, Events)) +
geom_point(data = cp.3, aes(Time, Events), size = 3))
# plot average response rate per trial
pl4 <- ggplotGrob(ggplot(cp.3) + geom_step(aes(Time, Slopes)) +
ylab("Events per Unit Time"))
grid::grid.draw(rbind(pl3, pl4, size = "first"))- Gallistel CR, Fairhurst S, Balsam P (2004) The learning curve: Implications of a quantitative analysis. PNAS 101:13124-13131. doi: 10.1073/pnas.0404965101