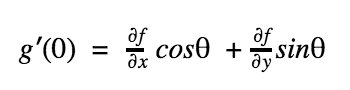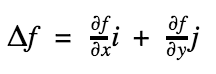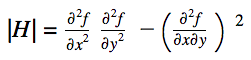Adından da anlaşılacağı gibi, gradyen yöntemleri, optimumu belirleyen etkili algoritmalar üretmek için türev bilgilerini doğrudan kullanır. En hızlı artan veya en hızlı azalan yön olarak da adlandırılır. İlk adım olarak bir başlangıç noktası seçilir ve amaç fonksiyonunu en hızlı geliştiren yönde hareket edilir.
Bir boyutlu fonksiyonun birinci türevi, diferansiyeli alınan fonksiyonun eğilimini veya o noktadaki teğetini ifade eder.
Örneğin; eğimin pozitif olması, bağımsız değişkeni artırmanın incelenen fonksiyonun değerini artıracağı anlamındadır.
Ayrıca birinci türev fonksiyonun optimum bir noktasına ne zaman erişeceğini de ifade eder, türevin sıfıra gittiği nokta.
Gradyen
İki boyutlu bir f(x,y) fonksiyonunu ele alalım ve bu fonksiyonun bir dağın üzerindeki konumumuzu temsil ettiğini varsayalım. Dağın üzerinde belirli bir (a,b) konumunda olduğunuzu düşünelim. Herhangi bir doğrultudaki eğim; yönü belirtmenin bir yolu, yöne bağlı gradyen x ekseni ile θ açısı yapan bir h ekseni boyunca tanımlanır. Bu yeni eksen boyunca yükseklik yeni bir g(h) fonksiyonu olarak düşünülebilir. Eğer konumunuzu bu eksenin başlangıcı olarak tanımlarsanız (yani h=0), bu yöndeki eğim g'(0) olacaktır. Yöne bağlı türev adı verilen bu eğim x ve y eksenleri boyunca alınan kısmi türevlerle hesaplanabilir.
Burada kısmi türevler x=a ve y=b noktalarında hesaplanmıştır. Amacımız, bir sonraki adımda en fazla yükseltiyi sağlamak olduğundan; "En dik çıkış hangi yöndedir ?" sorusuna yanıt bulmamız gerekir.
Gradyen (Del f olarak da adlandırılan vektör) yukarıdaki şekildeki gibi ifade edilir. f(x,y) fonksiyonunun x=a ve y=b noktasındaki yöne bağlı türevini ifade eder.
Gradyeni nasıl kullanırız?
Dağa tırmanma problemi için, eğer en hızlı şekilde yükseklik kazanmak istiyorsak gradyen bize yerel olarak hangi yönde ilerlememiz gerektiğini ve bu yönde gidersek ne kadar kazanacağımızı söyler. Ancak bu stratejinin bizi her zaman doğrudan zirveye ulaştırmayacağını unutmamalıyız.
Hessian
Bir boyutlu problemlerde hem birinci türev hem de ikinci türev optimumun aranmasında önemlidir. Birinci türev (i ) fonksiyonun en dik yörüngesini belirler ve (ii ) optimuma ulaşıldığını belirtir. Optimum noktasına gelindiğinde ikinci türev bir maksimumda mı (negatig f''(x)) yoksa bir minimumda mı (pozitif f''(x)) olduğumuzu söyler. Bir minimum mu yoksa maksimum mu olduğunu sadece x ve y’ye göre ikinci türevlerle değil aynı zamanda x ve y’ye göre karışık ikinci türeve de bağlıdır.
Üç durum söz konusu olabilir:
Çok boyutlu bir fonksiyonun optimuma ulaşıp ulaşmadığını anlamak için bir yol sunmasının yanında Hessian’ın optimizasyonda başka kullanım alanları da vardır.
Örnek 1
(4,2) noktasında basınç gradyeni yönünde bir boyutlu bir denklem geliştirin.Basınç fonksiyonu f(x,y)=5*x2*y-8*y2-7*x*2 şeklinde verilmiştir.
*NOT:PYTHON DİLİYLE YAZILMIŞTIR. VERSİON:2.7
from sympy import *
import math
x=Symbol('x')
y=Symbol('y')
xi=4 #x degeri
yi=2 #y degeri
denklem=5*x**2*y-8*y**2-7*x**2
print "Denklem:"+denklem.diff(x).subs(x,xi).subs(y,yi).__str__()+"cos T + " +denklem.diff(y).subs(x,xi).subs(y,yi).__str__() +"sin T"
ÇIKTI
Denklem:24cos T + 48sin T
Örnek 2
(1,1) noktasında sıcaklık gradyeni yönünde bir boyutlu denklem geliştiriniz.Bir sıcaklık fonksiyonu f(x,y)=2*x3*y2-6*x*y+x*2+4*y şeklinde verilmiştir.
*NOT:PYTHON DİLİYLE YAZILMIŞTIR. VERSİON:2.7
from sympy import *
import math
x = Symbol('x')
y = Symbol('y')
xi = 1 # x degeri
yi = 1 # y degeri
denklem = 2 * x ** 3 * y ** 2 - 6 * x * y + x ** 2 + 4 * y
print "Denklem:" + denklem.diff(x).subs(x, xi).subs(y, yi).__str__() + "cos T + " + denklem.diff(y).subs(x, xi).subs(y,yi).__str__() + "sin T"
ÇIKTI
Denklem:2cos T + 2sin T