State-of-the-art bilingual open-sourced Math reasoning LLMs. A solver, prover, verifier, augmentor.
- [2024.01.31] We add MiniF2F results with evaluation codes!
- [2024.01.29] We add checkpoints from ModelScope. Update results about majority voting and Code Intepreter. Tech report is on the way!
- [2024.01.26] We add checkpoints from OpenXLab, which ease Chinese users to download!
- 7B and 20B Chinese and English Math LMs with better than ChatGPT performances. InternLM2-Math are continued pretrained from InternLM2-Base with ~100B high quality math-related tokens and SFT with ~2M bilingual math supervised data. We apply minhash and exact number match to decontaminate possible test set leakage.
- Add Lean as a support language for math problem solving and math theorem proving. We are exploring combining Lean 3 with InternLM-Math for verifiable math reasoning. InternLM-Math can generate Lean codes for simple math reasoning tasks like GSM8K or provide possible proof tactics based on Lean states.
- Also can be viewed as a reward model, which supports the Outcome/Process/Lean Reward Model. We supervise InternLM2-Math with various types of reward modeling data, to make InternLM2-Math can also verify chain-of-thought processes. We also add the ability to convert a chain-of-thought process into Lean 3 code.
- A Math LM Augment Helper and Code Interpreter. InternLM2-Math can help augment math reasoning problems and solve them using the code interpreter which makes you generate synthesis data quicker!
InternLM2-Math-Base-7B and InternLM2-Math-Base-20B are pretrained checkpoints. InternLM2-Math-7B and InternLM2-Math-20B are SFT checkpoints.
| Model | Model Type | Transformers(HF) | OpenXLab | ModelScope | Release Date |
|---|---|---|---|---|---|
| InternLM2-Math-Base-7B | Base | 🤗internlm/internlm2-math-base-7b |  |
 internlm2-math-base-7b internlm2-math-base-7b |
2024-01-23 |
| InternLM2-Math-Base-20B | Base | 🤗internlm/internlm2-math-base-20b |  |
 internlm2-math-base-20b internlm2-math-base-20b |
2024-01-23 |
| InternLM2-Math-7B | Chat | 🤗internlm/internlm2-math-7b |  |
 internlm2-math-7b internlm2-math-7b |
2024-01-23 |
| InternLM2-Math-20B | Chat | 🤗internlm/internlm2-math-20b |  |
 internlm2-math-20b internlm2-math-20b |
2024-01-23 |
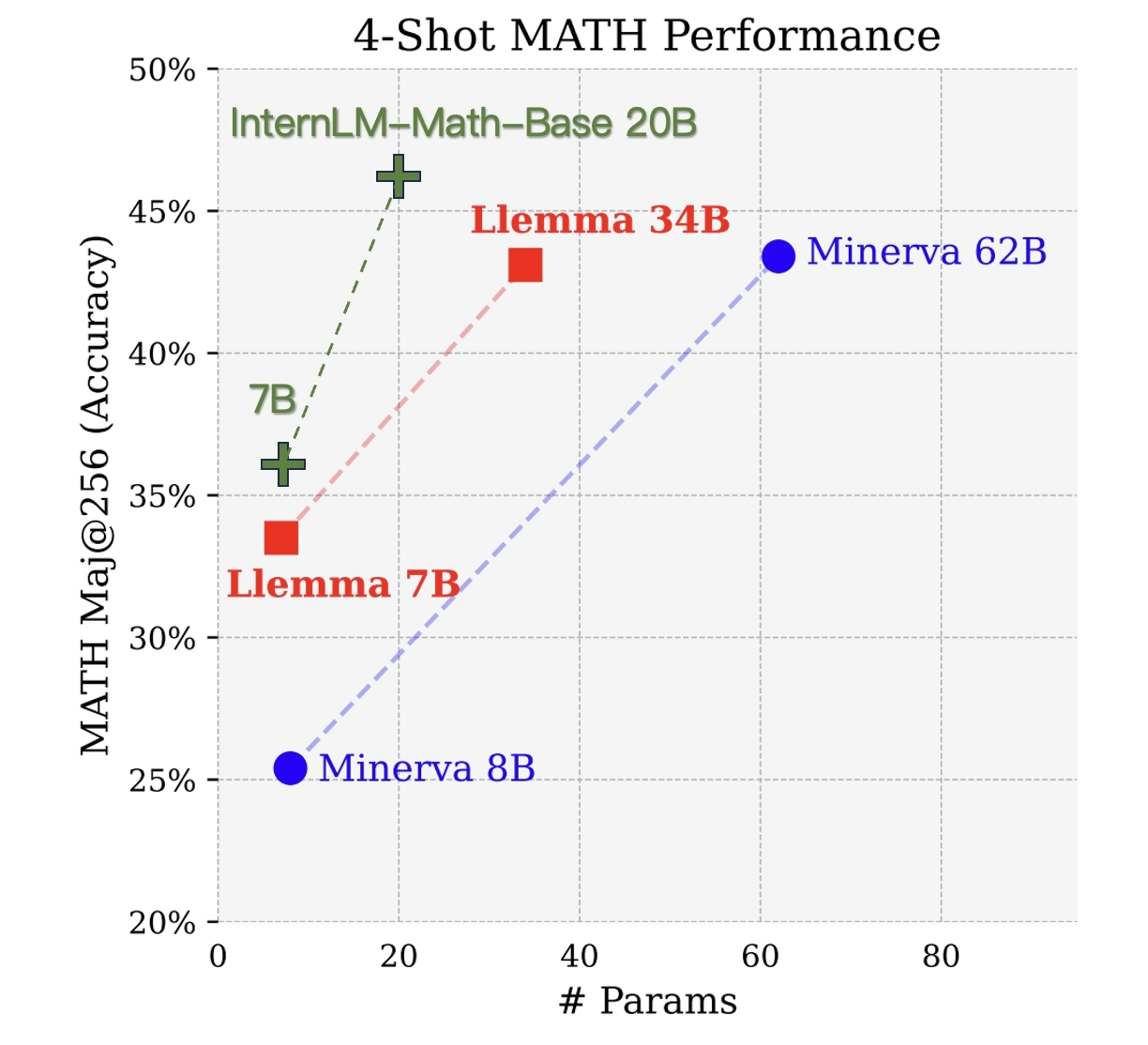
We evaluate pretrain checkpoints based on greedy decoding with few-shot COT. Details of pretraining will be introduced in the tech report.
| Benchmark | GSM8K MAJ@1 | GSM8K MAJ@100 | MATH MAJ@1 | MATH MAJ@256 |
|---|---|---|---|---|
| Llama2-7B | 14.6 | - | 2.5 | - |
| Llemma-7B | 36.4 | 54.0 | 18.0 | 33.5 |
| InternLM2-Base-7B | 36.5 | - | 8.6 | - |
| InternLM2-Math-Base-7B | 49.2 | 75.7 | 21.5 | 35.6 |
| Minerva-8B | 16.2 | 28.4 | 14.1 | 25.4 |
| InternLM2-Base-20B | 54.6 | - | 13.7 | - |
| InternLM2-Math-Base-20B | 63.7 | 84.8 | 27.3 | 46.2 |
| Llemma-34B | 51.5 | 69.3 | 25.0 | 43.1 |
| Minerva-62B | 52.4 | 68.5 | 27.6 | 43.4 |
| Minerva-540B | 58.8 | 78.5 | 33.6 | 50.3 |
We evaluate pretrain checkpoints using few-shot on MiniF2F. Please see eval/pretrain/minif2f for evaluation.
| Benchmark | MiniF2F-test |
|---|---|
| ReProver | 26.5 |
| LLMStep | 27.9 |
| Code-Llama-7B | 26.2 |
| Code-Llama-34B | 25.8 |
| Llemma-7B | 26.2 |
| Llemma-34B | 25.8 |
| InternLM2-Math-7B-Base | 30.3 |
| InternLM2-Math-20B-Base | 29.5 |
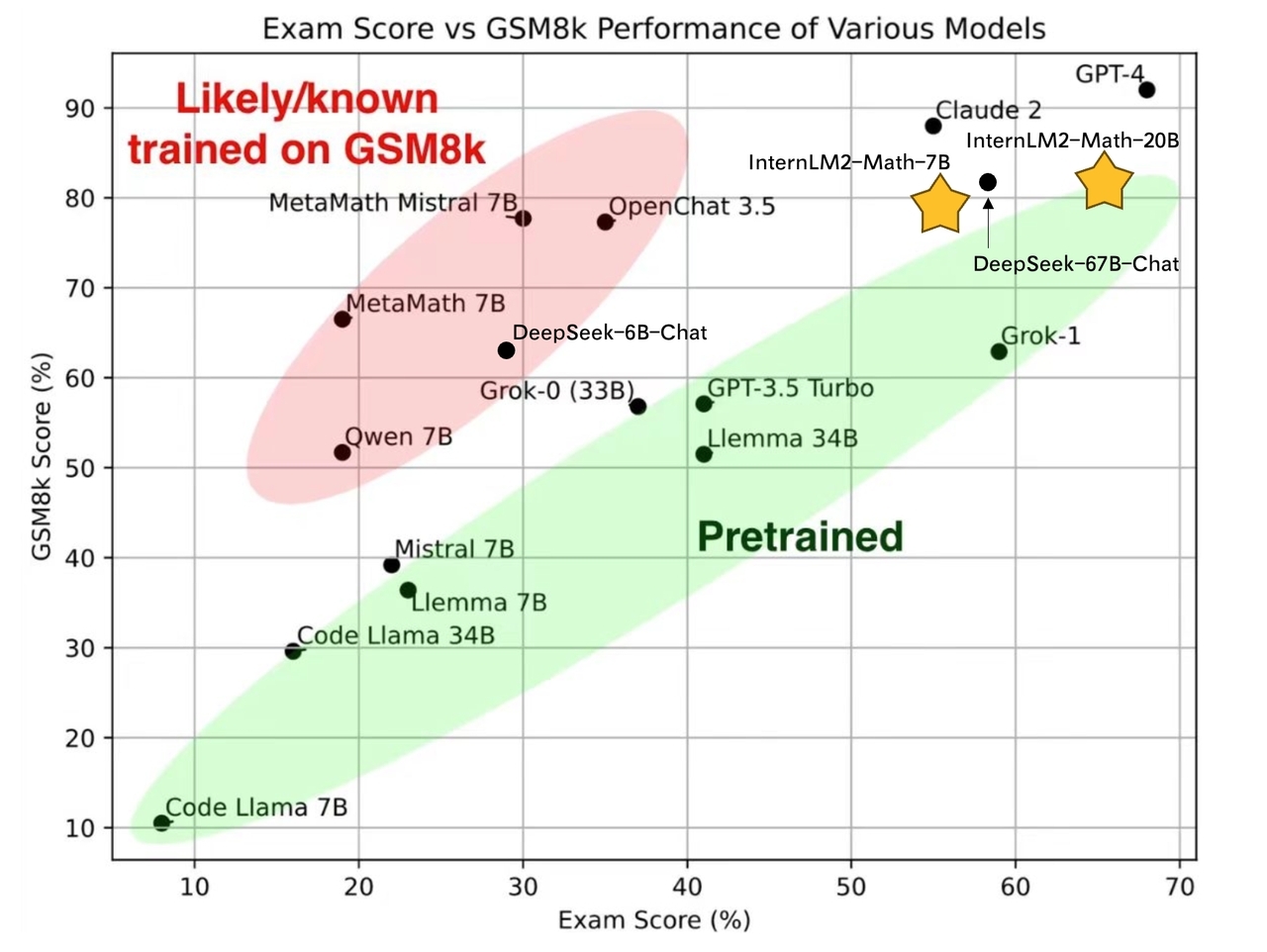
All performance is based on greedy decoding with COT. We notice that the performance of Hungary has a big variance between our different checkpoints, while other performance is very stable. This may be due to the problem amount about Hungary.
| Model | Model Type | GSM8K | MATH | Hungary |
|---|---|---|---|---|
| Qwen-7B-Chat | Genearl | 51.7 | 11.6 | - |
| DeepSeek-7B-Chat | General | 63.0 | 15.8 | 28.5 |
| InternLM2-Chat-7B | General | 70.7 | 23.0 | - |
| ChatGLM3-6B | General | 53.8 | 20.4 | 32 |
| MetaMath-Mistral-7B | Mathematics | 77.7 | 28.2 | 29 |
| MetaMath-Llemma-7B | Mathematics | 69.2 | 30.0 | - |
| InternLM2-Math-7B | Mathematics | 78.1 | 34.6 | 55 |
| InternLM2-Chat-20B | General | 79.6 | 31.9 | - |
| MetaMath-Llemma-34B | Mathematics | 75.8 | 34.8 | - |
| InternLM2-Math-20B | Mathematics | 82.6 | 37.7 | 66 |
| Qwen-72B | General | 78.9 | 35.2 | 52 |
| DeepSeek-67B | General | 84.1 | 32.6 | 58 |
| ChatGPT (GPT-3.5) | General | 80.8 | 34.1 | 41 |
| GPT4 (First version) | General | 92.0 | 42.5 | 68 |
All performance is based on interacting with Python.
| Model | GSM8K | MATH |
|---|---|---|
| DeepSeek-Coder-Instruct-7B | 62.8 | 28.6 |
| DeepSeek-Coder-Instruct-1.5-7B | 72.6 | 34.1 |
| ToRA-7B | 72.6 | 44.6 |
| MathCODER-CL-7B | 67.8 | 30.2 |
| InternLM2-Chat-7B | 77.9 | 45.1 |
| InternLM2-Math-7B | 79.4 | 50.9 |
| ToRA-13B | 75.8 | 48.1 |
| MathCODER-CL-13B | 74.1 | 35.9 |
| InternLM2-Chat-20B | 84.5 | 51.2 |
| InternLM2-Math-20B | 80.7 | 54.3 |
| MathCODER-CL-34B | 81.7 | 45.2 |
| ToRA-70B | 84.3 | 49.7 |
| GPT-4 Code Interpreter * | 97.0 | 69.7 |
You can effortlessly evaluate InternLM2-Math across a diverse array of mathematical datasets, such as Math and GSM8K, using OpenCompass with a single command. To get started, simply execute the following in your terminal after installing OpenCompass:
python run.py --models hf_internlm2_chat_math_7b --datasets gsm8k_gen math_gen_736506Alternatively, for a streamlined experience, you can utilize a predefined configuration file. To do this, run the command below, making sure to adjust the arguments according to your requirements:
python run.py config/eval_internlm_math_chat.pyWe suggest using LMDeploy(>=0.2.1) for inference.
from lmdeploy import pipeline, TurbomindEngineConfig, ChatTemplateConfig
backend_config = TurbomindEngineConfig(model_name='internlm2-chat-7b', tp=1, cache_max_entry_count=0.3)
chat_template = ChatTemplateConfig(model_name='internlm2-chat-7b', system='', eosys='', meta_instruction='')
pipe = pipeline(model_path='internlm/internlm2-math-7b', chat_template_config=chat_template, backend_config=backend_config)
problem = '1+1='
result = pipe([problem], request_output_len=1024, top_k=1)import torch
from transformers import AutoTokenizer, AutoModelForCausalLM
tokenizer = AutoTokenizer.from_pretrained("internlm/internlm2-math-7b", trust_remote_code=True)
# Set `torch_dtype=torch.float16` to load model in float16, otherwise it will be loaded as float32 and might cause OOM Error.
model = AutoModelForCausalLM.from_pretrained("internlm/internlm2-math-7b", trust_remote_code=True, torch_dtype=torch.float16).cuda()
model = model.eval()
response, history = model.chat(tokenizer, "1+1=", history=[], meta_instruction="")
print(response)We list some instructions used in our SFT. You can use them to help you. You can use the other ways to prompt the model, but the following are recommended. InternLM2-Math may combine the following abilities but it is not guaranteed.
Translate proof problem to Lean:
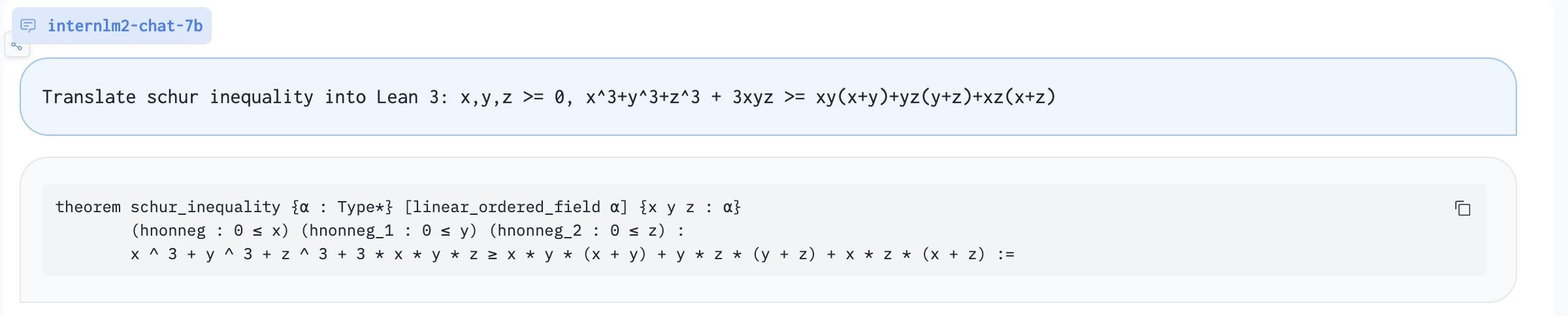
Using Lean 3 to solve GSM8K problem:
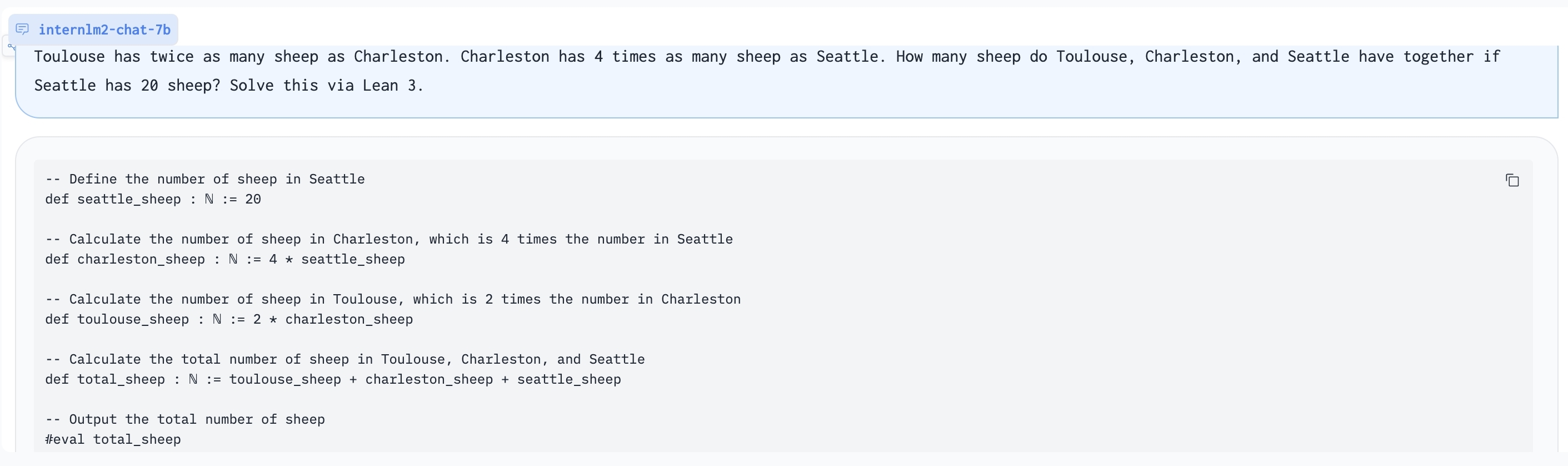
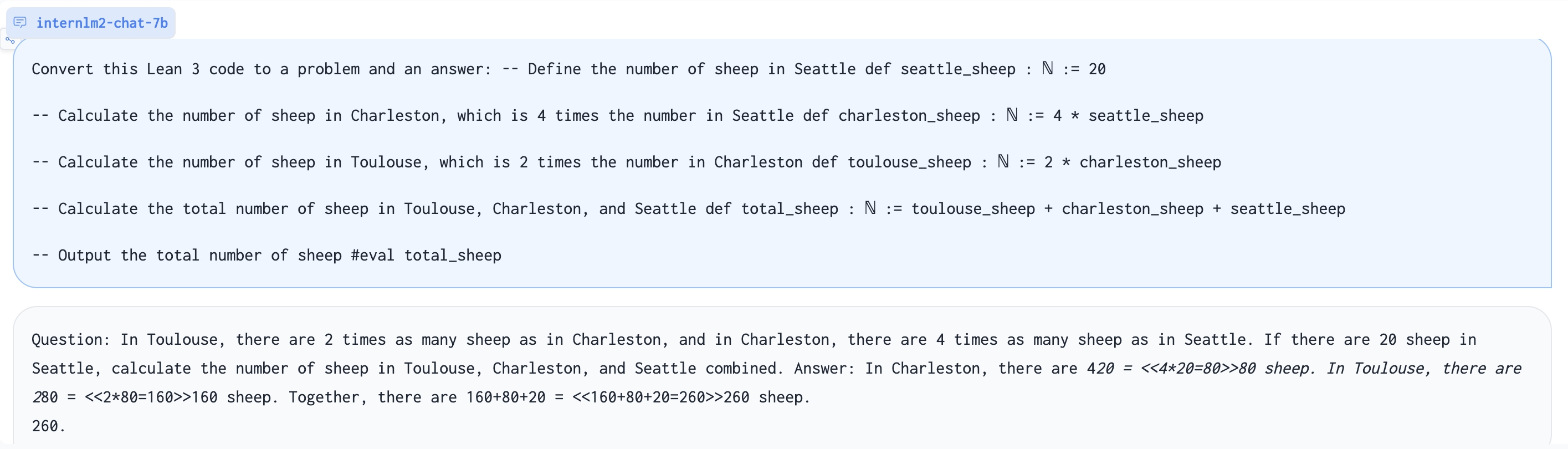
Generate problem based on Lean 3 code:
Augment a harder math problem:

| Description | Query |
|---|---|
| Solving question via chain-of-thought | {Question} |
| Solving question via Lean 3 | {Question}\nSolve this via Lean 3 |
| Outcome reward model | Given a question and an answer, check is it correct?\nQuestion:{Question}\nAnswer:{COT} |
| Process reward model | Given a question and an answer, check correctness of each step.\nQuestion:{Question}\nAnswer:{COT} |
| Reward model | Given a question and two answers, which one is better? \nQuestion:{Question}\nAnswer 1:{COT}\nAnswer 2:{COT} |
| Convert chain-of-thought to Lean 3 | Convert this answer into Lean3. Question:{Question}\nAnswer:{COT} |
| Convert Lean 3 to chain-of-thought | Convert this lean 3 code into a natural language problem with answers:\n{LEAN Code} |
| Translate question and chain-of-thought answer to a proof statement | Convert this question and answer into a proof format.\nQuestion:{Question}\nAnswer:{COT} |
| Translate proof problem to Lean 3 | Convert this natural langauge statement into a Lean 3 theorem statement:{Theorem} |
| Translate Lean 3 to proof problem | Convert this Lean 3 theorem statement into natural language:{STATEMENT} |
| Suggest a tactic based on Lean state | Given the Lean 3 tactic state, suggest a next tactic:\n{LEAN State} |
| Rephrase Problem | Describe this problem in another way. {Question} |
| Augment Problem | Please augment a new problem based on: {Question} |
| Augment a harder Problem | Increase the complexity of the problem: {Question} |
| Change specific numbers | Change specific numbers: {Question} |
| Introduce fractions or percentages | Introduce fractions or percentages: {Question} |
| Code Interpreter | lagent |
| In-context Learning | Question:{Question}\nAnswer:{COT}\n...Question:{Question}\nAnswer:{COT} |
Please refer to InternLM.
Our model is still under development and will be upgraded. There are some possible issues of InternLM-Math. If you find performances of some abilities are not great, welcome to open an issue.
- Jump the calculating step.
- Perform badly at Chinese fill-in-the-bank problems and English choice problems due to SFT data composition.
- Tend to generate Code Interpreter when facing Chinese problems due to SFT data composition.
- The reward model mode can be better leveraged with assigned token probabilities.
- Code switch due to SFT data composition.
- Some abilities of Lean can only be adapted to GSM8K-like problems (e.g. Convert chain-of-thought to Lean 3), and performance related to Lean is not guaranteed.
To be appended.