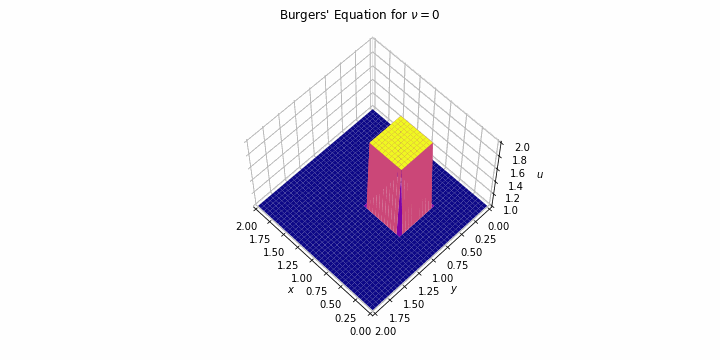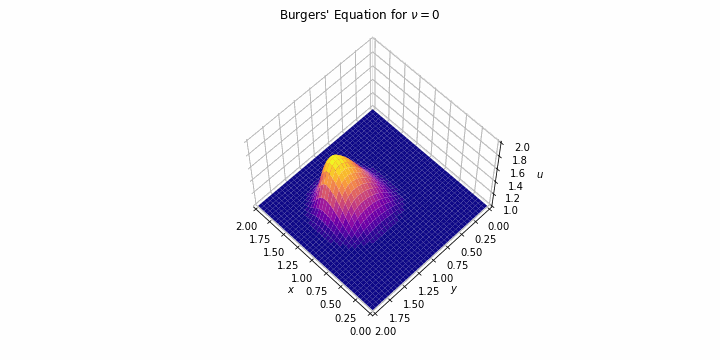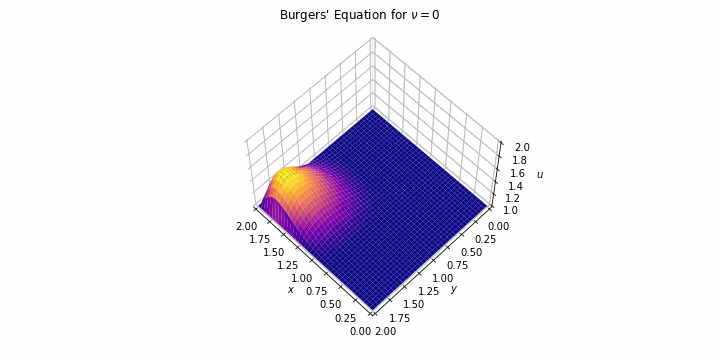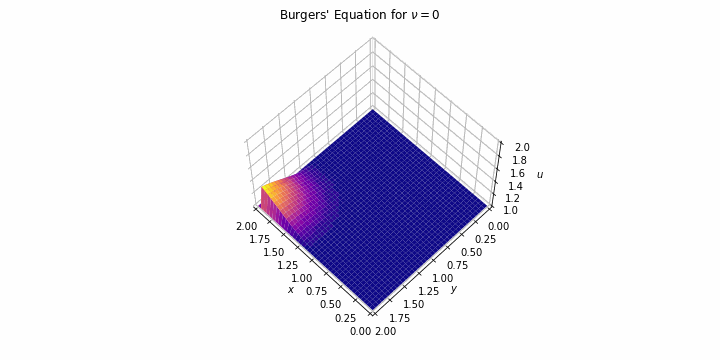
The Burgers' equation or Bateman-Burgers' equation was first introduced in 1915 and later studied in 1948 as a simplification of the Navier-Stock equation to understand its main mathematical properties such as the tendency of the viscous term to cero or the nonlinerity of the convective.
Navier-Stokes equation (1):
Thus, the Burgers' equation neglects the pressure and gravity terms from
(1)transforms it into a quasi-linear parabolic PDE. We
have written down the expanded equation for 2D Cartesian coordinates below assuming
that and letting
:
Burgers' Equation:
And this is the equation we are solving for two particular situations: first, we
solve it for a high value of the kinetic viscosity and, second, we drop that
value making the convective source predominates until the shocks appears. All of
that using a python script and the libraries numpy and matplotlib within
a beautiful animated plot.