osick/the-trapped-knight

Python library to solve the "trapped knight problem"

The Trapped Knight Problem Solver

Table of Contents

=================

• The Problem
  • Examples
• The Python Libary
  • Requirements
  • Installation
  • The Classes
    • Class spiralBoard
    • Class knightPathFinder
    • Class pathAnimation
  • Sample Usage
  • The main file
• Licence
• References

The Problem

The trapped knight problem is the following: Think of an infinite chess board where the squares are labeled according to the following pattern:

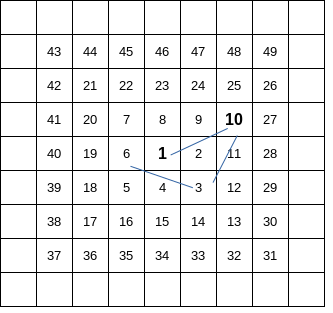
The squares are numbered along a spiral starting at one and circling around it until infnity.

Next put a knight on the 1 square of this spiral chess board and ask for the path of the knight according to the following two rules

1. never go to a square were the knight has been before
2. Go to the square with minimum integer label.

In the situation above starting at the 1 the next square is 10.

This problem can be generalized to other types of knights, not only hopping in (1,2) steps on the board, but with arbitrary step patterns (x,y) (with x>0 and y>0). It is importantt to notice the problem can be simplified to the situtation where gcd(x,y)==1. In the case gcd(x,y)==c>1 this can be simplified to the case (x/c,y/c) withput loss of generality. Of course we also have the same resulty for the (y,x)-knight compared to the (x,y)-knight.

Questions are now?

1. How long is ths path?
2. Can it be infinite?

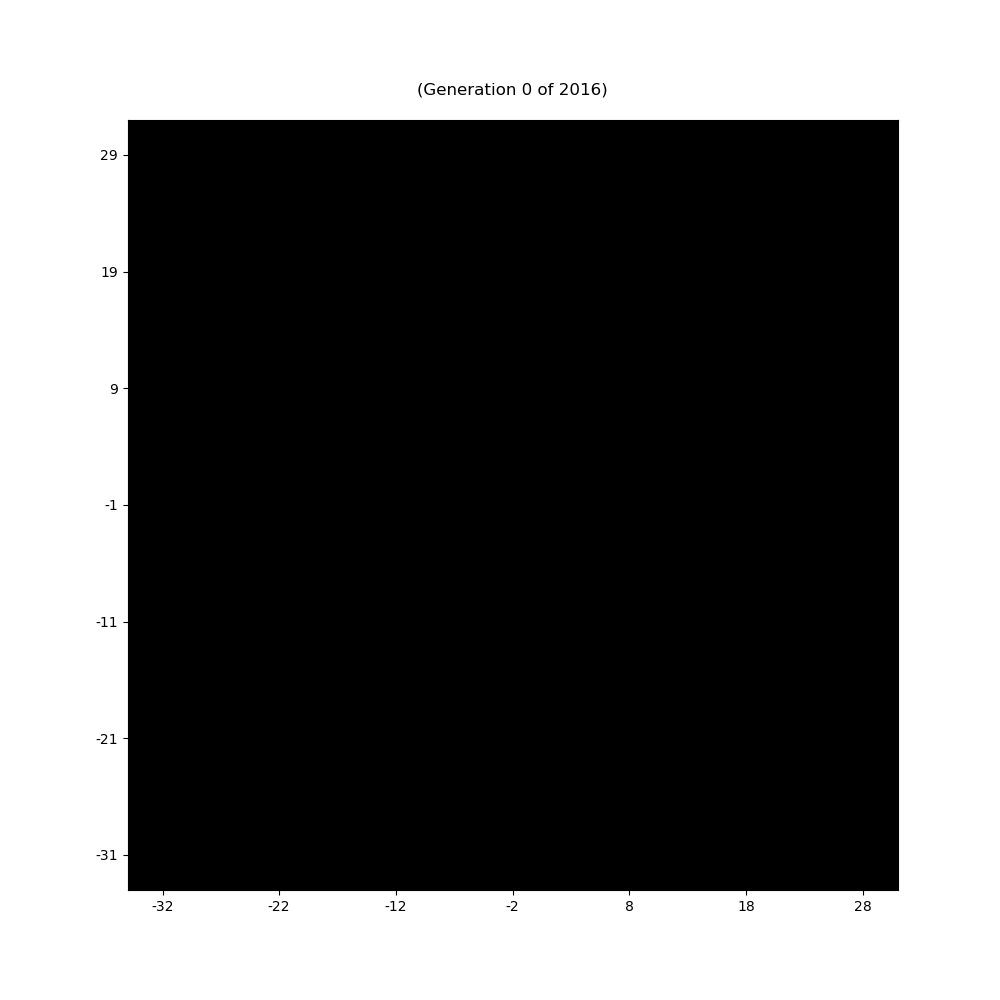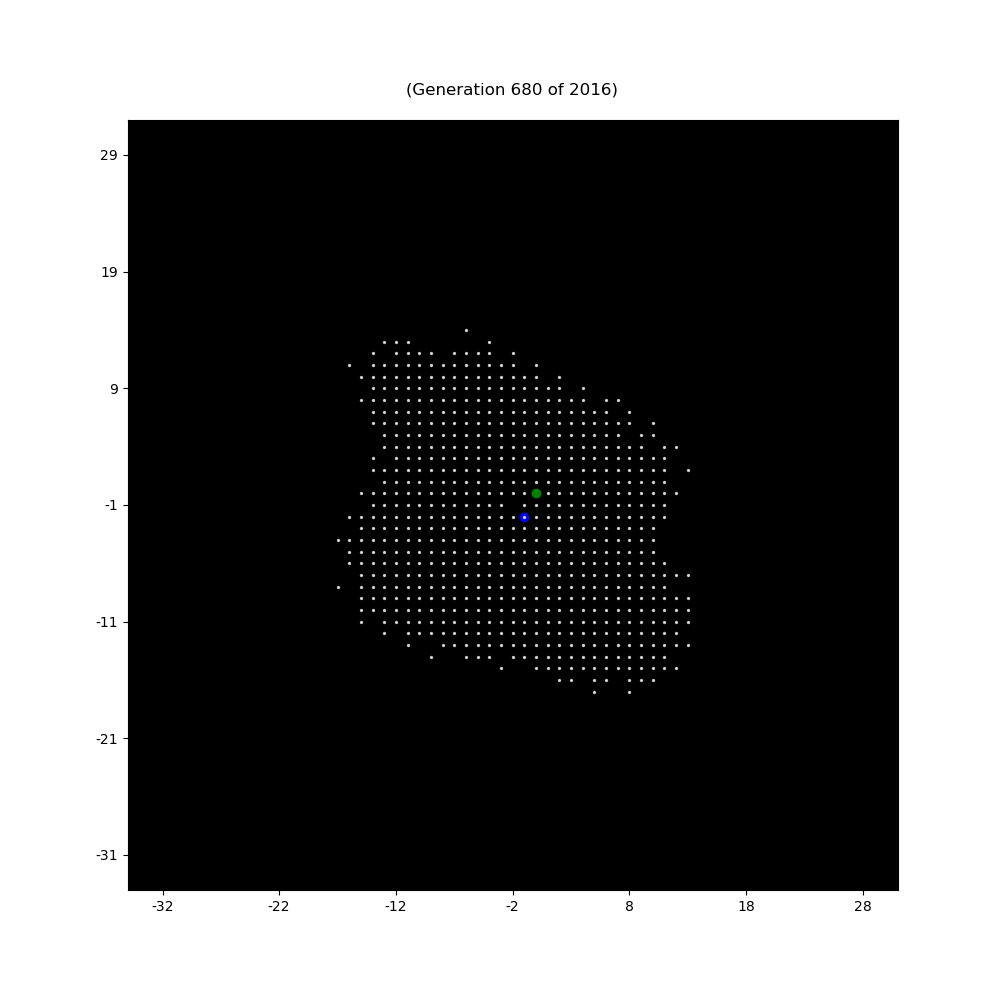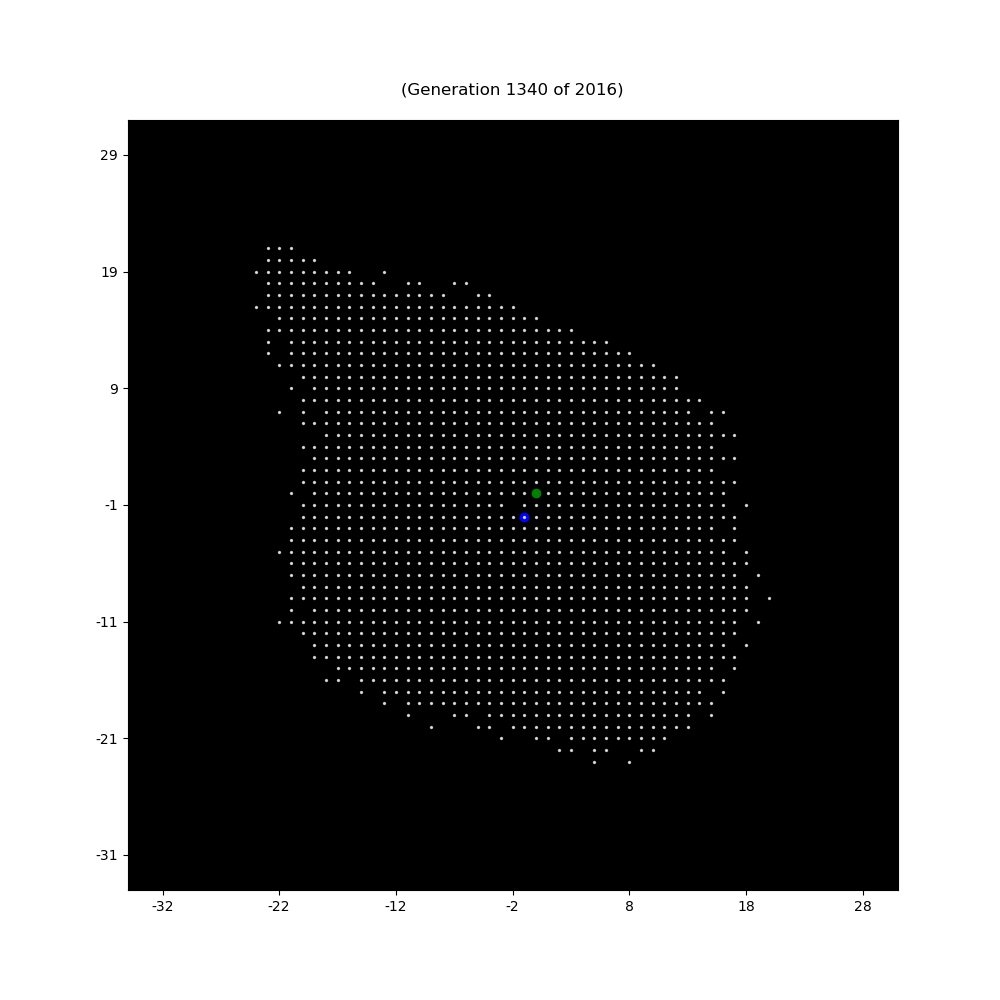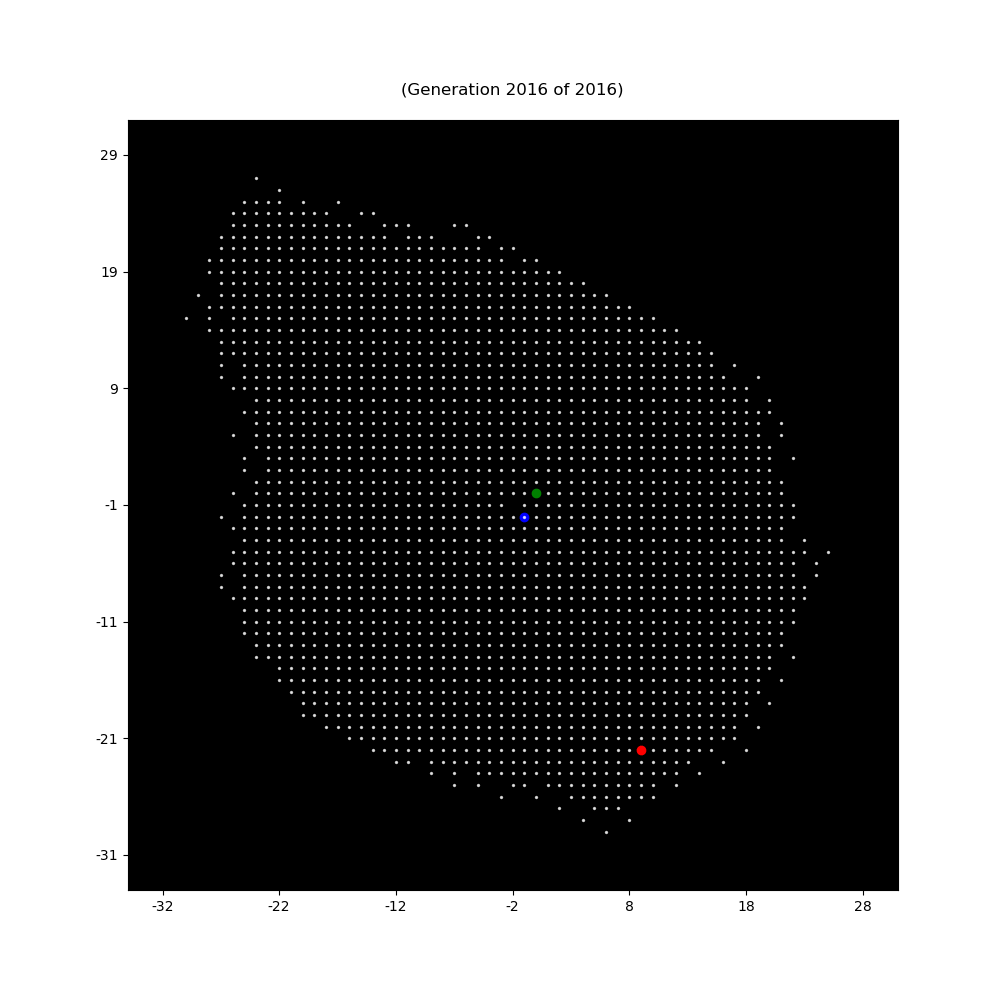
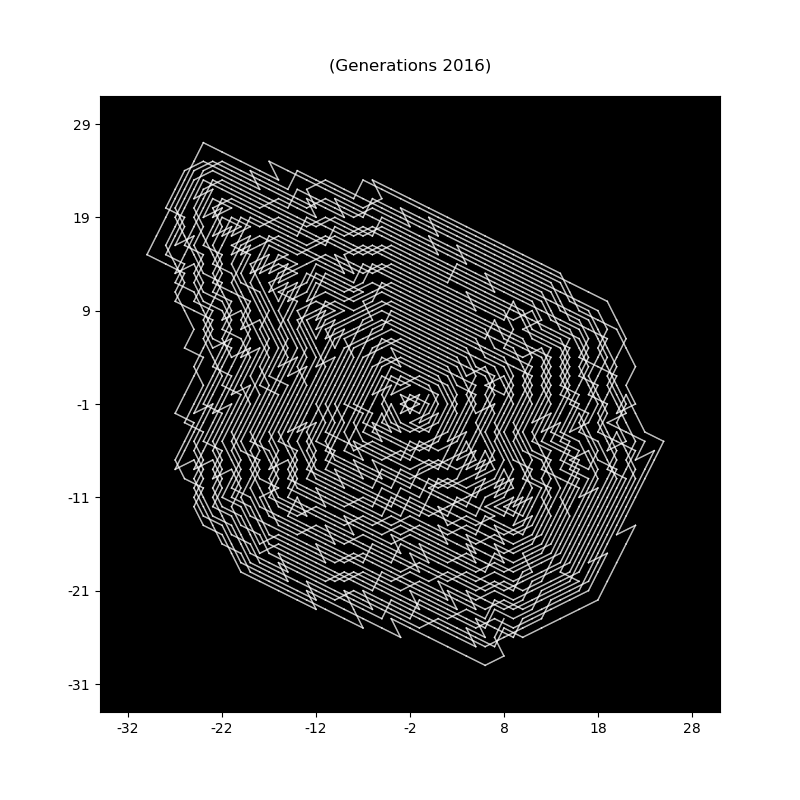
For a (1,2)-knight the path has length 2016, for other types of knight we have the following sample data (computed using this library):

Type of knight	Length	xDiam	yDiam	Density
(1,2)-knight	2016	55	56	0.65455
(1,3)-knight	3723	92	91	0.44470
(1,4)-knight	13103	125	125	0.83859
(2,1)-knight	2016	55	56	0.65455
(2,3)-knight	4634	81	81	0.70629
(3,1)-knight	3723	92	91	0.44470
(3,2)-knight	4634	81	81	0.70629
...	...	...	...	...
...	...	...	...	...
(17,22)-knight	27154	277	278	0.35262
(17,23)-knight	9051	230	220	0.19766
(18,23)-knight	27430	277	283	0.34991
...	...	...	...	...

The meaning of the values is

• Length is path length
• xDiam is the maximum diameter of the path in x-direction
• yDiam is the maximum diameter of the path in y-direction
• Density is the ratio Length/(xDiam*yDiam) which is always <=1. The density expresses the degreaa of foldedness of the path.

Up to now no (x,y)-knight is known with infinite path length

Examples

All examples are generated using this library (in fact using the main.py, see below).

• An MP4 for the (1,22)-knight
• A gif for the (1,2)-knight
  
• A HTML file for the (2,5)-knight
• more to come

The Python Library

Requirements

The source is a Python 3 library using

• Numpy
• Matplotlib
• Ffmpeg
• imagemagick

Installation

1. Download the the file theTrappedKnight.py from this repository
2. Copy it into your working directory.
3. Done

The Classes

Class spiralBoard

tbd

Class knightPathFinder

tbd

Class pathAnimation

tbd

Sample Usage

• A basic example script using this library may look like this:

  #!/usr/bin/env python3
  # -*- coding: utf-8 -*-
  
  # Import the three classes
  from theTrappedKnight import spiralBoard, knightPathFinder, pathAnimation 
  
  # Generate a spiral board
  mySpiralBoard  = spiralBoard()
  
  # Together with x,y geometry pass the board to the 
  # knightPathFinder class (here for the (1,2)-knight)
  myKnightPathFinder  = knightPathFinder(sb.squares, [1,4])
  
  # Generate the spiral path of the Knight
  myKnightPathFinder.genHistory()
  # The genHitory() method has a rudimentary output of some data of the path.
  # In this case we will get the command line output 
  # "Knight path of shape (1,2) , Length = 2016 , xDiam = 55 , yDiam = 56 , Density = 0.65455"
   
  # Define a new pathAnimation Class passing a knightPathFinder instance to it
  myPathAnimation=pathAnimation(myKnightPathFinder)
  
  # Animate the Path
  myPathAnimation.animate(outputType="animgif", color="white", speed=100, outDir="out", type="scatter")

• We are done! The result is

The main file

main.py is a reference implementation of the library and can be used to generate data and graphical representantions of the problem. We have

Usage:
      Python main.py <num> <num>-... [screen|mp4|avi|animgif|gif|html|data] [line|scatter]
      or
      Python main.py <num>-<num> <num>-<num> [screen|mp4|avi|animgif|gif|html|data] [line|scatter]

Further Thoughts

tbd

Licence

GPL v3.0

References

• The problem will be explained in detail at Numberphile
• On OEIS the length is computed for a large quantity of x,y-knights (aka x,y-leapers)