The Standard Normal Distribution - Lab

Introduction

In the previous lesson, you learned about the formula of the $z$-score, and looked at a few toy examples to explain an observation's standard score for normally distributed data. In this lab, you'll practice by standardizing and visualize some normal distributions.

Objectives

You will be able to:

Calculate and interpret the z-score (standard score) for an observation from normally distributed data
Visualize data before and after standardization to visually inspect the results

Let's get started

A $z$-score can help identify how many standard deviations above or below the mean a certain observation is. Every time you obtain a $z$-score, use “above” or “below” in your phrasing.

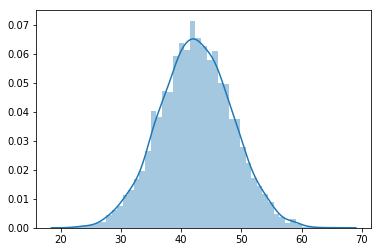
The yields of apple trees in an orchard have been recorded in the file yield.csv. Each observation is recorded by weighing apples from trees (in pounds) and adding their weights. There are 5000 observations in total for this data.

Load, visualize and give general comments about the dataset

Use pandas for loading and inspecting the data.

# Import libraries

# Read the yield data as a dataframe

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}

</style>

	0
0	39.741234
1	39.872055
2	44.331164
3	46.600623
4	40.694984

# Create a plot

# Your comments about the data here

Briefly explain what each value represents in this data set

# Your answer here

Define the interval bounds which contain 99% of the observations

Hint: Recall the empirical rule related to $3\sigma$.

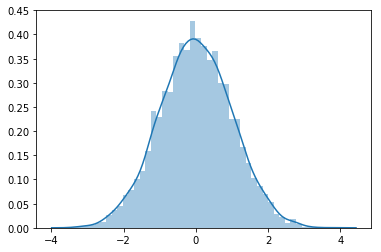
# Perform any calculations necessary here

# Write your answer here

Compute and interpret the z-score for a tree yielding 35 pounds of apples

# Calculate z

# Interpret the result

Suppose a tree has a z-score of 1.85. Interpret this z-score. What is the yield of this tree?

# Interpret the z score

# Calculate yield

# What is the yield ?

Convert each tree’s yield to a z-score so the new variable is the “z-score for weight”

The units are still the apple trees. For the data set of all z-scores:

What is the shape?
The mean?
The standard deviation?

# Give your solution here

Mean: 0.0
SD: 1.0

# Your observations

Summary

In this lab, you practiced your knowledge of the standard normal distribution!

ovilar/dsc-standard-normal-distribution-lab