evoltree is a novel Multi-objective Optimization (MO) approach to evolve Decision Trees (DT) using Grammatical Evolution (GE), under two main variants: a pure GE method (EDT) and a GE with Lamarckian Evolution (EDTL). Both variants evolve variable-length DTs and perform a simultaneous optimization of the predictive performance (measured in terms of AUC) and model complexity (measured in terms of GE tree nodes). To handle big data, the GE methods include a training sampling and parallelism evaluation mechanism. Both variants both use PonyGE2 as GE engine, while EDTL uses sklearn DT.
Solutions are represented as a numpy.where expression in the format bellow, with x being a pandas dataframe with data; idx a column from the dataset; comparison a comparison signal (e.g., <, ==); value being a numerical value; and result can be another numpy.where expression (creating chained expressions), or a class probability (numeric value from 0 to 1). Due to this representation, current evoltree implementation only allows numerical attributes.
numpy.where(x[<idx>]<comparison><value>,<result>,<result>) Example of a generated Python code (left) and the corresponding DT (right):

More details about this work can be found at: https://doi.org/10.1016/j.eswa.2020.114287.
Using pip:
pip install evoltreeThis short tutorial contains a set of steps that will help you getting started with evoltree.
evoltree package includes two example datasets for testing purposes only. Data is ordered in time and the second dataset contains events collected after the first one. To load the datasets, already divided into train, validation and test sets, two functions were created:
- load_offline_data - returns the training, validation and test sets from first dataset, used for static environments;
- load_online_data - returns the training, validation and test sets from both datasets, used for online learning scenarios.
Next steps present how to load data in the two different modes (online and offline). Due to privacy issues, all data is anonymized.
# Import package
from evoltree import evoltree
# Create evoltree object
edt = evoltree()
# Loading first example dataset, already divided into train, validation and test sets.
X, y, X_val, y_val, X_ts, y_ts = edt.load_offline_data()
# Loading both example datasets, already divided into train, validation and test sets.
X1, y1, X_val1, y_val1, X_ts1, y_ts1, X2, y2, X_val2, y_val2, X_ts2, y_ts2 = edt.load_online_data()
print(X)
print(y)# Outputs
## X (train)
col1 col2 col3 col4 col5 col6 col7 col8 col9 col10
0 0.755951 4.653432 2.767041 0.739897 0.101081 2.401580 2.890712 3.157321 5.554321 0.865465
1 5.624979 4.782823 0.416159 0.823179 0.101081 2.446735 0.739841 2.564807 4.552277 0.991334
2 0.755951 5.365407 3.081596 0.739897 0.101081 3.174113 1.986985 3.193263 3.378832 0.865465
3 4.436114 6.393779 0.416159 0.823179 0.101081 2.238128 2.066007 2.564807 3.436435 0.865465
4 7.071106 6.069200 0.416159 0.739897 0.101081 5.100103 0.739841 3.551982 4.886248 0.991334
... ... ... ... ... ... ... ... ... ... ...
708937 0.755951 4.804125 0.416159 0.823179 0.101081 2.807017 2.066007 2.564807 5.802875 0.865465
708938 0.755951 2.558737 0.416159 0.823179 0.101081 2.558737 2.066007 2.564807 5.802875 2.173501
708939 0.755951 2.875355 0.416159 0.823179 0.101081 2.572643 0.739841 2.455024 2.947305 0.991334
708940 0.755951 4.694221 0.416159 0.823179 0.101081 3.568007 0.739841 2.455024 6.279122 0.991334
708941 6.631839 2.553551 0.416159 0.823179 0.101081 2.446735 0.739841 2.564807 5.266229 0.991334
[708942 rows x 10 columns]
[708942 rows x 10 columns]
## y (train)
0 NoSale
1 NoSale
2 NoSale
3 NoSale
4 NoSale
...
708937 NoSale
708938 NoSale
708939 NoSale
708940 NoSale
708941 NoSale
Name: target, Length: 708942, dtype: object
Next steps present the basic usage of both variants (EDT and EDTL) for modeling the previously loaded data in an offline environment.
# Imports
from sklearn import metrics
from sklearn.tree import DecisionTreeClassifier
from evoltree import evoltree
import matplotlib.pyplot as plt
# Create two evoltree objects, one for each variant
edt = evoltree()
edtl = evoltree()
# Load dataset
X, y, X_val, y_val, X_ts, y_ts = edt.load_offline_data()
# Fit both versions on train data
## Normal variant:
edt.fit(
X,
y,
"Sale",
X_val,
y_val,
pop=100,
gen=10,
lamarck=False,
experiment_name="test",
)
y_pred1 = edt.predict(X_ts, mode="best")
## Lamarckian variant, doesn't need as much iterations (gen)
edtl.fit(
X,
y,
"Sale",
X_val,
y_val,
pop=100,
gen=5,
lamarck=True,
experiment_name="testLamarck",
)
# Predict on test data, using the solution with better predictive performance on validation data
y_predL1 = edtl.predict(X_ts, mode="best")
# Fit a traditional Decision Tree for comparison
dt = DecisionTreeClassifier(random_state=1234).fit(X, y)
prob = dt.predict_proba(X_ts)
# Compute AUC on test data
fpr, tpr, th = metrics.roc_curve(y_ts, y_pred1, pos_label="Sale")
fprL1, tprL1, thL1 = metrics.roc_curve(y_ts, y_predL1, pos_label="Sale")
fprdt, tprdt, thdt = metrics.roc_curve(y_ts, prob[:, 1], pos_label="Sale")
auc1 = metrics.auc(fpr, tpr)
aucL1 = metrics.auc(fprL1, tprL1)
aucdt = metrics.auc(fprdt, tprdt)
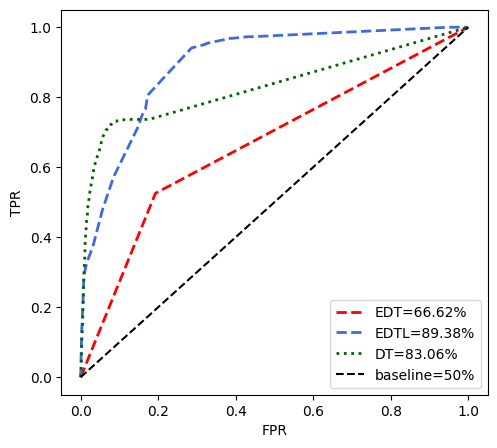
# Plot results
plt.rcParams["font.family"] = "sans-serif"
fig, ax = plt.subplots(1, 1, figsize=(5.5, 5))
plt.plot(
fpr,
tpr,
color="red",
ls="--",
lw=2,
label="EDT={}%".format(round(auc1 * 100, 2)),
)
plt.plot(
fprL1,
tprL1,
color="royalblue",
ls="--",
lw=2,
label="EDTL={}%".format(round(aucL1 * 100, 2)),
)
plt.plot(
fprdt,
tprdt,
color="darkgreen",
ls=":",
lw=2,
label="DT={}%".format(round(aucdt * 100, 2)),
)
plt.plot([0, 1], [0, 1], color="black", ls="--", label="baseline=50%")
plt.legend(loc=4)
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.show()
plt.savefig("results.png")Result:
If you use evoltree for your research, please cite the following paper:
Pedro Jose Pereira, Paulo Cortez, Rui Mendes:
Expert Systems with Applications 168: 114287 (2021).
@article{DBLP:journals/eswa/PereiraCM21,
author = {Pedro Jos{\'{e}} Pereira and Paulo Cortez and Rui Mendes},
title = {Multi-objective Grammatical Evolution of Decision Trees for Mobile Marketing user conversion prediction},
journal = {Expert Systems with Applications},
volume = {168},
pages = {114287},
year = {2021},
doi = {10.1016/j.eswa.2020.114287},
}