随机森林实现与优化报告

郑钊 15331424 计算机应用
2018-07-15

[TOC]

1. 实验简介

1.1. 开发环境

Intel(R) Core(TM) i7-5557U
8.00 GB RAM
Windows 10 Pro
Visual Studio 2017

1.2. 运行程序

使用 VS2017 打开 random-forest.sln。
修改 main.cpp 中下列三者为相应的路径。

TRAIN_DATA_PATH：训练数据文件的路径
TEST_DATA_PATH：测试数据文件的路径
PREDICT_DATA_PATH：测试结果文件的路径

设置 main.cpp 中的训练参数。

tree_num：CART 总数
max_depth：CART 最大深度
feature_total：特征总数
random_sample_num：每次随机抽取样本的数目
random_feature_num：每次随机抽取特征的数目
node_sample_num_threshold：CART 节点样本数目的最小值

推荐的参数为：

rf.tree_num = 16;
rf.max_depth = 8;
rf.feature_total = 201;
rf.random_sample_num = 65536;
rf.random_feature_num = 128;
rf.node_sample_num_threshold = 8;

菜单栏 -> 调试 -> 开始执行(不调试)。
最终输出的预测结果文件在 PREDICT_DATA_PATH 对应的路径

2. 实现

2.1. 随机森林原理

随机森林是一种典型的树集成算法，是基于不同的样本、不同的特征训练出 N 颗 CART。本次实验项目虽然是一个二分类的问题，但是由于 Kaggle 上要求的是预测测试样本为正的概率，所以我们这次实验要构造的 CART 不是分类树，而是回归树。随机森林对 N 颗 CART 的回归结果取均值作为最终的预测概率。

CART（分类回归树）是一种二分决策树（既能是分类树，又能是分类树）。其在构建的过程中，每次对特征进行切分后只会产生两个子节点，CART 分裂时：

如果 CART 是分类树，采用 GINI 值作为节点分裂的依据；
如果 CART 是回归树，采用样本的最小方差作为节点分裂的依据。

上面已经说了，我们要构造的是 CART 回归树，所以在分裂节点的时候参考的依据是样本的最小方差。

2.2. 训练算法

随机抽取 n 个样本
随机抽取 k 个特征
基于 1, 2 抽取的样本、特征，训练出一颗 CART
对于 k 个特征，找出每个特征的最佳分裂点以及对应分裂后的样本均方差
选择分裂后样本均方差最小的特征进行分裂
重复 1, 2 直到：

+ 节点的深度达到预设的最大深度 `max_depth`
+ 节点中的样本数目小于预设的阈值 `node_sample_num_threshold`
+ 分裂后的样本均方差大于或等于分裂前的样本方差（没必要再分裂）

重复 1, 2, 3 直到训练出预设数量的 CART 集合

2.3. 代码设计

基于数据结构 X, Y, Sample 和 Node，在 RandomForest 中构造 CART 集合。

2.3.1. 数据结构

typedef vector<float> X;

typedef bool Y;

typedef struct {
  X x;
  Y y;
} Sample;

struct Node {
  int feature;
  float value;
  float split_point;
  Node *left;
  Node *right;

  Node() {
    feature = -1;
    value = false;
    split_point = 0.0f;
    left = NULL;
    right = NULL;
  }

  bool is_leaf() const {
    return left == NULL && right == NULL;
  }
};

2.3.2. CART

struct CART {
  Node *root;

  // constructor
  CART() {
    root = NULL;
  }

  // classify
  float classify(const X &x) const {
    Node *node = root;
    while (!node->is_leaf()) {  // while not a leaf node
      if (node->left == NULL) node = node->right;
      else if (node->right == NULL) node = node->left;
      else node = x[node->feature] <= node->split_point ? node->left : node->right;
    }
    return node->value;
  }
};

2.3.3. RandomForest

class RandomForest {

public:
  // params
  int tree_num;                          // CART 总数
  int max_depth;                         // CART 最大深度
  int feature_total;                     // 特征总数
  int random_sample_num;                 // 每次随机抽取样本的数目
  int random_feature_num;                // 每次随机抽取特征的数目
  int node_sample_num_threshold;         // CART 节点样本数目的最小值

  // public methods
  void train                             // 训练
    (const vector<Sample> &train_samples);
  float predict                          // 预测
    (const X &x);

private:
  // train data
  vector<Sample> train_samples;          // 训练样本
  vector<int> sample_indices;            // 训练样本索引（用于随机抽取样本）
  vector<int> feature_indices;           // 特征索引（用于随机抽取特征）
	
  // models
  vector<CART> carts;                    // CART 集合

  // private methods
  vector<Sample*> random_select_samples  // 随机抽取 random_sample_num 个样本
    (void);
  vector<int> random_select_features     // 随机抽取 random_feature_num 个特征（0~200）
    (void);
  CART generate_cart                     // 训练一颗 CART
    (vector<Sample*> &samples, vector<int> &features);
  void split_node_recursively            // 递归地分裂节点
    (vector<Sample*> &samples, vector<int> &features, Node *&node, const int depth);
  tuple<float, float> find_split         // 找到一组特征中的最佳分割点
    (vector<Sample*> &samples, const int feature);
  float compute_variance                 // 计算样本方差
    (const vector<Sample*> &samples);
  void sort_on_feature                   // 将样本基于某个特征进行排序
    (vector<Sample*> &samples, const int feature);
};

3. 并行优化

3.1. 非并行版本

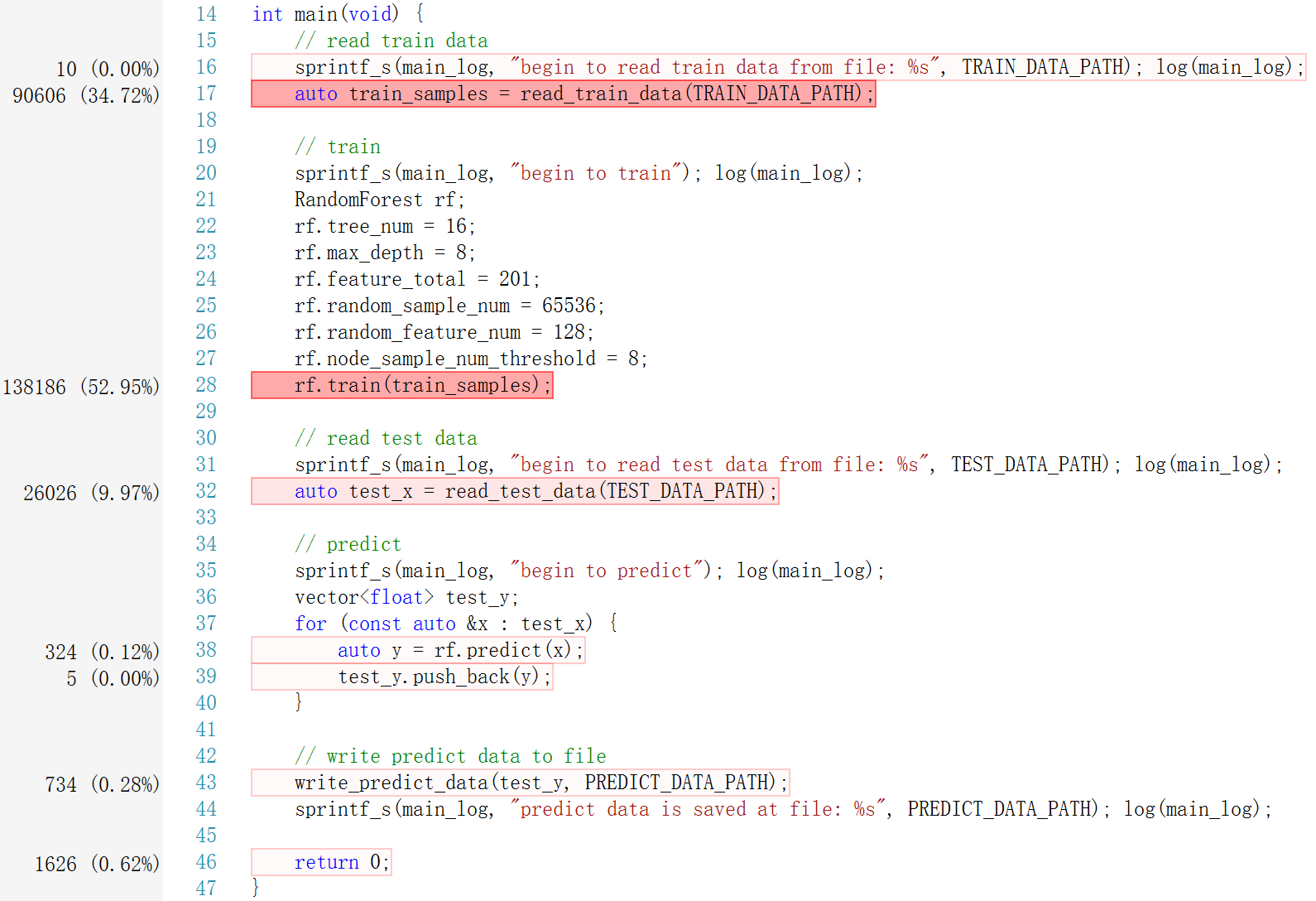
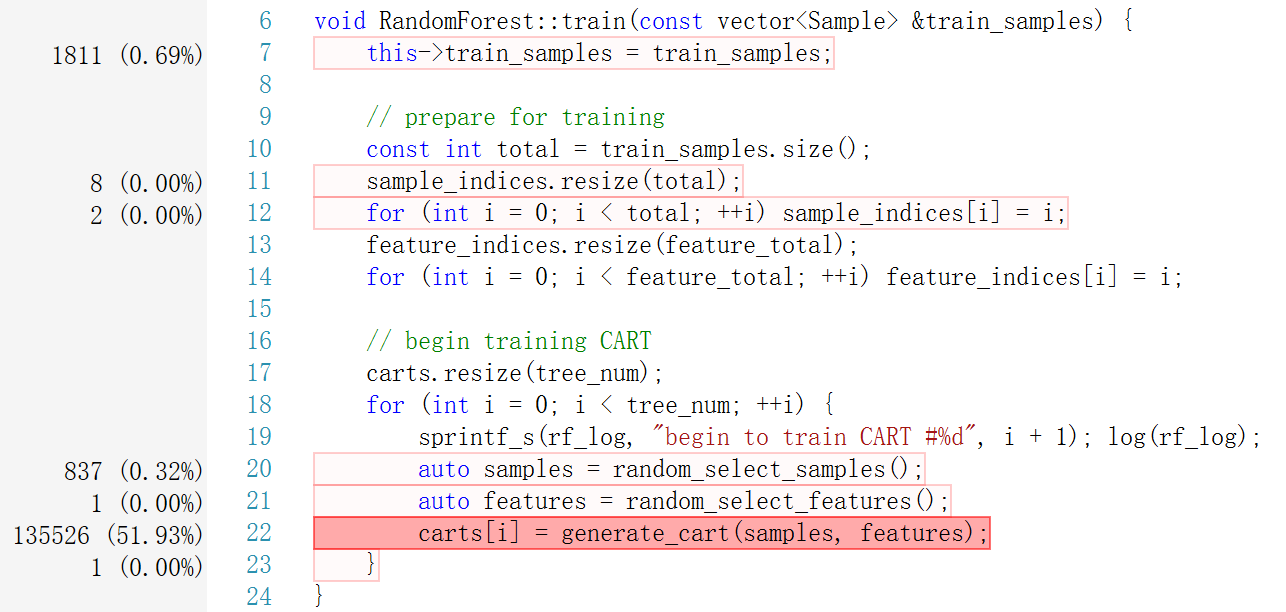
可以看到，整个程序的运行，除去读取数据的时间消耗之外，绝大多数的时间用在 train 上。

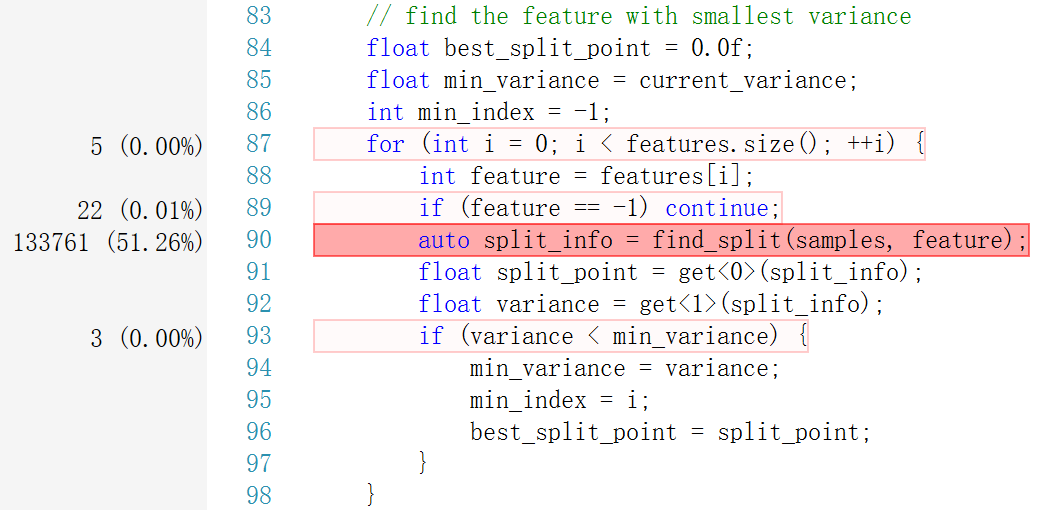
在 train 中，近一半的时间用于寻找最佳分割点 find_split。另外，值得一提的是，由于我是通过深度优先的方式构建 CART，随意分裂左节点消耗的时间会多于分裂右节点。

3.2. 并行优化

并行化分析：

随机森林最大的特点就是 CART 之间是两两独立的，所以并行化的第一个思路就是并行地生成每一颗 CART。
另外，在生成每一颗 CART 的过程中，每个特征找最佳分割点的过程，也可以并行化。

3.2.1. 并行生成 CART

omp_set_num_threads(4);
#pragma omp parallel for
for (int i = 0; i < tree_num; ++i) {
  sprintf_s(rf_log, "CART #%d begin to train in thread #%d", i + 1, omp_get_thread_num()); log(rf_log);
  auto samples = random_select_samples();
  auto features = random_select_features();
  carts[i] = generate_cart(i + 1, samples, features);
}

开始训练，这里对比一下非并行化版本、4-thread 和 8-thread 的区别：

对比非并行化版本和 4-thread 可以发现：在并行化前后的 CPU 使用率和训练时间差别很大，并行化能带来约 50% 的训练速度提升！
对比 4-thread 和 8-thread 可以发现：后者的性能提升相比较于前者并不明显，因此没有必要开 8-thread。

3.2.2. 并行寻找最佳分割点

#pragma omp parallel for
for (int i = 0; i < features.size(); ++i) {
  int feature = features[i];
  if (feature == -1) continue;
  auto split_info = find_split(samples, feature);
  float split_point = get<0>(split_info);
  float variance = get<1>(split_info);
  if (variance < min_variance) {
    min_variance = variance;
    min_index = i;
    best_split_point = split_point;
  }
}

这里优化之后，对训练时间的优化几乎可以忽略，这是因为前面 3.2.1 中的并行优化已经饱和了。

4. Cache 友好优化

这里在代码中的体现主要是通过样本索引的打乱来体现的，优化之后性能上的提升也是几乎可以忽略不计的，这里就不展示。

void shuffle(vector<int> &cards) {
  srand(time(NULL));
  int n = cards.size();
  for (int i = 0; i < n; ++i) {
    int index = rand() % (n - i) + i;
    if (index != i) {
      int tmp = cards[i];
      cards[i] = cards[index];
      cards[index] = tmp;
    }
  }
}

vector<Sample*> RandomForest::random_select_samples(void) {
  vector<Sample*> samples;

  // shuffle
  shuffle(sample_indices);

  const int total = train_samples.size();
  const int begin = rand(0, total);
  for (int i = 0; i < random_sample_num; ++i) {
    int j = sample_indices[(begin + i) % total];
    samples.push_back(&train_samples[j]);
  }

  return samples;
}

5. 预测结果

之前基于 xgboost 的 Kaggle 得分：0.89812
本算法的 Kaggle 得分：0.87472

painterdrown/random-forest