bait - Büchi Automata Inclusion Tester

A ω-regular language inclusion checker.

bait - Büchi Automata Inclusion Tester

Introduction

bait is an ω-regular language inclusion checker which relies on an algorithm derived from Abstract Interpretation techniques. The tool accepts as input two ω-regular languages represented as Büchi automata and outputs whether the inclusion holds or not. The automata are represented with the the .ba format.

bait is the implementation of an algorithm presented at the conference CONCUR in 2021. A link to the article is given here.

Prerequisites

Java 8+

Building and Running

Use ./gradlew build to build bait.

The easiest way to run bait is to execute the bait.jar file with java -jar bait.jar -a path/to/A.ba -b path/to/B.ba. You can download it from the release page. Alternatively, you can build the jar file with:

git clone https://github.com/parof/bait
cd bait
./gradlew installDist

This command will build the executable .jar file in build/libs. Once you built the executable you can run:

java -jar build/libs/bait.jar -a path/to/A.ba -b path/to/B.ba

You can also run bait using gradlew run:

./gradlew run --args='-a /path/to/A.ba -b /path/to/B.ba'

Run with argument --help to see the all the available options.

The `.ba` format

The input automata must be specified in the .ba format. The official description of the format, written by its authors, has been archived here. Other tools, for example RABIT, accept the same input format. One .ba file must respect the following specification:

(initial state)
...
(transitions)
...
(accepting states)

Observe that automata in .ba format have only one initial state. One state is simply a sequence of characters. Here there are some examples:

state
state1
a
iB
[0][1][2]

Observe that [0][1][2] is a single state: the squared brackets are just part of the name of the state and they don't have a semantic meaning. Additionally, we require that the states don't include in the names the strings , or ->, because they will be used to define the transitions.

One transition is defined as

symbol,firstState->secondState

where symbol is a sequence of characters, and firstState and secondState are states. Similarly to the states, the symbols can't contain -> or , as substrings. Here there are some examples of valid transitions:

a,s1->s2
1,s->s'
sym,[0][0]->[0][1]

If no initial state is specified, the first state in the first transition of the automaton is considered to be the initial one. If no final state is specified, then each state in the automaton is considered to be final.

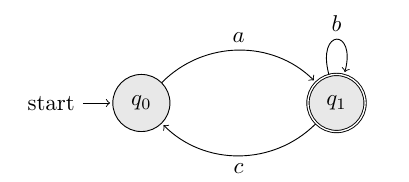
Consider the following automaton:

It can be represented in the .ba format as:

q0
a,q0->q1
b,q1->q1
c,q1->q0
q1

Observe that since the initial state is also the first state of the first transition, and then we can omit to specify it:

a,q0->q1
b,q1->q1
c,q1->q0
q1

Working example

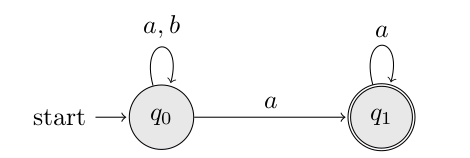
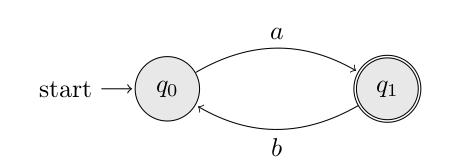
We want to compute whether the inclusion holds between the following automata:

The first automaton A is represented in the .ba format as:

a,q0->q0
b,q0->q0
a,q0->q1
a,q1->q1
q1

While the second automaton B is represented in the .ba format as:

a,q0->q1
b,q1->q0
q1

You can finally compute whether the inclusion holds or not using bait.jar with the following command:

java -jar bait.jar -a A.ba -b B.ba

This command will give you the following output:

Since the language of A is (a+b)*aω and the language of B is (ab)ω the inclusion doesn't hold, and then False is correctly returned.

Benchmarks

In the test-automata directory there are some examples of automata in the .ba format. We benchmarked bait with a large set of automata, and they can be found in a separate repository: https://github.com/parof/buchi-automata-benchmark.

parof/bait