This repo provides pip package stratx for the StratPD and CatStratPD algorithms for computing model-independent partial dependence. With 0.4 release, we added feature impact and importance.
Source is Python 3 and license is MIT.
Partial dependence curves (FPD) introduced by Friedman (2000), are an important model interpretation tool, but are often not accessible to business analysts and scientists who typically lack the skills to choose, tune, and assess machine learning models. It is also common for the same partial dependence algorithm on the same data to give meaningfully different curves for different models, which calls into question their precision. Expertise is required to distinguish between model artifacts and true relationships in the data.
In this paper, we contribute methods for computing partial dependence curves, for both numerical (StratPD) and categorical explanatory variables (CatStratPD), that work directly from training data rather than predictions of a model. Our methods provide a direct estimate of partial dependence, and rely on approximating the partial derivative of an unknown regression function without first fitting a model and then approximating its partial derivative. We investigate settings where contemporary partial dependence methods—including FPD, ALE, and SHAP methods—give biased results. Furthermore, we demonstrate that our approach works correctly on synthetic and plausibly on real data sets. Our goal is not to argue that model-based techniques are not useful. Rather, we hope to open a new line of inquiry into nonparametric partial dependence.
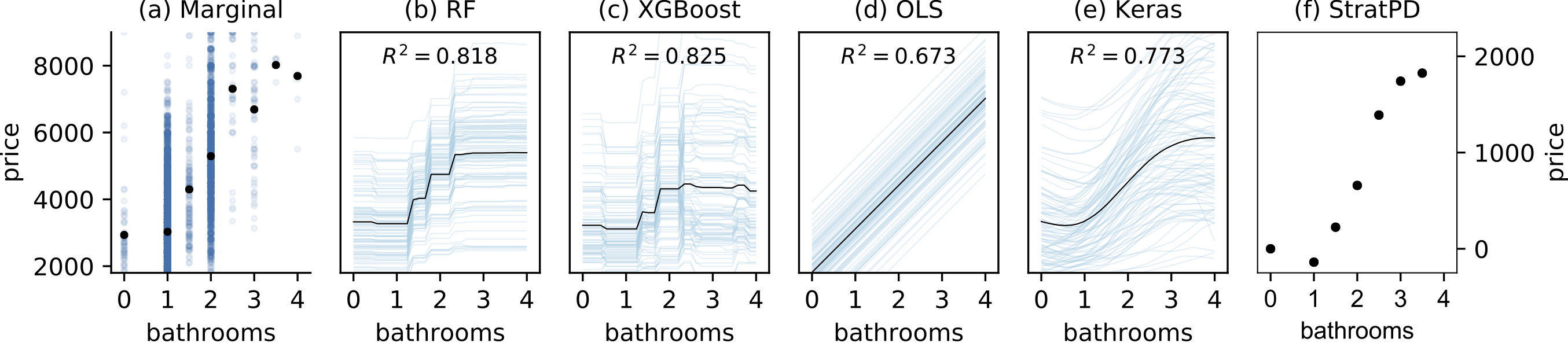
See the academic paper, written with James D. Wilson, but the basic problem is that the same algorithm, operating on the same data, can give meaningfully different partial dependences depending on the model chosen by the user. Consider the following comparison of Friedman's partial dependence plots and ICE plots for 3 different models to the StratPD version.
(Plots of bathrooms versus rent price using New York City apartment rent data. Sample size is 10,000 observations of ~50k. The PD/ICE plots are radically different for the same data set, depending on the chosen user model. Hyper parameters were tuned using 5-fold cross validation grid search over several hyper parameters. Keras model trained by experimentation: single hidden layer of 100 neurons, 500 epochs, batch size of 1000, batch normalization, and 30% dropout. StratPD gives a plausible roughly result that rent goes up linearly with the number of bathrooms. R2 were computed on 20% validation sets.)
See the academic paper, written with James D. Wilson and Jeff Hamrick.
Practitioners use feature importance to rank and eliminate weak predictors during model development in an effort to simplify models and improve generality. Unfortunately, they also routinely conflate such feature importance measures with feature impact, the isolated effect of an explanatory variable on the response variable. This can lead to real-world consequences when importance is inappropriately interpreted as impact for business or medical insight purposes. The dominant approach for computing importances is through interrogation of a fitted model, which works well for feature selection, but gives distorted measures of feature impact. The same method applied to the same data set can yield different feature importances, depending on the model, leading us to conclude that impact should be computed directly from the data. While there are nonparametric feature selection algorithms, they typically provide feature rankings, rather than measures of impact or importance. They also typically focus on single-variable associations with the response. In this paper, we give mathematical definitions of feature impact and importance, derived from partial dependence curves, that operate directly on the data. To assess quality, we show that features ranked by these definitions are competitive with existing feature selection techniques using three real data sets for predictive tasks.
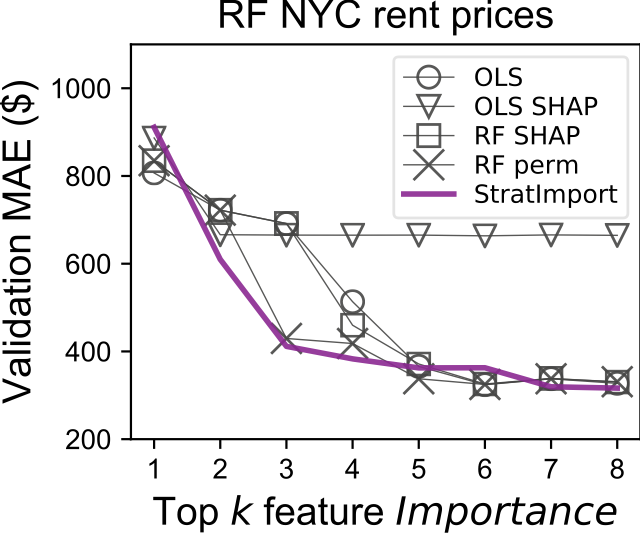
Sorry. I don't have examples set up yet for feature impact except for those images needed for the paper. Here are the top k features from a NYC rent data set training an RF model and comparing the mean absolute error:
Latest is 0.4.
pip install -U stratxSee notebooks/examples.ipynb for lots more stuff.
from sklearn.datasets import load_boston
from stratx.partdep import *
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
X = df.drop('MEDV', axis=1)
y = df['MEDV']
# WORKS ONLY WITH DATAFRAMES AT MOMENT
plt.figure(figsize=(3.5,3.5))
plot_stratpd(X, y, 'LSTAT', 'MEDV', yrange=(-20, 5), n_trials=10)
plt.tight_layout()
plt.show()
from sklearn.datasets import load_diabetes
from stratx.partdep import *
diabetes = load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
df['y'] = diabetes.target
X = df.drop('y', axis=1)
y = df['y']
plt.figure(figsize=(3.5,3.5))
plot_stratpd(X, y, 'bmi', 'y', n_trials=10)
plt.tight_layout()
plt.show()
diabetes = load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
df['sex'] = np.where(df['sex']<0, 0, 1)
df['y'] = diabetes.target
X = df.drop('y', axis=1)
y = df['y']
plt.figure(figsize=(3.5,3.5))
plot_catstratpd(X, y, 'sex', 'y',
show_x_counts=False,
n_trials=10,
min_y_shifted_to_zero=True,
catnames=['female','male']) # not sure which is male/female actually!
plt.tight_layout()
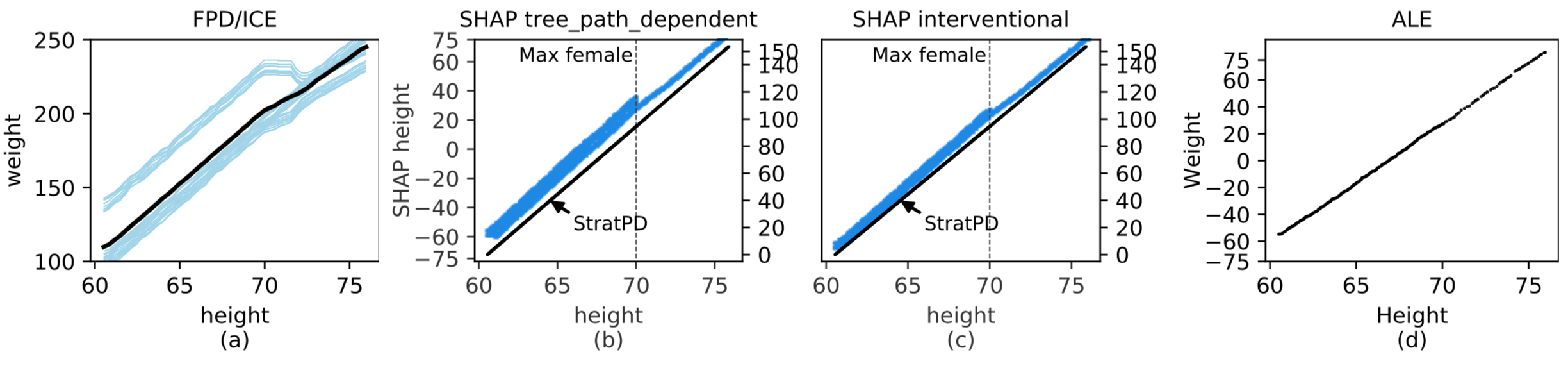
plt.show() 
Plots of height versus weight using synthetic data body weight data (see academic paper). The PD/ICE on the left is biased by codependent features since pregnant women, who are typically shorter than men, have a jump in weight.
