The Hilbert crate implements the highly efficient Skilling algorithm for performing the Hilbert curve transformation and its inverse for points in two dimensions on up to points with thousands of dimensions in Rust. The original algorithm in C may be found in this conference article:
"Programming the Hilbert curve" by John Skilling. AIP Conference Proceedings 707, 381 (2004); https://doi.org/10.1063/1.1751381
Researchers have discovered many uses for the Hilbert Curve, including:
- Speeding up K-Nearest neighbor search
- Unassisted, high-dimensional clustering
- Data compression
- Pseudo-random number generation
- Processing Lidar point clouds
- Database query optimization
- Approximate traveling salesman solutions
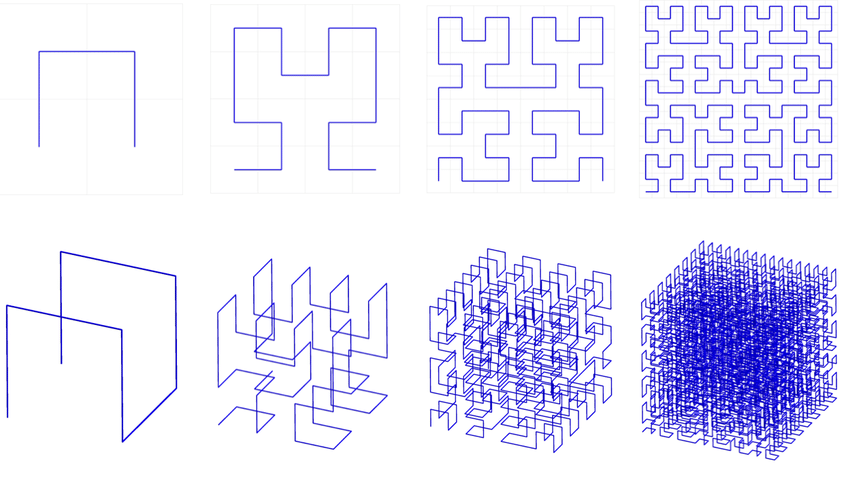
The 1st Three Iterations of the HILBERT CURVE
╔════════════╗ ╔═════╗ ╔═════╗
║ ║ ║ ║ ║ ║
║ ║ ║ ╚════╝ ║
║ ║ ║ ║
║ ║ ╚═════╗ ╔═════╝
║ ║ ║ ║
║ ║ ║ ║
══════╝ ╚══════
1 iteration 2 iterations
╔════╗ ╔════╗ ╔════╗ ╔════╗
║ ║ ║ ║ ║ ║ ║ ║
║ ║ ║ ║ ║ ║ ║ ║
║ ╚════╝ ║ ║ ╚════╝ ║
║ ║ ║ ║
║ ║ ║ ║
╚════╗ ╔════╝ ╚════╗ ╔════╝
║ ║ ║ ║
║ ║ ║ ║
╔════╝ ╚══════════════╝ ╚════╗
║ ║
║ ║
║ ╔═════════╗ ╔═════════╗ ║
║ ║ ║ ║ ║ ║
║ ║ ║ ║ ║ ║
╚════╝ ╔════╝ ╚════╗ ╚════╝
║ ║
║ ║
╔════╗ ╚════╗ ╔════╝ ╔════╗
║ ║ ║ ║ ║ ║
║ ║ ║ ║ ║ ║
║ ╚═════════╝ ╚═════════╝ ║
3 iterations
Skilling's algorithm can perform the transformation in time linearly proportional to D (the number of dimensions) and B (the number of bits required to encode each coordinate.) This performance is greatly superior to most if not all other algorithms in the literature when dealing with high dimensional points (anything over a half dozen dimensions).
This library offers the following features:
- Forward Hilbert Curve transformation from a D-dimensional point to a 1-dimensional index (represented as a
BigUint). See thefast_hilbertmodule. Points may have anywhere from two to thousands of dimensions. - Inverse Hilbert Curve transformation from a 1-dimensional
BigUintindex back to a D-dimensional point. See thefast_hilbertmodule. - D-dimensional points whose Euclidean distance formula has been optimized, making it suitable for use in K-nearest neighbor searches. See the
Pointclass. Thehilbert_sortmethod sorts points according to the Hilbert Curve. - Data normalization routines to prepare input data so that a Hilbert transform may be applied to it. See the classes
IntegerDataRangeandFloatDataRange. Thenormalizeandcompressmethods can translate and scale the input data and coerce it into the unsigned values that the Hilbert transform requires. - Permutation logic, for generating alternate Hilbert curves for the same data. See the
Permutationclass.
To run the benchmarks:
> cargo bench
The benchmarks rely upon the criterion crate, which functions best if you install gnu-plot. If it is installed and findable on the path, it will write a report here:
hilbert\target\criterion\report\index.html
Here are examples using the crate:
- Create two 3-D points and get the square of the distance between them.
- Perform the Hilbert Transform on a single point.
- Create several points and normalize them.
- Sort the points by the Hilbert Curve, using 11 bits per dimension.
- Round trip, showing how to convert a point to the Hilbert index and back again.
// 1. Create two 3-D points and get the square of the distance between them.
let p1 = Point::new(0, &[3, 4, 5]);
let p2 = Point::new(1, &[0, 8, 10]);
let sqr_dist = p1.square_distance(&p2);
assert!(sqr_dist == 50, "Square distance should be 50");
// 2. Perform the Hilbert Transform on a single point,
// using 5 bits per dimension (which assumes no coordinate exceeds 31).
let index1 = p1.hilbert_transform(5);
// 3. Create several points and normalize them.
// This will ensure that the ids begin at zero and that all values
// are multiplied by 10.0 before being rounded to the nearest integer,
// to preserve the predetermined precision.
let point_data : Vec<Vec<f64>> = vec![
vec![-10.5, 5.27, 3.66],
vec![-4.802, 20.2, 100.19],
vec![42.0, -100.0, 0.0]
];
let (mut points, bits) = point_list::make_points_f64(&point_data, 0, None, None, 10.0);
// 4. Sort the points by the Hilbert Curve, using 11 bits per dimension,
// because the range of data is 200.19, multiplied by the scale of 10
// yields 2001.9, ceiling of that yields 2002, which is between 1024 (2^10)
// and 2048 (2^11), so 11 bits are required to store the
// highest coordinate value.
Point::hilbert_sort(&mut points, 11);
// 5. Round trip, from point to Hilbert index and back.
let p1 = Point::new(0, &[3, 4, 5]);
let index = p1.hilbert_transform(5);
let p2 = Point::new_from_hilbert_index(0, &index, 5, 3);