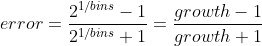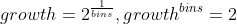Quantogram accepts a stream of floating point numbers (f64) with optional weights and estimates the desired quantile, such as the median, as well as providing other common measures like count, min, max, mean and mode. The caller may tradeoff storage and accuracy by choosing the desired absolute relative error from this range:
- lowest accuracy = 17.2%
- default accuracy = 1.0%
- highest accuracy = 0.034%
Add this to your Cargo.toml:
[dependencies]
quantogram = "0.4"
then you are good to go.
The library requires Rust's 2021 edition, but only so that it can run benchmarks against the zw-fast-quantile library, which requires that version. You could build from source and remove the benchmarks related to ZW if you need the 2018 edition.
See the change log for changes: Change log
The default configuration is adequate for most uses and promises a 1% worst-case error rate.
Default Quantogram with Unweighted Samples
This example creates a default Quantogram, adds some samples, and computes the count, min, max, mean, median, and third quartile (75% quantile). It also removes some samples and repeats the median.
use quantogram::Quantogram;
let mut q = Quantogram::new();
q.add(10.0);
q.add(40.0);
q.add(20.0);
q.add(30.0);
q.add(50.0);
assert_eq!(q.count(), 5);
assert_eq!(q.min().unwrap(), 10.0);
assert_eq!(q.max().unwrap(), 50.0);
assert_eq!(q.mean().unwrap(), 30.0);
assert_eq!(q.median().unwrap(), 30.0);
assert_eq!(q.quantile(0.75).unwrap(), 40.0);
q.remove(10.0);
q.remove(20.0);
assert_eq!(q.median().unwrap(), 40.0);Use QuantogramBuilder to set accuracy
This example creates a Quantogram using a QuantogramBuilder, sets its accuracy to 0.5%, adds a list of samples in bulk, and computes the median.
use quantogram::{QuantogramBuilder,Quantogram};
let mut q = QuantogramBuilder::new()
.with_error(0.005)
.build();
let data = vec![10.0,40.0,20.0,30.0,50.0];
q.add_unweighted_samples(data.iter());
assert_eq!(q.median().unwrap(), 30.0);Working with Weighted Samples
This example begins by adding unweighted samples (which are assigned a weight of one) then adds in a heavily weighted zero sample.
use quantogram::{Quantogram};
let mut q = Quantogram::new();
let data = vec![1.0,2.0,3.0,4.0,5.0,95.0,96.0,97.0,98.0,99.0];
q.add_unweighted_samples(data.iter());
q.add_weighted(0.0, 6.0);
assert_eq!(q.median().unwrap(), 2.0); Dealing with Gaps in data
If there is a large gap in the data at the point where the desired quantile falls, it is proper to average the value below and above the gap to get the quantile. The median and quantile methods do not attempt this, but fussy_quantile does. For example, the following sequence has an even number of elements, so the median is supposed to be the average of the two middle values, 5 and 95, yielding 50, a number not even close to any of the values in the set:
Samples = { 1,2,3,4,5,95,96,97,98,99 }
use quantogram::{Quantogram};
let mut q = Quantogram::new();
let data = vec![1.0,2.0,3.0,4.0,5.0,95.0,96.0,97.0,98.0,99.0];
q.add_unweighted_samples(data.iter());
assert_eq!(q.fussy_quantile(0.5, 2.0).unwrap(), 50.0); The upper limit on storage required for the highest accuracy is 500x that of the lowest accuracy and 29x that of the default accuracy. One can choose any value for error rate that falls in the range above.
The storage is affected by how many histogram bins each power of two range of values is divided into. Few bins gives a coarse result while many bins gives a fine result. Storage is linearly proportional to the number of bins chosen.
The growth factor indicates that each bin is wider than the previous bin in an exponential way.
For example, if bins is 35 then growth is 1.02 and error is 1%.
| Bins | Error Rate |
|---|---|
| 2 | 17.2 % |
| 3 | 11.5 % |
| 4 | 8.6 % |
| 5 | 6.9 % |
| 7 | 4.9 % |
| 12 | 2.9 % |
| 18 | 1.9 % |
| 35 | 1.0 % |
| 70 | 0.5 % |
| 139 | 0.25% |
| 347 | 0.10% |
| 694 | 0.05% |
| 867 | 0.04% |
| 1000 | 0.0347% |
To halve the error rate you need to double the number of bins (and double the storage).
The maximum storage requirement is approximately this (setting aside a few configuration properties in the structure and overhead imposed by the Skip Dictionary):
storage = (2 x 8-byte floats) x (2 x 254 x (bins + 1) + 7)
≈ 8 kb x (bins + 1)
The 2 x 254 has 2 for positive and negative values and 254 for the number of powers of two between the smallest and largest magnitude numbers supported by 64-bit floats. The bins + 1 is because there are two histograms, a coarse histogram that just collects one count for the nearest power of two and a fine histogram that divides each power of two into bins separate counts.
However, if samples never go above a million and are only recorded to three decimal places, the 254 in the formula above could be reduced to 31.
The range of maximum storage required goes from 25 KB for 2 bins to 8.2 MB for 1000 bins. For the default of 35 bins at 1% accuracy, the storage max is about 300 KB. However, if only positive integers from one to a million were added, this would drop to 17 KB. Drop the accuracy to 5% and the memory required drops to 3.5 KB. Thus you have much flexibility in tuning the structure to achieve your goals. (Fewer bins and lower accuracy also leads to faster performance.)
Any quantile. Some algorithms require you to choose the target quantile before you start collecting the data. This structure permits the querying of any quantile and does not require you to configure it to target any particular range of phi.
Extreme Quantiles. Some algorithms lose accuracy when dealing with extreme quantiles (values near zero or one) and may compensate by increasing storage. Quantogram's accuracy guarantee applies to all values for phi, the desired quantile. Also, its storage requirements do not change to accommodate extreme quantiles.
Weighted Samples. Samples may be uniformly weighted (weight = 1) or be assigned separate weights, so that weighted medians and weighted quantiles may be computed.
Remove Samples. Samples may be removed and the quantiles will be updated to reflect this.
Warning: If the minimum or maximum value is removed, subsequent requests for the minimum or maximum (until a new extreme sample is added) may return an incorrect value.
Descriptive Statistics. Quantogram provides these basic statistics:
- min
- max
- mean
- median
- variance
- standard deviation
- quantile
- q1, q3 (1st and 3rd quartiles)
- mode
- hsm (half-sample mode)
- count
Notes:
- The standard deviation (stddev) calculates the population standard deviation, not the sample standard deviation.
- If only integer values are collected, the
modewill be rounded to the nearest integer. - If integer values in the range [-63,63] are used, a good value for mode will result.
- If non-integer values are collected or integers outside this range, then the effect of non-uniform histogram bin widths will distort the
modeand the anwswer will not be what you expect. Bins vary in size exponentially, so themodewill act like the mode of the log of the samples. This will skew themodetoward larger values, as larger numbers are part of larger bins. - Most rules of thumb related to the use of histograms to estimate the mode (like Sturges' Rule and Scott's Rule) use bin counts that are much lower than what is used by
Quantogram. It might be better to rebin by consolidating multiple adjacent bins in order to compute themode. - As an alternative to the mode, try the half-sample mode,
Quantogram::hsm. This applies a generalized form of the Robertson-Cryer (1974) half-sample mode estimator to histogrammed data instead of the raw samples. It has been generalized from the algorithm by David Bickel to apply to weighted samples. The half-sample mode is good at ignoring outliers and contamination. - The half-sample mode (
hsm) as implemented is worse than quadratic in performance (possiblyO(N² Log N)). To compensate for this, a cache has been added that often recalculates thehsmover a subset of the data in the neighborhood of the previously calculated mode.- If new values are added that are within this neighborhood, partial recalc will be done. If the Quantogram uses buckets with growth of 1.02 (for 1% quantization error) then the default neighborhood of 70 bins covers the range
[1/2 x mode, 2 x mode]. If a distribution has a well-defined peak, this core region should often include the newly added sample and permit the optimization. - If new values are outside the neighborhood, it is unlikely that they will move the mode. Permit reuse of previously computed mode without any recalc for a dozen samples in a row before forcing a full recalc.
- If the number of buckets grows too much or the change in total weight is too much, a full recalc will be done.
- If there are fewer than 64 bins, perform a full recalc. This enables a proper and accurate mode to arise from the data before the caching kicks in.
- If new values are added that are within this neighborhood, partial recalc will be done. If the Quantogram uses buckets with growth of 1.02 (for 1% quantization error) then the default neighborhood of 70 bins covers the range
Measures of Dispersion
These additional statistics are implemented which are measures of dispersion:
- range (spread between min and max)
- iqr (interquartile range: Q3 - Q1)
- quartile_deviation (semi-interquartile range, half of iqr))
- coeff_of_range ((max - min) / (max + min))
- coeff_of_quartile_dev ((Q3-Q1)/(Q3+Q1))
- coeff_of_stddev (standard deviation divided by mean)
- coeff_of_variation
Inverse Quantile. Lookup the quantile at which a given value falls using the quantile_at function.
Exceptional Values. Infinities and NANs are counted separately and do not factor into the quantile calculation. The proportion of such values may be queried.
Overflow and Underflow. If infinitesmal values are not ineresting, the underflow value may be changed to treat values smaller than a threshold as zeroes. Likewise, an upper threshold may be set and all values larger in magnitude are considered infinities (positive or negative).
By compressing the dynamic range of recorded values, less storage is required and performance is enhanced.
Special handling of Integers. So long as only integers (samples with no fractional component) are added to the collection, requests for a quantile will round to the nearest integer.
Exact values for sparse bins. If only one value has been added to a certain bin, instead of the midpoint between the bin's lower and upper value being used, the exact sample value will be used.
Changed in version 0.3.0: If repeated additions of the same value are made and all match this accurate sample value, the accurate sample will be retained. The first differing value to be added to that bin will cause the bin's midpoint value to be used instead.
Measuring quantiles of streams of data (such as the median) is an essential basic statistic in many applications. Your choices are:
- Accurate and fast with moderate storage requirements, limited to a dense range of values like integers
- Accurate and slow with high storage requirements
- Approximate with probabilistic guarantees of accuracy, fast, and low storage requirements
- Approximate with fixed guarantees of accuracy, fast, and moderate storage requirements
Dense histogram. The first is ideal but has limited applicability. It is typically implemented using a list as a dense histogram with each bucket corresponding to an integer value. If all your samples are integers that fall beween zero and 10,000 (or are floats on a uniform grid with no more than 10,000 grid lines) it is the best choice, both easy to implement and efficient to use.
Sorted list. The second includes the naive approach, which is to gather all the data in a list, then sort it to get the quantile. To expedite, you can use quickselect so that you do not need to sort all the data. This approach does not work for streaming data, because the storage requirements are vast.
Probabilistic. The third category has algorithms (such as variations on Count Min Sketch) that guarantee a given accuracy with a certain probability. A popular median estimator is called Median of Medians. If you know how many items N there will be, you can use reservoir sampling to maintain a sample set of the data and take the median of that. However, the more extreme your quantile, the larger a subset you must keep. With these algorithms, you usually get a good estimate, but there is always a chance that you get a bad estimate. Also, given the same set of data, you may get different results; the answer is not deterministic.
Sparse Histogram. Sparse histograms can be used to reduce the storage requirements in comparison to dense histograms when large numbers of distinct samples must be handled. The reduction in storage is offset by greater expense in storage, retrieval and update. There are clever balanced tree structures that can be used for this, but some are complicated to implement. The strategy you use for sizing your bins affects the accuracy of the results. If logarithmically sized bins are used, you can guarantee the worst case absolute relative error will not exceed what is desired. Quantogram falls into this category. It is deterministic and has precise guarantees for worst case accuracy, not probabilistic ones.
Summaries are stored at three levels, enabling the algorithm to quickly home in on a small range of bins where the cumulative weights from the smallest number to the current number match the desired quantile.
- Top level: total weight for negatives, zeroes, positives, NANs, +/- Infinity
- Middle level: coarse counts, one for negatives and one for positives, to the nearest power of two
- Bottom level: fine counts for all finite values
The coarse and fine counts are stored in skip maps (dictionaries built upon a skip list). They are a tree-structured index into a linked list, where keys are stored in sorted order. This makes search, insert, update and ordered iteration fast.
By using the coarse counts in the middle level, one can sum up the weights to get near the quantile and discover which power of two range contains the quantile. Then the skip map's filtered iterator provides rapid access to that range of values in the fine dictionary.
Fast hashing. An important part of the algorithm is how samples are hashed to find their keys at the coarse and fine levels. At the coarse level, frexp is used to get the power of two and sign of the number, using an intrinsic math function instead of the math library log. At the fine level, the remaining mantissa is fed to an approximate log function to get the bin number. The approximate log uses a third-order Padé Approximant, which is twice as fast as the math library log.
Two use cases were examined, one dominated by insertion and the other by the quantile computation.
Insertion Heavy. A million random values were added to a naive list and a Quantogram, then a single median was taken. In release mode, the Quantogram took 2.2x as long as the naive, but with dramatically lower storage. Only 577 bins actually used, which is 1/866 as much space as the naive algorithm used.
The insertion heavy scenario strongly favors the naive algorithm, because insertion is its strength, whereas the quantile computation requires a sort, but is only performed once.
Quantile Heavy. 20,000 random values were added to a naive list and a Quantogram, with a median taken after each insertion. In release mode, the Quantogram was 65x faster than the naive approach. As the number of samples increases, this ratio should improve further.
Profiling reveals that the bulk of the time is spent performing operations on the SkipMap.
Comparison to Other Crates
The quantiles Crate has an implementation of the algorithm from Cormode, Korn, Muthukrishnan, and Srivastava's paper "Effective Computation of Biased Quantiles over Data Streams".
The zw-fast-quantile crate implements the Zhang Wang Fast Approximate Quantiles Algorithm.
All are tuned to an error of 1%.
Scenario #1: Query with each insertion
Quantogramgrows linearly with the number of insertions and quantile requests- CKMS seems to grow as N Log N.
- By the time you reach 50,000 insertions and queries,
Quantogramis 30x faster than CKMS and 489x faster than ZW. - The
zw-fast-quantilereadme advertises that it is faster thanCKMS, but my benchmarking shows it is 4x slower for 1,000 samples and 10x slower thanCKMSfor 10,000 samples. Compared toQuantogram,ZWis 7.5x slower at 1,000 samples and 118x slower at 50,000 samples.
Quantogram is much faster than either competing crate at querying, and as the volume of data increases, the disparity grows.
Scenario #2: Insertion Alone
Quantogram falls between ZW and CKMS for insertion speed, but the ZW advantage declines as the sample count increases. At 100,000 samples, the ratio is Quantogram being 2.26x slower than ZW, which is comparable to results for inserting into a list with the naive case.
Conclusion:
Quantogram scales gracefully as the number of samples increases, which neither of the other two crates do. ZW's speed at insertion is more than offset by poor performance at querying.
Furthermore, ZW cannot handle floats directly. You must wrap them in an Ordered struct to be able to use them in its collection.
> cargo bench
...
test bench_insert_010000_qg ... bench: 1,480,556 ns/iter (+/- 180,118)
test bench_insert_010000_ckms ... bench: 7,382,904 ns/iter (+/- 641,343)
test bench_insert_010000_zw ... bench: 411,049 ns/iter (+/- 37,984)
test bench_insert_050000_qg ... bench: 6,046,822 ns/iter (+/- 539,280)
test bench_insert_050000_ckms ... bench: 111,633,379 ns/iter (+/- 7,329,546)
test bench_insert_050000_zw ... bench: 2,650,721 ns/iter (+/- 254,070)
test bench_insert_100000_qg ... bench: 12,428,788 ns/iter (+/- 3,226,464)
test bench_insert_100000_ckms ... bench: 319,816,711 ns/iter (+/- 28,905,190)
test bench_insert_100000_zw ... bench: 5,482,642 ns/iter (+/- 818,317)
test bench_median_001000_qg ... bench: 495,842 ns/iter (+/- 95,352)
test bench_median_001000_ckms ... bench: 925,006 ns/iter (+/- 85,291)
test bench_median_001000_zw ... bench: 3,809,463 ns/iter (+/- 638,667)
test bench_median_010000_qg ... bench: 3,432,471 ns/iter (+/- 537,084)
test bench_median_010000_ckms ... bench: 37,458,360 ns/iter (+/- 4,065,758)
test bench_median_010000_zw ... bench: 402,043,003 ns/iter (+/- 23,352,903)
test bench_median_050000_qg ... bench: 15,898,549 ns/iter (+/- 1,154,243)
test bench_median_050000_ckms ... bench: 491,125,737 ns/iter (+/- 18,854,159)
test bench_median_050000_zw ... bench: 7,775,610,481 ns/iter (+/- 361,052,767)
test bench_median_100000_qg ... bench: 32,615,356 ns/iter (+/- 6,294,536)
test bench_median_200000_qg ... bench: 64,630,098 ns/iter (+/- 8,511,129)
Note: Why is this use benchmark fair? A typical application will receive sensor data and then respond to it. The response requires that you compare the value to a quantile to see if it is an outlier requiring action, such as the sending of an alert. Thus calling the median or quantile method after each sample arrives is a typical use case.
- If samples are removed, several measures can become corrupted:
- min (if the current minimum value is removed)
- max (if the current maximum value is removed)
- mode (if a member of the list of current modes is removed)
- variance
- standard deviation (works in unit test, but perverse failure cases may exist)
All other measures will adapt correctly. These defects can be fixed.
-
The mode is distorted by the logarithmic size of bins. This has a tendency to cause the mode to increase. A mathematically sound correction is needed and could be implemented. Anyone know stats theory?
-
quantile_atinverse quantile measure could be further optimized to make use of the coarse bins. For 1% accuracy (35 bins per doubling), the speedup would likely be 15x in the average case. -
Weighted mean, variance and standard deviation caclulations are not protected against overflow.
-
If many values have the same weight (that differs from one, a case that is handled) then the
ModeCachecan consume an unbounded amount of memory.