Gyroid 3D Plot

The Gyroid

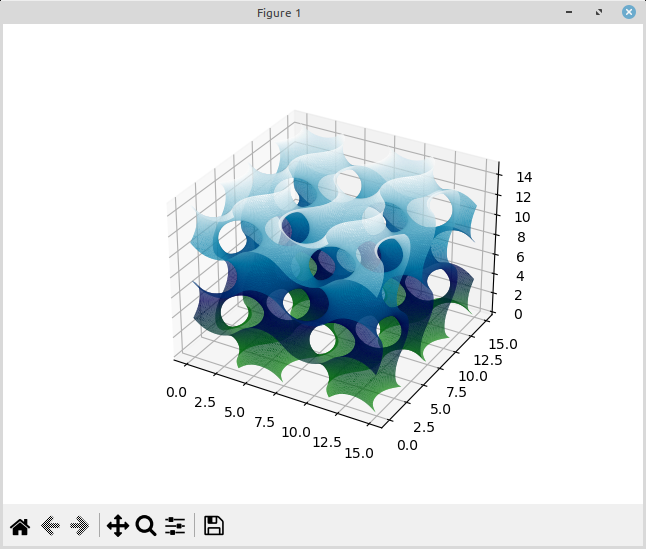
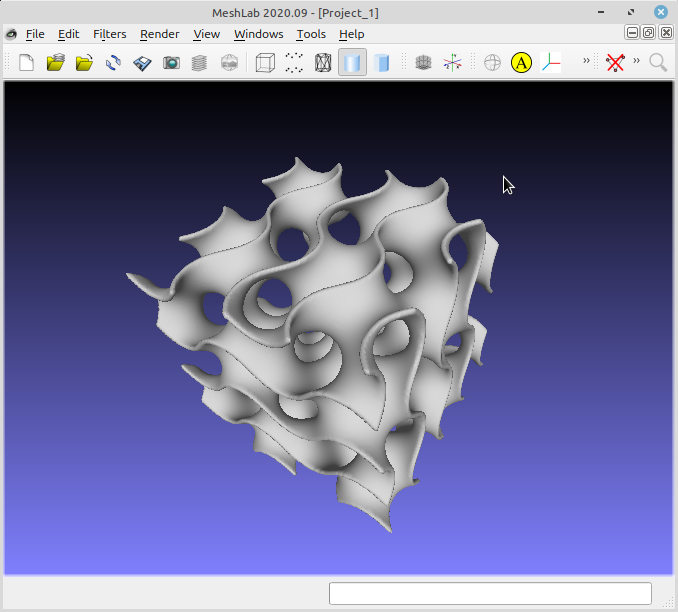
The Gyroid has become quite famous in the 3D printing community, for being often used as infill pattern.

To define a Gyroid:

Take this ℝ³→ℝ function: f(x, y, z) = cos(x) sin(y) + cos(y) sin(z) + cos(z) sin(x),
the Gyroid is the surface where f(x, y, z) = 0.

3d Surfaces - `skimage` and `matplotlib`

Such kind of ℝ³→ℝ surfaces can be hard or impossible to express as convenient and iterable parametric ℝ²→ℝ³ functions (x = f_x(u, v), y = f_y(u, v), z = f_z(u, v)).

So we are using a Python solver: vertices, faces, ... = skimage.measure.marching_cubes().
The surface can be visualized by matplotlib.pyplot.show() as done in:
```
./gyroid.py -p  # compute surface and view it
```
Visual inspection is not particularly smooth unless you have a very fast computer, so you're better off generating a volume and inspecting its STL export. See below.

Turning a 3d Surface Into a Volume - `meshlib` and `meshlab`

In order to 3D print the surface, we have to give it some volume.

To this end, we're using meshlib.mrmeshpy.offsetMesh(offset=thickness).
- Meshlib is free for education and evaluation.
- As meshlib and skimage use incompatible formats, we're saving the surface computed by the former to a temporary STL file, read by the latter.
We apply all the above and save the result as an STL file:
```
./gyroid.py -s
```
and can view the result using e.g. meshlab.
```
meshlab gyroid.stl
```

3D Printing

You can use Cura or any other slicer.

Follow this link to see a video of the successive layers.

Installation and Usage

How to Install

Make sure you have Python 3 installed.
Install the make commande. Example with Debian-based distros:
```
sudo apt install make
```
Other optional programs are meshlab and cura (or any other slicer).

For any OS having Python3, do:

make venv
. .venv/bin/activate
make require

How to Run

. .venv/bin/activate
./gyroid.py     # show options
./gyroid.py -p  # show surface in matplotlib; rotation/zoom net performant
./gyroid.py -s  # compute .stl file with thickness

Other Included Surfaces

The surfaces provided in this repo are:

Program	Description
`./gyroid.py`	The surface described above
`./lamella.py`	A surface accidentally created
`./multiple.py`	A collection of surfaces
`./organite.py`	An organic section
`./scherk-singly.py`	A Scherk surface

pbauermeister/matplotlib_gyroid