adas.utils

The goal of adas.utils is to provide some utility functions to be used in the course Analysis of Data and Statistics at the University of Trento, Italy. Course contents are on https://paolobosetti.quarto.pub/ADAS/.

Installation

You can install the development version of adas.utils from GitHub with:

# install.packages("devtools")
devtools::install_github("pbosetti/adas.utils", build_vignettes = TRUE)

Examples

Loading data sets

On https://paolobosetti.quarto.pub/data.html there are a list of example datasets to be used during the course. You can load them with the examples_url function:

examples_url("battery.dat") |> read.table(header=T) |> head()
#>   RunOrder StandardOrder Temperature Material Repeat Response
#> 1       34             1          15        1      1      130
#> 2       25             2          70        1      1       34
#> 3       16             3         125        1      1       20
#> 4        7             4          15        2      1      150
#> 5        8             5          70        2      1      136
#> 6        1             6         125        2      1       25

Chauvenet’s criterion

The Chauvenet’s criterion is a method to identify possible outliers in a sample. Here is an example:

x <- rnorm(100)
x[50] <- 10
chauvenet(x)
#> Chauvenet's criterion for sample x
#> Suspect outlier: 50, value 10
#> Expected frequency: 5.61978810813674e-11, threshold: 0.5
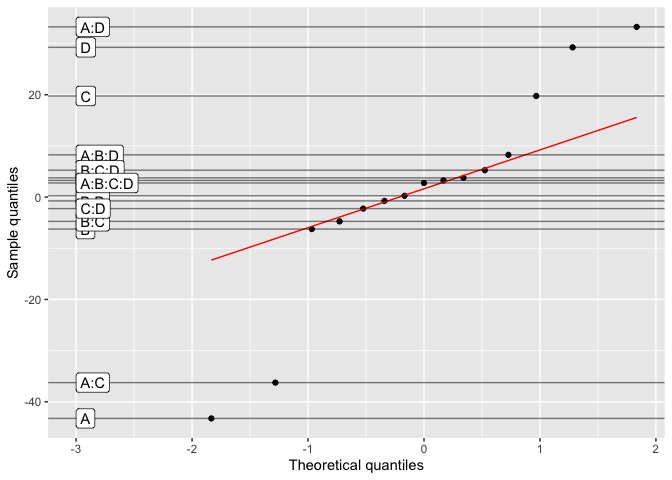
#> Decision: reject it

Daniel’s plot

Daniel’s plot is a QQ plot of the effects of a non-replicated factorial model. Here is an example:

daniel_plot_qq(lm(Y~A*B*C*D, data=filtration))

Pareto chart

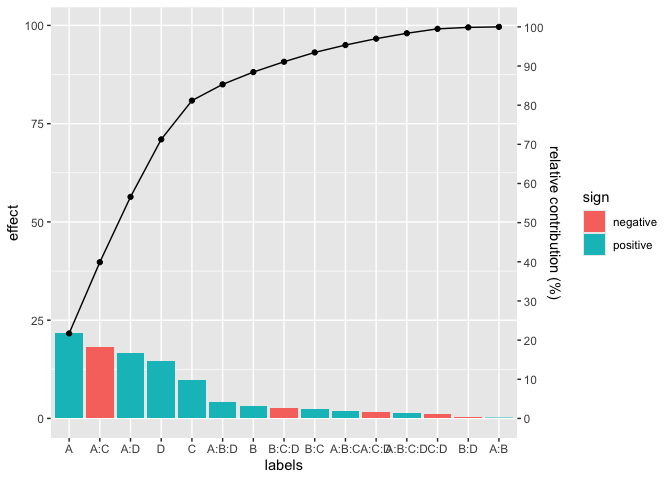
The pareto_chart function is a generic function that creates a Pareto chart either from a general data frame or from the effects of a lm object. Here is an example:

library(tidyverse)
#> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr     1.1.4     ✔ readr     2.1.5
#> ✔ forcats   1.0.0     ✔ stringr   1.5.1
#> ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
#> ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
#> ✔ purrr     1.0.2     
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ tidyr::extract()   masks magrittr::extract()
#> ✖ dplyr::filter()    masks stats::filter()
#> ✖ dplyr::lag()       masks stats::lag()
#> ✖ purrr::set_names() masks magrittr::set_names()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
set.seed(1)
tibble(
  val=rnorm(10, sd=5),
  cat=LETTERS[1:length(val)]
  ) %>%
  pareto_chart(labels=cat, values=val)

# For a linear model:
pareto_chart(lm(Y~A*B*C*D, data=filtration))

Design of Experiments

There is a host of functions to be used in the context of Design of Experiments. Here is an example to prepare a design matrix for a $2^{5-2}$ fractional factorial plan:

fp_design_matrix(5) %>% 
  fp_fraction(~A*B*C*D) %>% 
  fp_fraction(~B*C*D*E)
#>  Factorial Plan Design Matrix
#>  Defining Relationship:  ~ A * B * C * D * E 
#>  Factors:  A B C D E 
#>  Levels:  -1 1 
#>  Fraction:  I=ABCD I=BCDE 
#>  Type:  plain 
#>  
#> # A tibble: 8 × 12
#>   StdOrder RunOrder .treat  .rep     A     B     C     D     E Y      ABCD  BCDE
#>      <int>    <int> <chr>  <int> <dbl> <dbl> <dbl> <dbl> <dbl> <lgl> <dbl> <dbl>
#> 1        1        9 (1)        1    -1    -1    -1    -1    -1 NA        1     1
#> 2        7       14 bc         1    -1     1     1    -1    -1 NA        1     1
#> 3       11       10 bd         1    -1     1    -1     1    -1 NA        1     1
#> 4       13       31 cd         1    -1    -1     1     1    -1 NA        1     1
#> 5       20        4 abe        1     1     1    -1    -1     1 NA        1     1
#> 6       22       13 ace        1     1    -1     1    -1     1 NA        1     1
#> 7       26       26 ade        1     1    -1    -1     1     1 NA        1     1
#> 8       32       24 abcde      1     1     1     1     1     1 NA        1     1

You can also prepare a design matrix for a $2^n$ full factorial plan, and later on augment it with a central point and then to a central composite design with axial points:

fp_design_matrix(3, rep=2) %>% 
  fp_augment_center(rep=5) %>% 
  fp_augment_axial(rep=2)
#>  Factorial Plan Design Matrix
#>  Defining Relationship:  ~ A * B * C 
#>  Factors:  A B C 
#>  Levels:  -1 1 
#>  Fraction:  NA 
#>  Type:  composite 
#>  
#> # A tibble: 45 × 8
#>    StdOrder RunOrder .treat  .rep     A     B     C Y    
#>       <int>    <int> <chr>  <int> <dbl> <dbl> <dbl> <lgl>
#>  1        1       10 (1)        1    -1    -1    -1 NA   
#>  2        2        7 a          1     1    -1    -1 NA   
#>  3        3        3 b          1    -1     1    -1 NA   
#>  4        4       16 ab         1     1     1    -1 NA   
#>  5        5        6 c          1    -1    -1     1 NA   
#>  6        6        8 ac         1     1    -1     1 NA   
#>  7        7        2 bc         1    -1     1     1 NA   
#>  8        8       13 abc        1     1     1     1 NA   
#>  9        9       12 (1)        2    -1    -1    -1 NA   
#> 10       10       11 a          2     1    -1    -1 NA   
#> # ℹ 35 more rows

Author

Paolo Bosetti, University of Trento