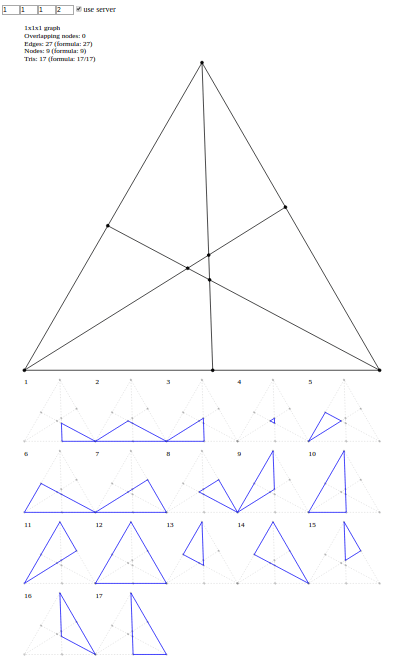
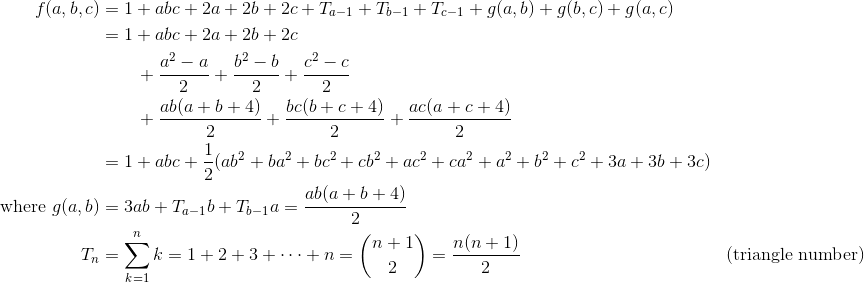How many triangles can you find?
This app proves that the number of triangles that can be made inside of an equilateral triangle where a b and c are the number of internal lines coming from the corresponding point and no 3 of those lines cross at a single point is:
It does this by generating an svg showing every possible triangle.
- If c=0, it simplifies to ½(a+1)(b+1)(a+b+2)
- If c=0 and a=b, it simplifies to (a+1)³
- When treated as a graph with a node at each line crossing and an edge between each pair of nodes in a line:
- The number of edges is a*T(b+c+1)+T(a+1)+b*T(a+c+1)+T(b+1)+c*T(a+b+1)+T(c+1)
- Where T is the Triangle Number, i.e. T(n)=n*(n+1)/2
- The number of nodes is ab + bc + ac + a + b + c + 3
- Every line from each side crosses every line from the other sides, and adds a node on the opposite base line. Plus 3 starting nodes from the base triangle.
- If c=0, the number of triangles is edges-nodes+1
- The number of edges is a*T(b+c+1)+T(a+1)+b*T(a+c+1)+T(b+1)+c*T(a+b+1)+T(c+1)
lein run and visit localhost:3000
The four boxes are a, b, c, and o, where o is an offset to add to each angle to prevent 3 lines from crossing a single point.
To the extent possible under law, the person who associated CC0 with this work has waived all copyright and related or neighboring rights to this work.