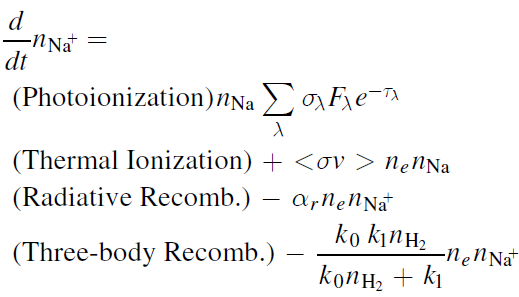IMAGE: European Southern Observatory
Exoplanets orbiting close to their host star are expected to support a large ionosphere, which extends to larger pressures than witnessed in our solar system. These ionospheres can be investigated with ground-based observations of the optical signatures of alkali metals, which are the source of the ions. Alkali metals produce prominent features in optical transit spectra of exoplanets, e.g. the Na and K doublets at 589.3 and 766.4 nm, respectively. These metals readily ionize in the hot atmospheres of close-in exoplanets and are predicted to produce an extensive ionosphere more like that of a star, rather than Jupiter. Measurements of alkali densities are essential to understand the structures of the spectroscopically observable exoplanets as the ions affect the temperature structure and circulation (through ohmic dissipation and ion drag).
- Python 3
- Matplotlib
- Numpy
- Scipy
This repo can help calculate the alkali abundances in exoplanetary atmospheres subject to ionizing radiation. See XO2b_Na_profile.py for an example of how to balance the equation:
in each layer of a 1D atmosphere to derive the Na mixing ratio profile as a function of pressure (Pearson et al. 2019 ). An example output looks something like this:
Please cite the following article if you make use of this code in anyway and hit that star button
Ground-based Spectroscopy of the Exoplanet XO-2b using a Systematic Wavelength Calibartion
@article{1538-3881-157-1-21,
author={Kyle A. Pearson and Caitlin A. Griffith and Robert T. Zellem and Tommi T. Koskinen and Gael M. Roudier},
title={Ground-based Spectroscopy of the Exoplanet XO-2b Using a Systematic Wavelength Calibration},
journal={The Astronomical Journal},
volume={157},
number={1},
pages={21},
url={http://stacks.iop.org/1538-3881/157/i=1/a=21},
year={2019},
}
Radiative recombintion, thermal ionization and 3-body recombination can be easily calculated using the ion() class in Ionization.py. Photoionization is also supported but requires some additional parameters regarding the exoplanet's atmosphere (See XO2b_Na_profile.py). An example of how to compute certain rate coefficients:
from Ionization import ion, NaI
if __name__ == "__main__":
# some basic functions
density = lambda P, T : (P*1e6) / (kb*T) # pressure in bars -> barye (cgs)
ev2nm = lambda e: 1239.84193/e
nm2ev = lambda n: 1239.84193/n
# able to call a function both ways
#ewaves = nm2ev( np.linspace(5,121,40) )
#cross = ion.ionization_crosssection( ewaves, HI)
#cross = ion.ionization_crosssection( ewaves, 4.298e-1,5.475e4,3.288e1,2.963,0,0,0)
# define our atmospheric parameters
T, P = 1500, 10 # [K], [bar]
ni = 1e-10 # Na ion mixing ratio (same as electron mr)
nna = 3e-6 - ni # neutral Na mixing ratio
# function will automatically get coefficients from ion.NaI dictionary
thermal_rate = ion.ionization_thermal(T, NaI) # cm^3 / s
# rate coefficient * neutral Na density * electron density
thermal_ionization = thermal_rate * (nna*density(P,T)) * (ni*density(P,T))
# compute radiative recombination rate
recom_rate = ion.recombination_radiative(T, NaI)
# assume ion density = electron density
radiative_recombination = recom_rate * (ni*density(P,T))**2
print("thermal rate coefficient <ov> [cm^3 s^-1] {:.2e}".format(thermal_rate))
print("thermal ionization production [s^-1 cm^-3] {:.2e}\n".format(thermal_ionization) )
print("rad recombination rate coeff [cm^3 s^-1] {:.2e}".format(recom_rate))
print("radiative recombination prod [s^-1 cm^-3] {:.2e}".format(radiative_recombination) )For additional support see the main block of code in Ionization.py
This code currently supports Na. Additional atoms must be added in separately using the same format as the dictionaries for atoms (See line ~27 in Ionization.py). Coefficients for each dictionary can be found here
- Radiative recombination rates - Verner 1996a
- Photoionization cross sections - Verner 1996b
- Ionization rate coefficients of atoms by electron impact - Voronov 1997
- 3 body recombination -
- support for additional ions (e.g. K, Li, H)