TRABALHO PRÁTICO 1 – Estimativa de Preços de Imóveis (problema de regressão)

Informações

Curso: EEL860 – Tópicos Especiais em Sistemas de Controle (2018/1)

Aluno: Pedro Santos Eusébio

DRE: 1130133851

Período: 11

repositório: https://github.com/pedroeusebio/machine-learning

Introdução

A proposta deste relatório é apresentar todo o caminho e desenvolvimento que foi necessário para analisar o dataset House Prices: Advanced Regression Techniques.

Análise

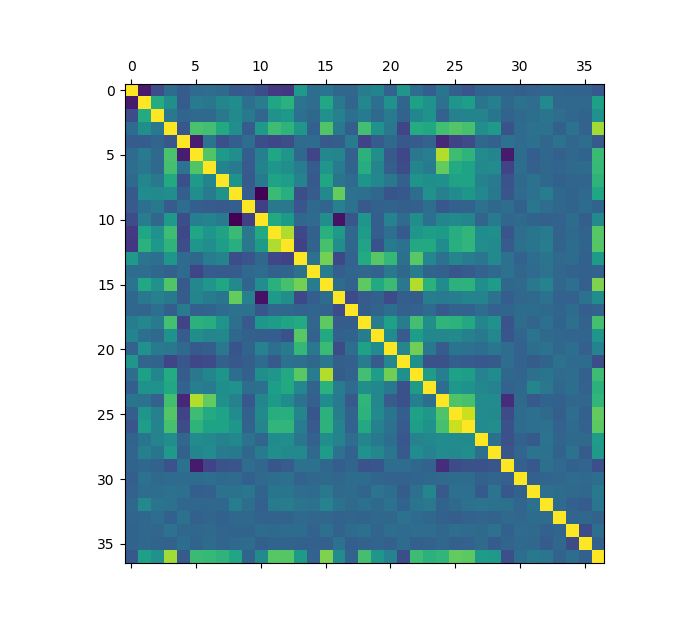
Para a análise desse dataset foi necessário avaliação de cada feature com o objetivo de entender o conteúdo de cada caracteristia das csas e poder prever melhor o comportamento. Inicialmente, foi feito a análise utilizando a matriz de correlação, o objetivo é entender a relação de cada feature ao ponto de descartar as que era mais correlacionadas para não enviesar o modelo. A imagem a seguir ilustra a matriz de correlação:

Analisando a matriz de correlação percebemos que temos algumas características fortemente correlacionadas. Entre elas:

GarageYrBlt e YearBuilt - ambos representam datas de construção da garagem e o apartamento, respectivamente.
1stFlrSF e TotalBsmtSF - representa a correlação entre a área do primeiro piso e a área total do porão.
TotRmsAbvGrd e GrLivArea - representa a correlação entre a quantidade de quartos de ouros andarea e a área acima do solo.
GaregeArea e GaregeCars - representa a correlação entre a área da garagem e a quantidade de carros que cabem na garagem.

Além disso, foi analisado os dados de cada coluna com o objetivo de entender quais que poderiam possuir valores vazios (NA), quais que possuiam valores numéricos e quais que deveria ser subistituidos por valores numéricos discretos ou continuos. Para isso foi utilizado a função abaixo:

def analising_missing_values(dataset):
    analise = {}
    for col in xrange(len(dataset)-1):
        possible_values = set(dataset[col])
        analise[col] = {'possible_values': len(possible_values), 'na_percent': Decimal(0)}
        if 'NA' in list(possible_values):
            analise[col]['na_percent'] = Decimal(dataset[col].count('NA')) / Decimal(len(dataset[col]))
    return analise

Essa função faz a análise de cada coluna, vendo quais são os possiveis valores e a quantidade de valores faltantes (NA). Retorna um dicionário que contém a porcentagem de valores faltantes e quantidade de possiveis valores.

Foi gerado também a matriz de dispersão das features mais correlacionadas com o preço de venda dos imóveis:

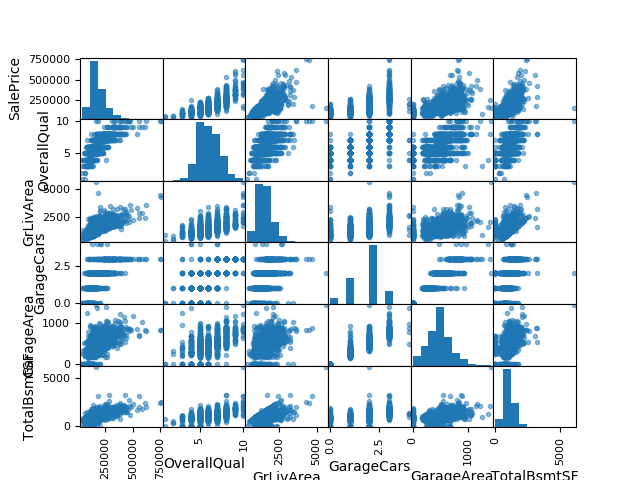
Essa matriz pode ser usada para ver a disperão simultânea de cada caracteristica simultaneamente ao ponto de verificar como as distribuições são correlacionadas.

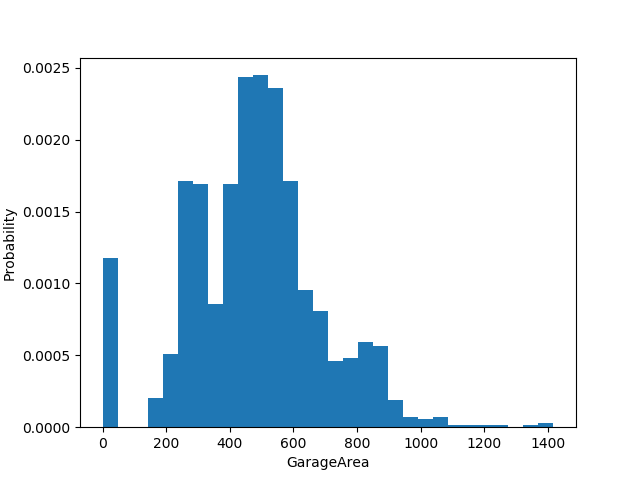
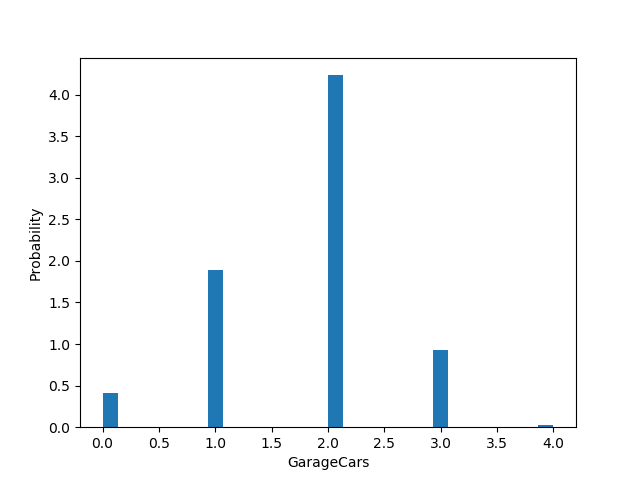
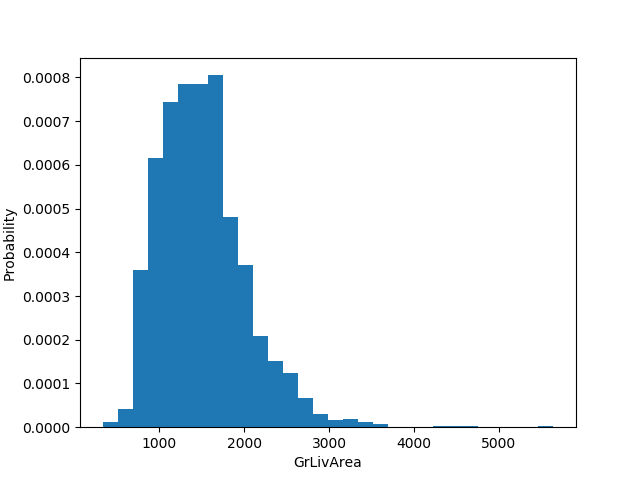
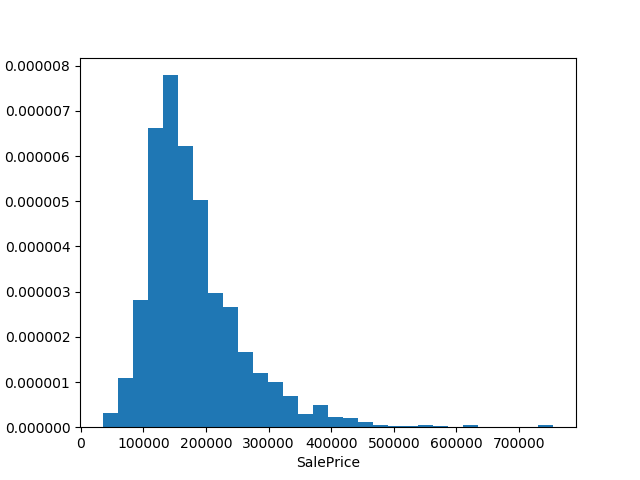
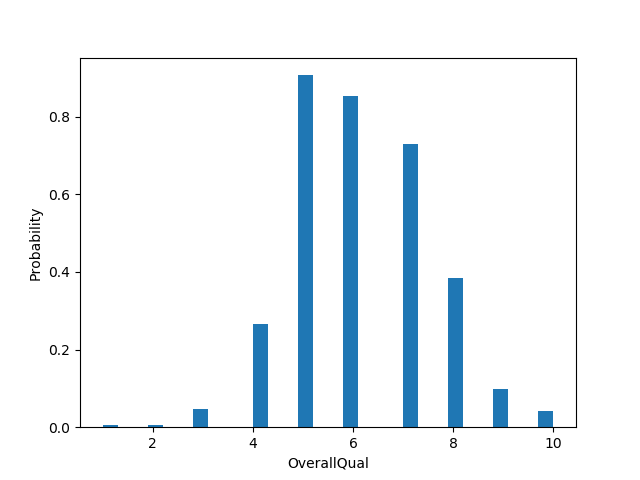
Também foram gerados distribuições das features mais correlacionadas com o preço de venda das casas, podendo assim ver de maneira mais detalhada cada uma delas. Podemos perceber, no geral, que elas a distribuíção respeita a distribuição normal:

Preparação dos dados

Para a preparação dos dados foram utilizados três técnicas: Hashing trick, o preenchimento de dados vazios e a normalização dos dados.

Utilizando a função analising_missing_values podemos perceber um padrão e avaliar os parâmetros que seriam utilizados na função de hashing_trick.

A quantidade de possíveis valores para cada coluna foi utilizado na aplicação da técnica de Hashing Trick. Essa técnica é usada para trocar os valores de texto para valores numéricos sem alterar a correlação entre eles. Dado uma coluna, cria-se uma coluna nova para cada possibilidade existente, e paaa cada linha que possuia um daqueles valores, é trocada de 0 para 1 na coluna que presenta essa característica. Dessa forma, não cria uma relação de grandeza entre as características, o que ocorreria se trocassemos os valores de texto por númeoros ordenados. Dessa forma, o dataset antigo de 80 colunas de features passou a ter 520 colunas, e esse novo dataset gerado foi utilizado nos métodos de regressão.

O código abaixo representa a função de hashing trick:

def hashing_trick(train_dataset, test_dataset, unique_values=20, cols_to_remove=[]):
    new_header = create_column(train_dataset)
    hashing_trick_columns = []
    for col in xrange(1,len(train_dataset) - 1):
        if len(set(train_dataset[col])) <= unique_values and col not in cols_to_remove:
            hashing_trick_columns.append(new_header[col])

    training_lines = len(train_dataset[0])
    test_lines = len(test_dataset[0])

    merged_dataset = np.concatenate((train_dataset[:-1], test_dataset), axis=1)

    data_frame = pd.DataFrame(data=np.transpose(merged_dataset), columns=new_header[:-1])

    for col in hashing_trick_columns:
        dummies = pd.get_dummies(data_frame[col])
        data_frame = pd.concat([data_frame, dummies], axis=1)
        data_frame.drop([col], inplace=True, axis=1)

    train_data_frame = pd.concat([data_frame[0:training_lines],
                                  pd.DataFrame(train_dataset[-1], columns=['salesPrice'])], axis=1)
    test_data_frame = data_frame[training_lines:]

    print(len(train_data_frame.columns))
    print(len(test_data_frame.columns))

    train_data_frame.to_csv('dataset/processed/trainWithHashTrick.csv', index = False, header=False)
    test_data_frame.to_csv('dataset/processed/testWithHashTrick.csv', index = False, header=False)

De maneira simples, a função avalia as possibilidades de cada coluna e caso seja menor que o parâmetro, essas colunas são trocas por dummies. No final, esse novo dataset é salvado em arquivo para que não seja necessário a rerodução do método para o desenvolvimento da regressão.

Além disso, foi utilizado a média de cada coluna para preencher os valores que eram faltantes, tomando o devido cuidado com as colunas que possuiam a possibilidade de dados faltantes representarem alguma informação relevante, como o caso 2ndFlrSF e Condition2 que poderiam ou não existirem. o Código abaixo representa a implementação dessa técnica:

filled_train_df = train_df.fillna(train_df.mean())

E por fim, foi realizado a normalização de cada coluna de feature dos dados, como aponta o código abaixo:

min_max_scaler = preprocessing.MinMaxScaler()
x_saled = min_max_scaler.fit_transform(x)
filled_train_df = pd.DataFrame(x_scaled)

Algoritmos de Regressão e Treinamento

Para a avaliação desse trabalho foram usados diversos algoritmos de regressão com o objetivo de encontrar um modelo que consiga diminuir o erro em relação ao resultado calculado e o real. Entre eles temos : Regressão Linear, Ridge, Lasso, Lars, Orthogonal Matching Pursuit, Bayesian Ridge, Gradient Boost, Random Forest e por fim Ada Boost.

Para cada modelo utilizado, foram usados a técnica de falidação cruzada e e Kfold. Ambas as técnicas são usadas para melhorar o desempenho do treinamento e dessa forma promover melhores resultados. O código abaixo ilustra como as técniacs foram utilizadas:

def fit_models(features, target, test_df, num_folds, test_size=.2, save=False):
    results = {}
    for i, model in enumerate(get_regression_models()):
        m = model[1]
        kfold = KFold(n_splits=num_folds)
        result = cross_val_score(m, features, target, cv=kfold)
        m.fit(features, target)
        predicted = m.predict(test_df)
        pred_df = pd.DataFrame(np.transpose(predicted), columns=['SalePrice'])\
                    .rename(index={x: x + 1461 for x in range(len(predicted))})
        pred_df.index.name = 'Id'
        if save:
            pred_df.to_csv('dataset/prediction/predict{}.csv'.format(model[0]), header=True)
        results[model[0]] = {
            'score': result.copy(),
            'score_mean': np.mean(result),
            'predict': pred_df.copy()
        }
    return results

O Kfold, utilizado acima, retorna os índices dos itens que usados para teste e treino fazendo assim uma seleção e mistura dos dados. Como paramêtro foi passado somente a quantidade de combinações dos dados para teste e treino. Esses folds foram usados na função cross_val_score que utiliza a técnica de validação cruzada e retorna uma nota que representa a avaliação da validação cruzada. Como o parâmetro dessa função foram passados o modelo, as features tratadas como descrito acima, target que representa a coluna de SalePrice do dataset de treinamento e por fim os índices que serão usados para treinamento e teste. A variável 'result' recebe uma lista com 10 avaliações que foram feitas para cada fold que foram usadas como base para a decisão do melhor modelo para o dataset.

tabela de resultados

A tabela de resultados abaixo é a avaliação de cada modelo para cada fold realizado pelo metodo cross_val_score Podemos perceber que entre eles, tivemos um desempenho melhor dos modelos de Gradient Boost, Random Forest e Bayesian Ridge, com um destaque maior para o primeiro que teve uma média de avaliação de 0.8770437653896043.

Fold	1	2	3	4	5
AB	0.78506898	0.81426123	0.81454807	0.64364507	0.81458887
LA	-1.08158543e+73	-1.77269963e+52	-9.57560286e+37	-4.53991633e+14	-3.10037499e+39
Lo	0.87192173	0.90969565	0.89872808	0.72510226	0.89084769
RF	0.86697293	0.85274094	0.84643701	0.67719027	0.84540046
LR	0.86723811	0.88801362	0.91278184	0.72440244	0.89142096
GB	0.89075798	0.88941048	0.8633984	0.74449904	0.89715311
BR	0.89748324	0.90737767	0.8776898	0.75672072	0.89329666
R	0.88979644	0.91288842	0.89600697	0.74449146	0.89085991
OMP	0.89124489	0.92423339	0.93404012	0.71609474	0.91132478

Fold	6	7	8	9	10
AB	0.82145989	0.79623606	0.73910663	0.7784952	0.76311893
LA	-3.58806819e+36	-8.51106846e+67	-2.30675821e+54	-5.75285594e+48	-1.29257427e+51
Lo	0.642747	0.86642567	0.88962677	0.48865479	0.85208643
RF	0.88283748	0.86834124	0.87146545	0.76239102	0.85933532
LR	0.64079842	0.86464072	0.88933797	0.40409366	0.79675697
GB	0.88414065	0.89379331	0.93757344	0.87855912	0.89115213
BR	0.8833572	0.87706995	0.88616824	0.5767759	0.88942955
R	0.83364692	0.89085991	0.88795322	0.51532244	0.8648772
OMP	0.68125843	0.88698	0.90876031	0.56701896	0.88000898

Dessa maneira, o Gradient Boost foi escolhido como modelo principal e por conta disso, foram feitos diversos testes mudando os parâmetros do modelo até encontra um que melhorasse ainda mais o desempenho do modelo. os parâmetros passados foram:

ensemble.GradientBoostingRegressor(alpha=0.9, criterion='friedman_mse', init=None, learning_rate=0.1,
                                   loss='ls', max_depth=5, max_features=None, min_samples_leaf=1,
                                   min_samples_split=2, min_weight_fraction_leaf=.0, n_estimators=400,
                                   presort='auto', random_state=None, subsample=1.0, verbose=0,
                                   warm_start=False)

Com esses parâmetros foi possível melhorar significativamente a posição no Kaggle, saindo de 4083, como o modelo simples de Regressão Linear, para 2358 com o Gradient Boost. Todos as predições geradas foram salvos em um arquivo csv e estão no repositório do projeto.