This is the code of my final mini-project presented for the online course "Machine Learning for Physicists 2020" offered by the University of Erlangen-Nuremberg and lectured by Florian Marquardt during the COVID-19 lockdown.
A Gaussian-Bernoulli Restricted Boltzmann Machine is trained to learn and reproduce the statistics of a set of 100 quantum mechanical harmonic oscillators at thermal equilibrium and fixed frequency. Thermodynamic quantities are computed as ensemble averages from the generated samples and compared to the theoretical values as a means of validation.
The neural network is fed with 300,000 samples of sets of these oscillators (generated with a Monte Carlo approach) as a Gaussian layer. The quantum numbers that define the state of the oscillators are normalized to 1 considering that, given the conditions arbitrarily set for the temperature and frequency, capping the generator to a maximum quantum number of n_max=10 is enough to capture the physics of these ensembles.
To install and train the neural network, run:
$ pip install -r requirements.txt
$ cd miniproject
$ python train.py
For a more detailed description, you can refer to the report I wrote for the course. A very brief presentation is also available.
The neural network was defined according to the guidelines described in Geoffrey Hinton's "A Practical Guide to Training Restricted Boltzmann Machines (Version 1)" and the set of hyper-parameters chosen is:
- amount of hidden units = 70
- batchsize = 10
- learning rate = 0.005
- no momentum, weight-decay nor sparse targets
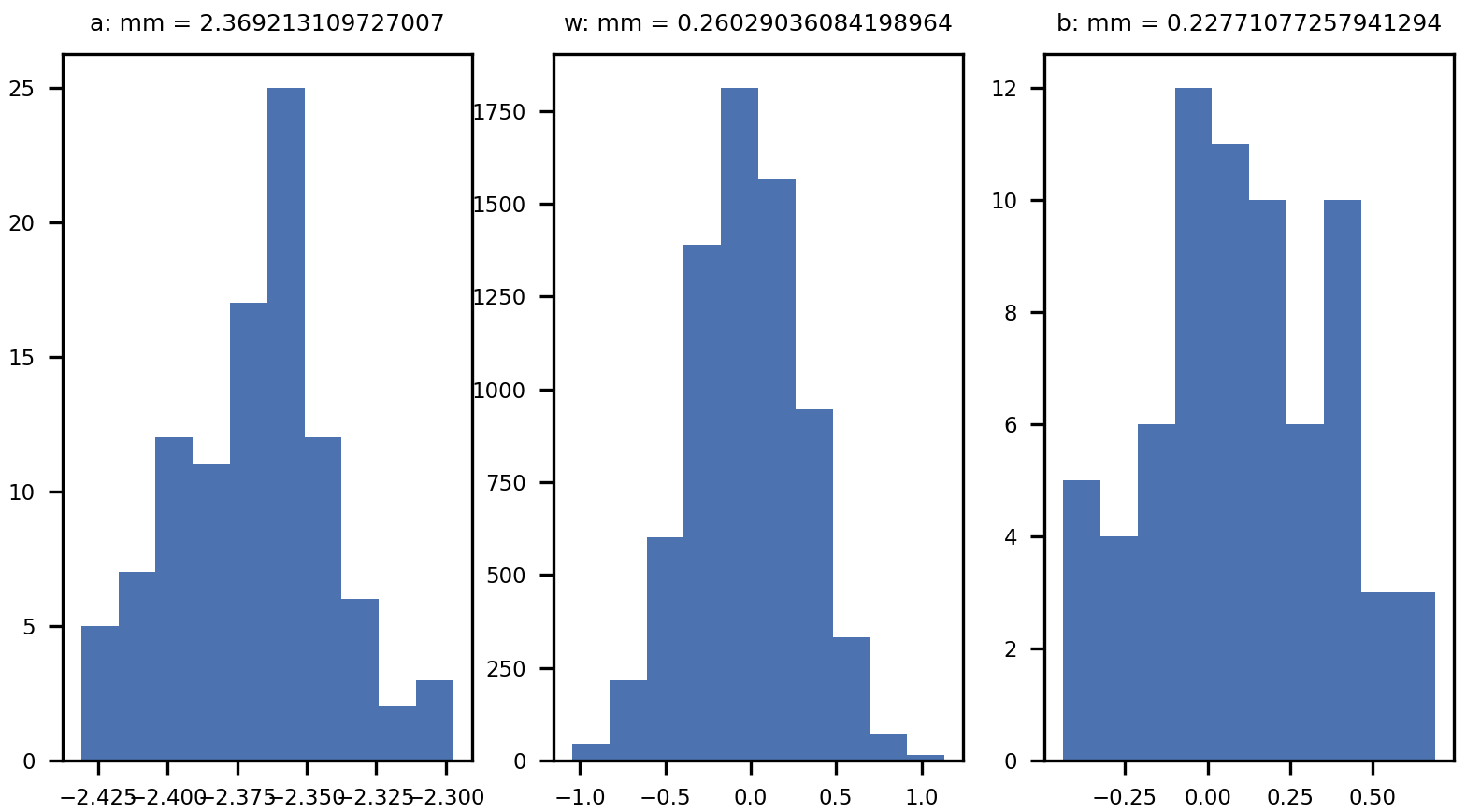
After 300,000 training steps using contrastive divergence, the final state of the neural network (which can be found at /miniproject/data/) can be pictured with the histogram of weights and biases:
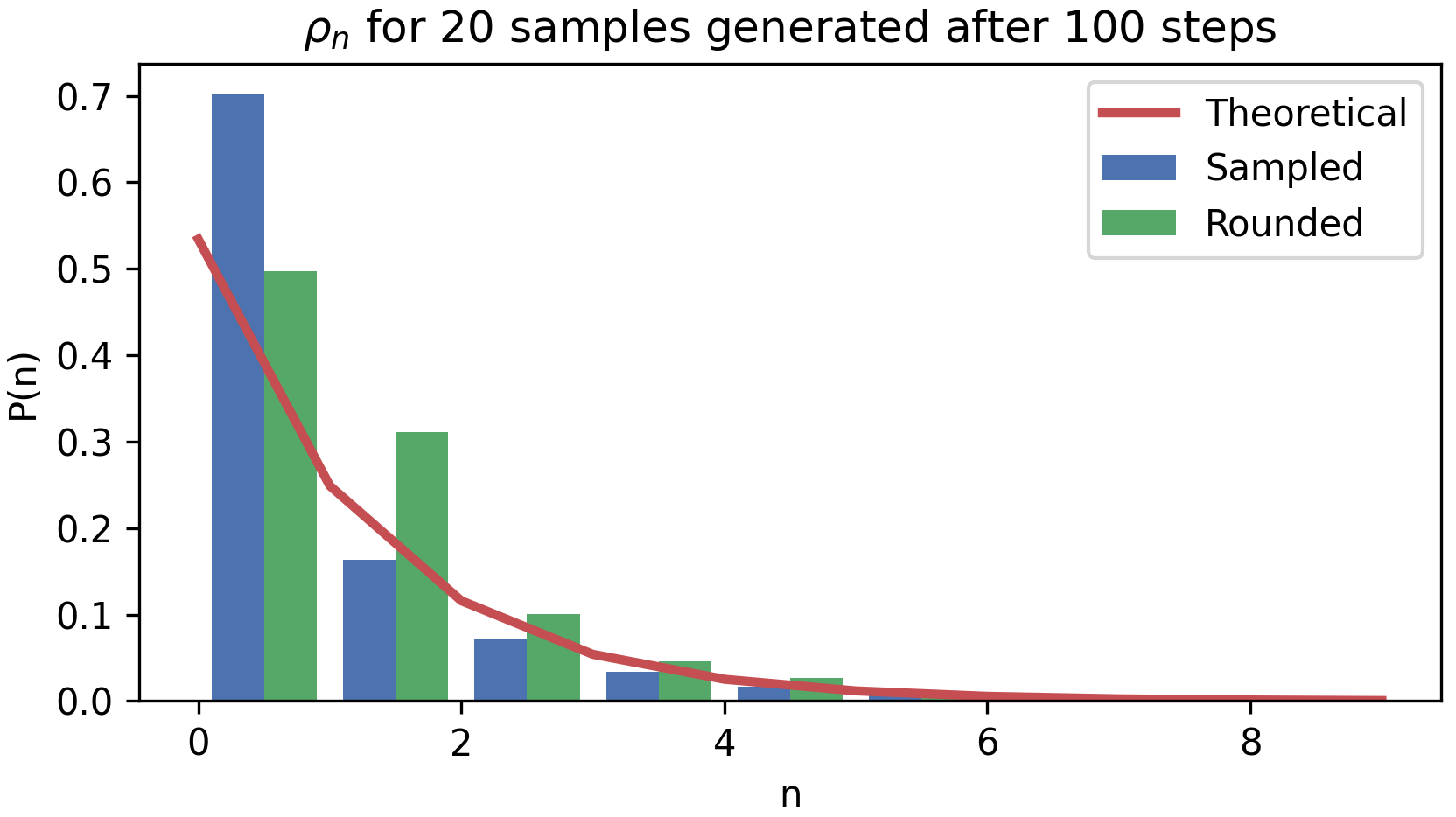
And the generated probability distribution, along with the thermodynamic quantities calculated from the generated samples (in the SI), are:
| Theoretical | Sampled | Rounded | |
|---|---|---|---|
| < E > | 1.4471307636e-26 | 1.441212123e-26 | 1.3788526515e-26 |
| <\epsilon_n> | 1.4471307636e-28 | 1.4412121231e-28 | 1.3788526515e-28 |
| < n > | 0.872244867016 | 0.866632503412 | 0.8075 |
Where two approaches are considered:
- Taking the
Sampledquantum numbers generated by the Gaussian layer of the RBM. These can take any value from 0 to 1. - Denormalizing these sampled values and considering the
Roundedvalues of these quantum numbers (to the closest integer) to get a "more physical result".
Which can be reproduced by running:
$ cd miniproject
$ python results.py
Licensed under the MIT License.