提示:如果你无法渲染其中的公式,请阅读 README.pdf,二者内容相同。
探索晶体材料的新奇电子结构是凝聚态物理学的重要课题之一。
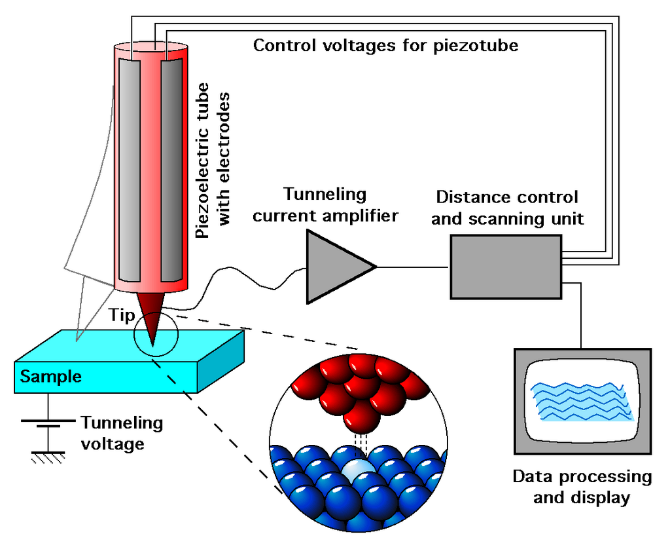
扫描隧道显微学(Scanning tunneling microscopy, STM)与隧道谱学(Scanning tunneling spectroscopy, STS)能够直接测量材料表面原子晶格结构与能态密度(Density of states, DOS)。该测量方法对于探究材料表面态(Surface state)或石墨烯等层状材料的准二维电子结构则更加具有优势。
扫描隧道显微镜利用量子隧穿效应,对探针和表面之间的隧穿电流大小的探测,可以观察表面上单原子级别的起伏。
通常认为扫描隧道显微镜(Scanning tunneling microscope, STM)探测到的都是实空间(Real-space)的信号,要想得到倒空间(k-space)的信息还得依赖于其它具有动量分辨能力的测量手段。例如,角分辨光电子谱(Angle-resolved Photoemission Spectroscopy , ARPES)是一种能直接获得电子动量与能量的测量方法。
那么,我们有没有可能同时获得实空间与动量空间的信息呢?或者说,我们有没有可能从实空间的图像中找出动量空间的信息呢?
我们知道实空间与动量空间之间存在傅里叶变换的关系,因此可以尝试使用傅里叶变换的手段从STM 测到的实空间图像中获得动量空间的信息,进而对能带结构进行进一步深入的研究。这类方法被称作傅里叶变换隧道谱学(Fourier Transform STS, FT-STS)的方法,
那么 FT-STS 的基本原理是怎样的呢?我们通过 STM 测量样品在某个能量上各处的局域能态密度(Local DOS)。当样品上有杂质时(真实材料中往往如此),该处的波函数将被散射。由于该散射过程通常是相干的,入射波与反射波将相干叠加形成驻波,对局域能态密度形成调制,所形成的波纹状图案通常被称为准粒子干涉(Quasiparticle Interference, QPI)图样。
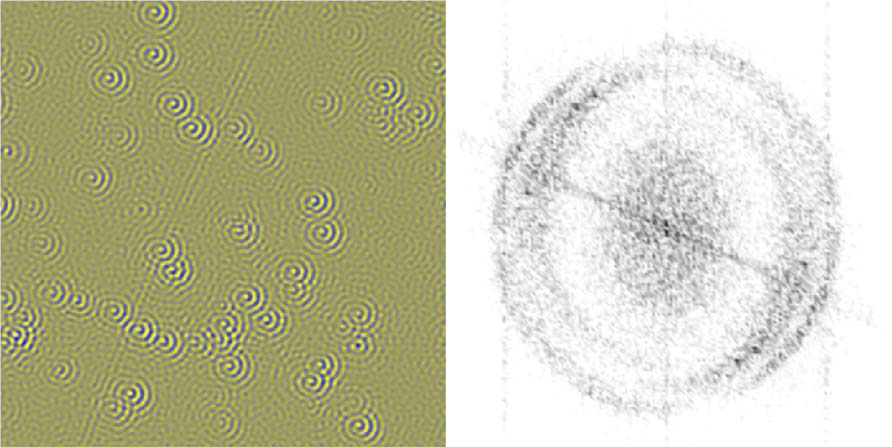
铜表面二维电子气的 QPI 图样及其 FFT [Nat. Commun. 6, 8691 (2015)]
利用对 QPI 分析,人们研究了石墨烯(Graphene)[Science 317, 219–222 (2007)],铜氧化物高温超导体(High-Tc Cuprate Superconductors)[Science 297, 1148–1151 (2002)]、铁基超导体(Fe-based Superconductors)[Nat. Commun. 7, 10565 (2016)]等新奇材料的电子结构,极大促进了人类对物质世界的认识与理解。
布洛赫定理告诉我们, 周期性势场作用下,薛定谔方程的解将呈现布洛赫波的形式 $$ \psi(\vec{r})=e^{i \vec{k} \cdot \vec{r}} u(\vec{r}) $$ 其中 $ u(\vec{r}) $ 是周期函数,满足 $ u(\vec{r})=u\left(\vec{r}+\overrightarrow{R_{n}}\right) $
由于周期性势场中的布洛赫波具有周期函数的性质,我们可以用类似于时域中的周期信号的处理方法,对实空间做二维傅里叶变换,得到k空间。具体而言,k空间是一个以傅里叶变换后得到的倒格矢为基矢的离散的格点空间。粒子在倒空间上的某点上意味着它处于某一能量本征态,进而每一点都有确定的能量测量值。
由诺特定理,每一种连续对称性对应一个守恒量。由于真空有空间不变性,这导致了真空中的动量守恒。然而,固体中晶格的出现打破了一部分空间不变性,把连续对称变成了有限周期对称。这时,粒子动量在周期场调制下不再守恒,但仍然有一个东西“准守恒”,那就是准动量。
类比对一维粒子位形空间的波函数进行傅里叶变换时,选择的基函数是 $ \exp (ikx) $,动量本征态,这里的k就代表动量。
在有晶格周期的固体物理中进行傅里叶变换时,选择的基函数是 $ \exp (ikx) u_k(x) $,这里的k不再是严格意义上的动量,称为准动量。
等能面: 晶体中电子的准经典运动主要取决于E-k关系,为了表示实际晶体的复杂的能带结构,常常使用等能面来反映E-k关系,所谓等能面是指由k空间的能量相同的各点构成的曲面。
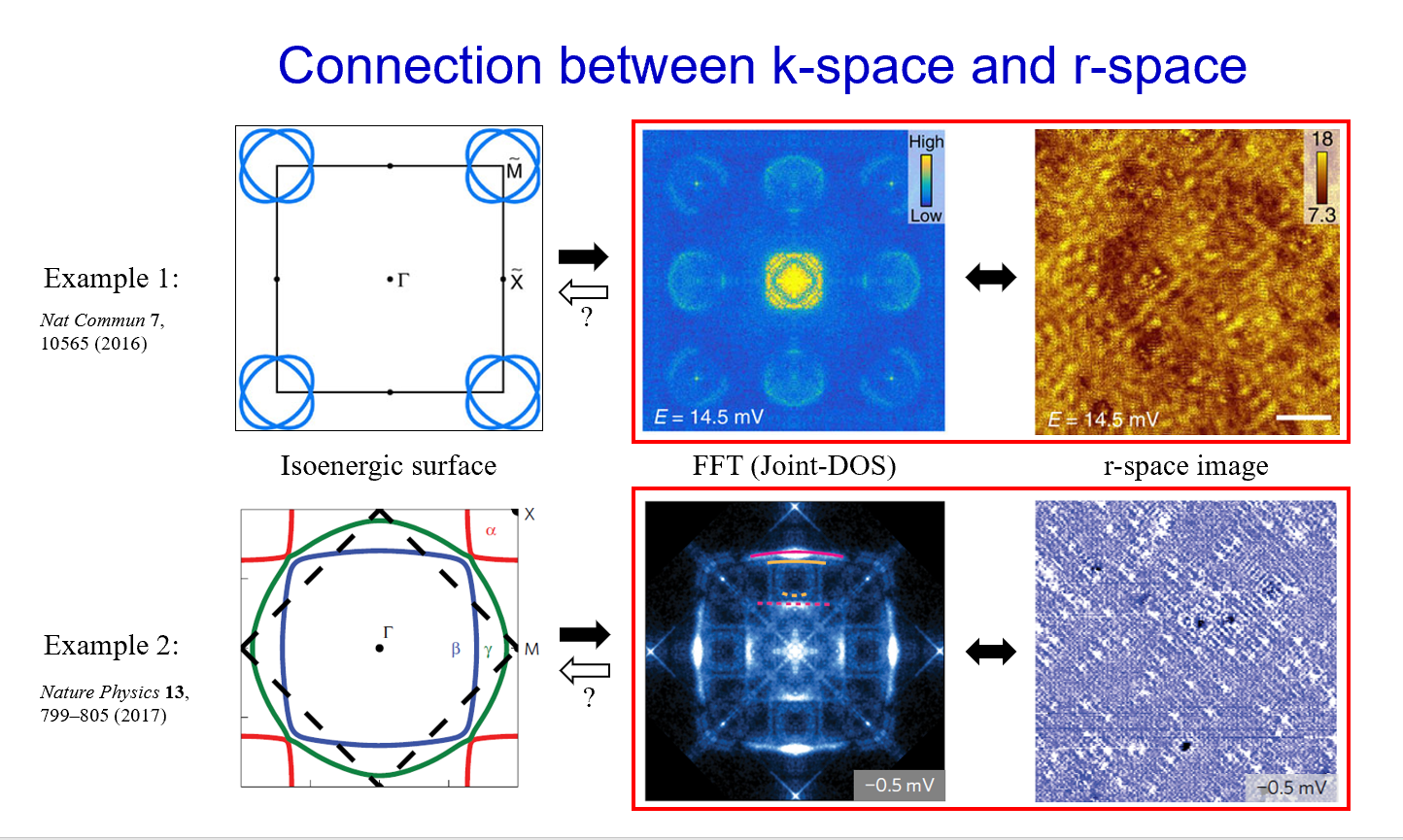
在示意图中我们可以看到:
- 第三列为扫描电镜得到的真实实验结果(实空间)
- 第二列为真实实验结果经过二维傅里叶变换FFT之后的图像
- 第一列为我们的目标:干净的等能面结构
总结上面提到的固体物理背景,动量空间中的信息通过散射过程投射到了实空间的数据中。因此,通过对实空间图像进行傅里叶变换,我们将能得到驻波的波矢信息,进而推断出等能面(Isoenergic Surface)的结构。
本大作业旨在同学们掌握通过局域态密度图(Local DOS Map)得到二维等能面结构(Isoenergic Surface)的基本原理与相关数据处理方法。
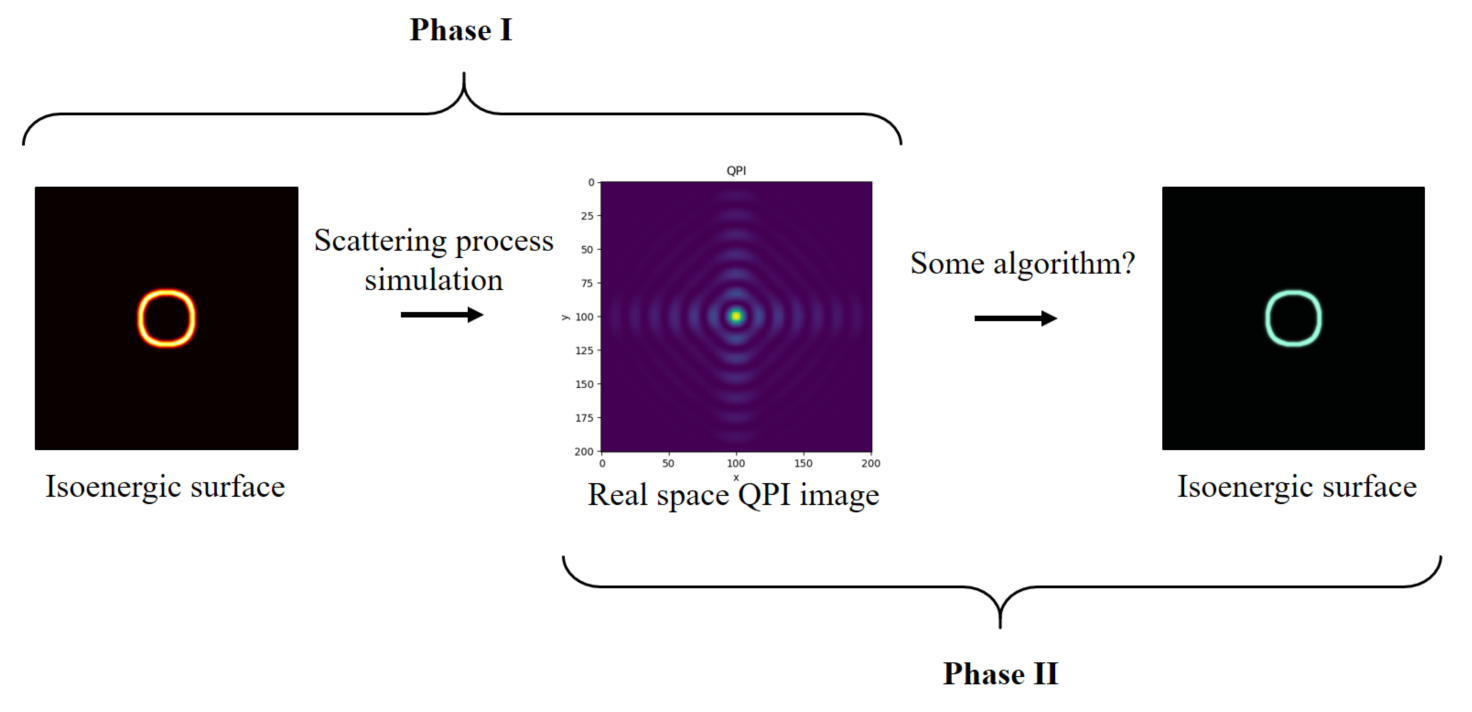
由于作业的评分一致性要求,我们不采用真实QPI数据上的结果作为评分依据,而以模拟的方式进行两个阶段的模拟任务:
- 大作业第一阶段(simulation):即利用假设的动量空间等能面结构,生成中心散射点(两种不同类型的杂质)附近区域的局域态密度图,即 QPI 图样。
- 这一阶段的目的是让大家熟悉物理背景,了解数据的格式,通过模拟知道QPI数据理论上的生成机制
- 大作业第二阶段(data mining):第一阶段的逆过程,即通过给定的QPI 图样数据反推动量空间等能面结构。
- 这一阶段的目标是真正从(模拟的)QPI图样数据中找到等能面结构,以给定的模拟数据作为评分标准,如果结果较好可以进一步在真实的QPI实验数据中应用。
100 份不同的等能面附近的态密度分布,存在 dos-momentum 中。每份数据是一个 HDF5 文件,文件中 /isoE 是一个 (201, 201) 的二维数组,数字代表电子在倒空间中的态密度。其中倒空间的单位为任意值,态密度的归一常数也是任意值:在本问题中,只有相对强度有明确的物理意义。
dos-position 代表普通散射中心的实空间,dos-position/m 代表磁性散射中心的实空间,dos-position/damp 代表衰减的普通散射中心的实空间,dos-position/m/damp 代表衰减的磁性散射中心的实空间。
将以上的路径中 dos-position 替换成 STM,则对应相应输出数据的可视化图。
输入数据的可视化图在 p_momentum 目录中。
本次作业提供了 Makefile,最终助教也将使用 Makefile 进行测试。需要注意,你在编写所有程序文件时,都应该使用 make 给程序传入的参数(来自 sys.argv),而非硬编码下面提到的任何文件名或文件编号等信息;否则,你可能无法通过测试。
在本目录中运行 make -n 即可看到实际运行的命令,这或许能帮助你开发。
作业基础要求分成以下几个部分,完成各个任务即可拿到相应分数。
| 任务(程序名) | 功能 | 分数 |
|---|---|---|
| scatter.py | 从动量空间生成实空间 | 40 |
| gimage.py | 实空间/倒空间可视化 | 20 |
| damping.py | 生成考虑距离衰减的实空间 | 12 |
| multi_scatter.py | 生成多散射点叠加的实空间 | 8 |
以下是三个文件具体的输入输出格式要求。
读取 dos-momentum/%.h5,输出 dos-position/%.h5,其中%代表从 0000 到 0099 的字符串。以 dos-momentum/0023.h5 程序的调用形式形如:
python3 scatter.py 0 dos-momentum/0023.h5 dos-position/0023.h5其中第一个参数 0 代表普通散射中心模式,即入射波和出射波在散射中心没有相位差。如果第一个参数是 1,代表磁性散射中心模式,即入射波和出射波在散射中心有
设倒空间(k空间)的态密度为
如果散射中心有磁性,即 sys.argv[1] 为 1 时,需要给出射波填加一个
读取实空间(当 sys.argv[1] 为1)或倒空间(当sys.argv[1] 为 0)的二维态密度数组,画出可以表征二维标量场的图形。以 dos-momentum/0023.h5 为例,程序的调用形式形如:
python3 gimage.py 0 dos-momentum/0023.h5 p_momentum/0023.png注意标注横纵坐标的标签、图的标题。
提示:备选之一为 matplotlib.pyplot.imshow。
对理想条件下的散射态密度依距离衰减:
其中
python3 damping.py dos-position/0058.h5 dos-position/damp/0023.h5dos-position 各级目录下的 .h5 文件中,都使用名为 /QPI 的 (201,201) 二维数组来存储实空间的 QPI 图样。
注意本题仅需要生成一张图片
在实空间进行平移,使生成散射点不在图像中心,并生成存在多个散射点叠加干涉的 QPI 图样。在本题中我们仅仅要求考虑一阶散射及其衰减,不考虑二阶及以上,或者复杂路径的散射情况,态密度为每个散射点折返路径引发相位和原始相位的叠加。以位于
$$ D(\mathbf{r}) = \left| 1 + \int \int \mathrm{d}\mathbf{k}_1 \mathrm{d}\mathbf{k}'_1 f(\mathbf{k}_1) f(\mathbf{k}'_1) e^{-i (\mathbf{k}_1 - \mathbf{k}'_1)(\mathbf{r}_1 - \mathbf{r})} e^{-\frac{2|\mathbf{r}_1 - \mathbf{r}|}{L}} + \int \int \mathrm{d}\mathbf{k}_2 \mathrm{d}\mathbf{k}'_2 f(\mathbf{k}_2) f(\mathbf{k}'_2) e^{-i (\mathbf{k}_2 - \mathbf{k}'_2)(\mathbf{r}_2 - \mathbf{r})} e^{-\frac{2|\mathbf{r}_2 - \mathbf{r}|}{L}} \right |^2 \ $$ 更多的散射点依此类推。
生成QPI实空间图样保存路径为dos-multi-position,散射中心坐标存储在multi_scatter_position.csv
本题中选择叠加的等能面序号为:01
程序的调用形式为:
python3 multi_scatter.py 0 multi_scatter_position.csv dos-momentum/0001.h5 dos-multi-position/0001.h5提高要求为加分项,至多可加 10 分。
可以参考的提高要求选题:
- 为不同散射过程指定不同散射概率。即对于一组
$(\mathbf{k}_1,\mathbf{k}_2)$ ,其发生概率P依赖于$\mathbf{k}_1$ 和$\mathbf{k}_2$ 。而在基本要求中,我们认为不同散射过程是等概率的。可以采用的形式如:
或者用矩阵形式进行任意指定。
-
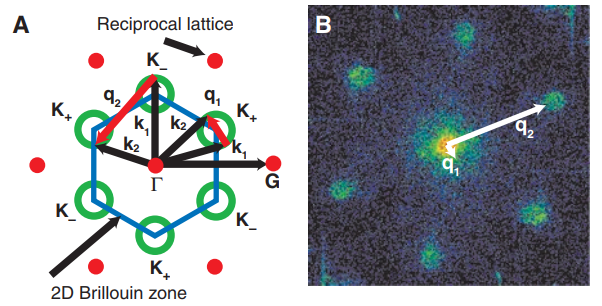
生成二维石墨烯的QPI图像
参考文献:Rutter, G. M., Crain, J. N., Guisinger, N. P., Li, T., First, P. N., & Stroscio, J. A. (2007). Scattering and interference in epitaxial graphene. Science, 317(5835), 219-222.
如果你实现了任何提高要求,请在实验报告中详细说明你的工作,这将作为评分的依据。
非功能部分的要求详见大作业公告,此部分占20分。