Memorably, computer science — the subject matter of the book — is presented as a non-science whose signficance has little to do with computers (see also the lecture). Just as memorably, computer science is presented as a branch of epistemology, that is, the study of knowledge (which, tipically, is considered part of philosophy). In particular, computer science is procedural epistemology. We deal here with the systematization of imperative, how-to, knowledge, as opposed to “declarative” knowledge. The computer scientist deals, indeed, with a complexity that resembles that of the human mind — notice the epigraph from Locke. Much of his job is dominating the “intellectual complexity” of software systems.
Here is a bullet-point summary up to section 1.1 (included) and my solutions of the exercises. As expected these first pages present fundamental concepts and building blocks.
- The subject matter of this book involves three foci of phenomena
- the human mind;
- collection of computer programs;
- the computer.
- Idioms: “standard program structures of whose corrected we have becamse sure”.
- Algorithms: programs that “perform a precise mathematical function such as sorting or finding the maximum of a sequence of numbers , determining primality, or finding the square root.”
A programmer should acquire good algorithms and idioms. (xiii)
- The authors express two major concerns:
- They want to establish the idea “idea that a computer language is not just a way of getting a computer to perform operations but rather that it is a novel formal medium for expressing ideas about methodology” (my emphasis).
- The essential material of interest here are the techniques used to control the intellectual complexity of large software systems; not: matters of syntax of particular languages, clever algorithms in special contexts, mathematical analysis of algorithms, or foundations of computing.
- Computer science is not science and its significance has very little to do with computers.
- Procedural Epistemology: “the study of the structure of knowledge from an imperative point of view, as opposed to a more declarative point of view…”.
- A Computational process is an abstract thing that inhabits a computer.
- Data are other abstract things manipulated by processes.
- A program is a pattern of rules that direct the evolution of a process.
- Programs are composed from expressions in programming languages.
- Good design is modular.
- Lisp interpreter: “a machine that carries out processes described in the Lisp language”.
- “…Lisp descriptions of processes, called procedures, can themselves be represented and manipulated as Lisp data. The importance of this is that there are powerful program-design techniques that rely on the ability to blur the traditional distinction between “passive” data and “active” processes.”
- A powerful programming language enables us to describe processes and organize our ideas about them, not merely to instruct a computer to perform some operations.
- To organize our ideas about processes well we must be able to
combine simple ideas to give life to more complex ones. We can do so
through three mechanisms provided by a powerful programming
language:
- Primitive expressions
- Means of combinations
- Means of abstractions
- “You type an expression, and the interpreter responds by displaying the result of its evaluating that expression.”
- Combinations;
- Operator;
- Operands;
- Arguments.
- read-eval-print loop: “the intepreter always operates in the same basic cycle: It reads an expression from the terminal, evaluates the expression, and prints the result”.
- A programming language provides means to use names to refer to computational object. “We say that the name identifies a variable whose value is the object.”
- “
Defineis our language’s simples means of abstraction. - Environment.
- The interpreter evaluates combinations by following a procedure:
- To evaluate a combination, do the following:
- Evaluate the subexpressions of the combination;
- Apply the procedure that is the value of the leftmost subexpression (the operator) to the arguments that are the values of the other subexpressions (the operands).
- To evaluate a combination, do the following:
- The evaluation rule is recursive.
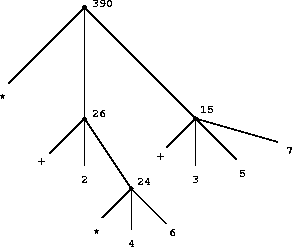
- We can view the evaluation in terms of a tree (See p. 10).
- Tree accumulation.
- Special forms constitute exceptions to the general evaluation
rule.
Defineis a special form.
- Procedure definitions: a much more powerful abstraction technique.
- Compound procedures.
- Application process for compound procedures:
- To apply a compound procedure to arguments, evaluate the body of the procedure with each formal parameter replaced by the corresponding argument.
- Substitution model for procedure application: a model to determine
the “meaning” of procedure application (in this chapter);
- This is not how interpreters actually work;
- The substitution model is the first of a sequence of increasingly elaborated models presented in this book of how intepreters work. Chapter 5 will present a complete implemetation of an interpreter an compiler.
- Lisp uses applicative-order evaluation: the interpreter evaluates the operator and the operands and then applies the resulting procedure to the resulting arguments — the procedure (followed by the intepreter to evaluate a combination) described above.
- An alternative evaluation mode: normal-order evaluation.
condifandornot
Exercise:
Below is a sequence of expressions. What is the result printed by the interpreter in response to each expression? Assume that the sequence is to be evaluated in the order in which it is presented.
10 (+ 5 3 4) (- 9 1) (/ 6 2) (+ (* 2 4) (- 4 6)) (define a 3) (define b (+ a 1)) (+ a b (* a b)) (= a b) (if (and (> b a) (< b (* a b))) b a) (cond ((= a 4) 6) ((= b 4) (+ 6 7 a)) (else 25)) (+ 2 (if (> b a) b a)) (* (cond ((> a b) a) ((< a b) b) (else -1)) (+ a 1))
Answer:
10
;; 10
(+ 5 3 4)
;; 12
(- 9 1)
;; 8
(/ 6 2)
;; 3
(+ (* 2 4) (- 4 6))
;; 6The authors, p. 8 fn. 8, say that the response to evaluating definitions is “highly implementation-dependent”.
I gather that Scheme’s define, when used for variables, is
equivalent for Elisp’s setq.
(setq a 3)
;; 3
(setq b (+ a 1))
;; 4
(+ a b (* a b))
;; 19I gather that Scheme’s =, when used for variables, is
equivalent for Elisp’s eq.
(eq a b)
;; nil
(if (and (> b a) (< b (* a b)))
b
a)
;; 4
(cond ((= a 4) 6)
((= b 4) (+ 6 7 a))
(else 25))
;; 16
(+ 2 (if (> b a) b a))
;; 6
(* (cond ((> a b) a)
((< a b) b)
(else -1))
(+ a 1))
;; 16Exercise:
Translate the following expression into prefix form
$\frac{5 + 4 + (2 - (3 - (6 + \frac{4}{5})))}{3(6 - 2)(2 - 7)}$
Answer:
(/ (+ 5
4
(- 2
(- 3
(+ 6
(/ 4 5)))))
(* 3
(- 6 2)
(- 2 7)))Exercise:
Define a procedure that takes three numbers as arguments and returns the sum of the squares of the two larger numbers.
Answer:
This was my first solution:
(defun foo (a b c)
(+ (square (if (> a b) a b))
(square (if (> c
(if (> a b) b a))
c
(if (> a b) b a)))))That works, although it is not ideal, because the combination (> a
b) is evaluated three times…
Exercise:
Observe that our model of evaluation allows for combinations whose operators are compound expressions. Use this observation to describe the behavior of the following procedure:
(define (a-plus-abs-b a b) ((if (> b 0) + -) a b))
Answer:
Behavior: If b is greater than 0, then apply + to a and b,
that is, add b to a. Otherwise, apply - to a and b, that is,
to subtract b from a.
But subtracting a negative number, means adding it! So, behavior: Add
the absolute value of b to a.
Exercise:
Ben Bitdiddle has invented a test to determine whether the interpreter he is faced with is using applicative-order evaluation or normal-order evaluation. He defines the following two procedures:
(define (p) (p)) (define (test x y) (if (= x 0) 0 y))Then he evaluates the expression
(test 0 (p))What behavior will Ben observe with an interpreter that uses applicative-order evaluation? What behavior will he observe with an interpreter that uses normal-order evaluation? Explain your answer. (Assume that the evaluation rule for the special form if is the same whether the interpreter is using normal or applicative order: The predicate expression is evaluated first, and the result determines whether to evaluate the consequent or the alternative expression.)
Answer:
In the case of applicative-order evaluation, “the interpreter first
evaluates the operator and operands and then applies the resulting
procedure to the resulting arguments” (p. 16). This means that the
interpreter will evaluate test, then 0 and then (p). test
evaluates to a procedure. 0 evaluates to 0. But (p) evaluates to
(p), which evaluates to (p), which evaluates to (p)’, which… ad
infinitum. So, the interpreter enters an infinite evaluation; it will
never be able to apply the procedure denoted by test, because it
will never be able to compute the second argument.
In the case of normal-order evaluation, operands are not evaluated
until their values are needed. (test 0 (p)) would be turned into 0
and then evaluated. And ‘0’ evaluates to 0.
- Procedures are analogous to mathematical functions: “[t]hey specify a value that is determined by one or more parameters”. (21-22)
- However, procedures are different from mathematical functions in
some respects. A mathematical function can tell us, say, whether a
certain number is the square root of
xor not. That, however, does not describe a procedure. It does not tell us how to find the square root ofx. - More generally, mathematics is usually concerned with “declarative knowledge”, whereas computer science is concerned with “imperative knowledge”.
- Iteration can be accomplished by calling a procedure. We don’t need any looping construct.
Exercise:
Alyssa P. Hacker doesn’t see why
ifneeds to be provided as a special form. “Why can’t I just define it as an ordinary procedure in terms ofcond?” she asks. Alyssa’s friend Eva Lu Ator claims this can indeed be done, and she defines a new version ofif:(define (new-if predicate then-clause else-clause) (cond (predicate then-clause) (else else-clause)))Eva demonstrates the program for Alyssa:
(new-if (= 2 3) 0 5) 5(new-if (= 1 1) 0 5) 0Delighted, Alyssa uses
new-ifto rewrite the square-root program:(define (sqrt-iter guess x) (new-if (good-enough? guess x) guess (sqrt-iter (improve guess x) x)))What happens when Alyssa attempts to use this to compute square roots? Explain.
Answer:
cond is a special form. if, too, is a special form. new-if,
instead, is not a special form. It is an ordinary combination.
Now, the evaluation of a combination entails the evaluation of both
the operator and the operands. With Eva’s new-if, then,
sqrt-iter calls itself ad infinitum and a stack overflow occurs.
In fact, if we replace the new-if — a combination — with the
cond — a special form — it would evaluate to, then things will
work as originally intended.
The
good-enough?test used in computing square roots will not be very effective for finding the square roots of very small numbers. Also, in real computers, arithmetic operations are almost always performed with limited precision. This makes our test inadequate for very large numbers. Explain these statements, with examples showing how the test fails for small and large numbers. An alternative strategy for implementinggood-enough?is to watch how guess changes from one iteration to the next and to stop when the change is a very small fraction of the guess. Design a square-root procedure that uses this kind of end test. Does this work better for small and large numbers?
Answer:
This is a pretty small number:
Let’s try to apply our test to the right answer divided by two.
(good-enough? (/ 0.0158113883 2) 0.00025)The test returns true; that is, it’s telling us that half of the right answer is good enough. I take that as a failure.
When we are dealing with very small numbers, then the
This is a pretty big number:
Let’s see whether are test consider the right answer as good enough…
(good-enough? 88851.3434339 7894561230.0)This evaluate to nil… The problem seems to lie in the application
of (the procedure named by) square, which gives a rather imprecise
result.
This is the body of good-enough?:
(< (abs (- (square 88851.3434339) 7894561230.0)) 0.001)It evaluates to nil, because the difference between the square of
the guess and the radicant is greater than 0.001. However, the
actual square of the radicant does not differ from the radicant of a
value greater than 0.001.
Here is my version of an improved version of good-enough? following
the authors’ suggestion:
(defun good-enough-improved? (new-guess old-guess)
(< (abs (- (abs old-guess) (abs new-guess))) (/ old-guess 10000000.0)))
(defun sqrt-iter2 (new-guess old-guess x)
(if (good-enough-improved? new-guess old-guess)
new-guess
(sqrt-iter2 (improve new-guess x) new-guess x)))
(defun sqrt2 (x)
(sqrt-iter2 1.0 x x))My version seems to work much better for small numbers:
(sqrt 0.00025) ;; => 0.033869844451165365
;; bad!
(sqrt2 0.00025) ;; => 0.015811388300841896
;; As good as the built-in emacs lisp sqrt function!But there doesn’t seem to be no difference with big numbers:
(sqrt 7894561230.0) ;; 88851.34343385023
(sqrt2 7894561230.0) ;; 88851.34343385023This is so, I think, because, even if good-enough? returns nil
when it shouldn’t, improve is called until we get something that
differs from the radicant for less than 0.001… is this correct?
Exercise:
Newton’s method for cube roots is based on the fact that if
$y$ is an approximation to the cube root of$x$ , then a better approximation is given by the value$\frac{x/y^2 + 2y}{3}$ . Use this formula to implement a cube-root procedure analogous to the square-root procedure. (In 1.3.4 we will see how to implement Newton’s method in general as an abstraction of these square-root and cube-root procedures.)
Answer:
(defun cuberoot (x)
(cuberoot-iter2 1.0 x x))
(defun cuberoot-iter (new-guess old-guess x)
(if (good-enough-improved? new-guess old-guess)
new-guess
(cuberoot-iter2 (improve-cr new-guess x) new-guess x)))
(defun improve-cr (guess x)
(/ (+ (/ x (square guess))
(* 2 y))
3))
- Analogy with chess. Mastering the rules doesn’t make you a master player. So far, we have only learnt the rules.
- To become expert programmers, we must learn to visualize the processes generated by various procedures. (Analogy with photography.)
- “A procedure is a pattern for the local evolution of a computational process”.
- Making statements about the global behavior of a process (whose local evolution has been specified by a procedure) is a difficult task.
- We can try to describe some typical patterns of process evolution.
- In this section we will:
- examine some common processes’ “shapes”;
- investigate the rate at which these processes consume computational resources (space and time).
One way to compute factorials:
(define (factorial n)
(if (= n 1)
1
(* n (factorial (- n 1)))))Using the substitution model we can “watch this procedure in action” (computing 6!):
(factorial 6)
(* 6 (factorial 5))
(* 6 (* 5 (factorial 4)))
(* 6 (* 5 (* 4 (factorial 3))))
(* 6 (* 5 (* 4 (* 3 (factorial 2)))))
(* 6 (* 5 (* 4 (* 3 (* 2 (factorial 1))))))
(* 6 (* 5 (* 4 (* 3 (* 2 1)))))
(* 6 (* 5 (* 4 (* 3 2))))
(* 6 (* 5 (* 4 6)))
(* 6 (* 5 24))
(* 6 120)
720Here is another way to compute the factorial:
(define (factorial n)
(fact-iter 1 1 n))
(define (fact-iter product counter max-count)
(if (> counter max-count)
product
(fact-iter (* counter product)
(+ counter 1)
max-count)))Let’s “visualize the process” (of computing 6!):
(factorial 6)
(fact-iter 1 1 6)
(fact-iter 1 1 6)
(fact-iter 6 2 6)
(fact-iter 12 3 6)
(fact-iter 36 4 6)
(fact-iter 144 5 6)
(fact-iter 720 6 6)
720- Both processes:
- compute the same mathematical function on the same domain;
- require a number of steps proportional to
nto computen!.
- However, we can notice a difference in “shape” between the ways
the two processes evolve.
- The first process is recursive process. Its evolutions shows
expansion and contraction. Expansion corresponds to deferred
operations. Contraction corresponds to performed
operations. The latter are to be kept track of. The amount of
information we need to keep track of is proportionial to
n— it grows linearly withn. This recursive process is therefore said to be linear. - The second process is an iterative process. The state of such a
process can summarized in terms of a fixed number of state
variables and the fixed rules to update those variables when
moving from one state to the next one, and, optionally, the
condition under which the process should terminate. We can see
that the number of steps grows linearly with
n. This iterative process is therefore said to be linear.
- The first process is recursive process. Its evolutions shows
expansion and contraction. Expansion corresponds to deferred
operations. Contraction corresponds to performed
operations. The latter are to be kept track of. The amount of
information we need to keep track of is proportionial to
- Another way to see the difference between the two processes: “In the iterative case, the program variables provide a complete description of the state of the process at any point”. In the recursive case, some “hidden information” is maintained by the interpreter.
- Let’s not confuse the notion of a recursive process with that of a recursive procedure.
- Tail recursion.
Each of the following two procedures defines a method for adding two positive integers in terms of the procedures inc, which increments its argument by 1, and dec, which decrements its argument by 1.
(define (+ a b) (if (= a 0) b (inc (+ (dec a) b)))) (define (+ a b) (if (= a 0) b (+ (dec a) (inc b))))Using the substitution model, illustrate the process generated by each procedure in evaluating (+ 4 5). Are these processes iterative or recursive?
(+ 4 5)
(inc (+ 3 5))
(inc (inc (+ 2 5)))
(inc (inc (inc (+ 1 5))))
(inc (inc (inc (inc (+ 0 5)))))
(inc (inc (inc (inc 5))))
(inc (inc (inc 6)))
(inc (inc 7))
(inc 8)
9Judging by its shape, it looks like we are dealing with a recursive process!
(+ 4 5)
(+ 3 6)
(+ 2 7)
(+ 1 8)
(+ 0 9)
9Judging by its shape, it looks like we are dealing with an iterative process!
Exercise:
The following procedure computes a mathematical function called Ackermann’s function.
(define (A x y) (cond ((= y 0) 0) ((= x 0) (* 2 y)) ((= y 1) 2) (else (A (- x 1) (A x (- y 1))))))What are the values of the following expressions?
(A 1 10) (A 2 4) (A 3 3)Consider the following procedures, where A is the procedure defined above:
(define (f n) (A 0 n)) (define (g n) (A 1 n)) (define (h n) (A 2 n)) (define (k n) (* 5 n n))Give concise mathematical definitions for the functions computed by the procedures
$f$ ,$g$ , and$h$ for positive integer values of$n$ . For example,$(k n)$ computes$5n^2$ .
Answer:
;; let's see the evolution of (A 1 10):
(A 1 10)
(A 0 (A 1 9))
(A 0 (A 0 (A 1 8)))
(A 0 (A 0 (A 0 (A 1 7))))
(A 0 (A 0 (A 0 (A 0 (A 1 6)))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 1 5))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 4)))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 3))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 2)))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 1))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 2)))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 4))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 8)))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 16))))))
(A 0 (A 0 (A 0 (A 0 (A 0 32)))))
(A 0 (A 0 (A 0 (A 0 64))))
(A 0 (A 0 (A 0 128)))
(A 0 (A 0 256))
(A 0 512)
1024
;; We are looking at a recursive process. The answer is 1024.
;; Let's do the same with (A 2 4).
(A 2 4)
(A 1 (A 2 3))
(A 1 (A 1 (A 2 2)))
(A 1 (A 1 (A 1 (A 2 1))))
(A 1 (A 1 (A 1 2)))
(A 1 (A 1 (A 0 (A 1 1))))
(A 1 (A 1 (A 0 2)))
(A 1 (A 1 4))
(A 1 (A 0 (A 1 3)))
(A 1 (A 0 (A 0 (A 1 2))))
(A 1 (A 0 (A 0 (A 0 (A 1 1)))))
(A 1 (A 0 (A 0 (A 0 2))))
(A 1 (A 0 (A 0 4)))
(A 1 (A 0 8))
(A 1 16)
(A 0 (A 1 15))
(A 0 (A 0 (A 1 14)))
(A 0 (A 0 (A 0 (A 1 13))))
(A 0 (A 0 (A 0 (A 0 (A 1 12)))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 1 11))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 10)))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 9))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 8)))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 7))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 6)))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 5))))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 4)))))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 3))))))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 2)))))))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 1 1))))))))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 2)))))))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 4))))))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 8)))))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 16))))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 32)))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 64))))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 128)))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 256))))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 (A 0 512)))))))
(A 0 (A 0 (A 0 (A 0 (A 0 (A 0 1024))))))
(A 0 (A 0 (A 0 (A 0 (A 0 2048)))))
(A 0 (A 0 (A 0 (A 0 4096))))
(A 0 (A 0 (A 0 8192)))
(A 0 (A 0 16384))
(A 0 32768)
65536
;; interesting shape... the answer is 65536;; Let's see now the evolution of (A 3 3):
(A 3 3)
(A 2 (A 3 2))
(A 2 (A 2 (A 3 1)))
(A 2 (A 2 2))
(A 2 (A 1 (A 2 1)))
(A 2 (A 1 2))
(A 2 (A 0 (A 1 1)))
(A 2 (A 0 2))
(A 2 4) ;; We already know this one!
65536(f 1) is 2:
(f 1)
(A 0 1)
2(f 2) is 4:
(f 2)
(A 0 2)
4(f 3) is 6:
(f 3)
(A 0 3)
(A 6)I conclude that (f n) computes
(g 1) is 2:
(g 1)
(A 1 1)
2(g 2) is 4:
(g 2)
(A 1 2)
(A 0 (A 1 1))
(A 0 2)
4(g 3) is 8:
(g 3)
(A 1 3)
(A 0 (A 1 2)) ;; we already know that (A 1 2) is 4
(A 0 4)
8(g 4) is 16:
(g 4)
(A 1 4)
(A 0 (A 1 3)) ;; we already know that (A 1 3) is 8
(A 0 8)
16Those are the powers of two. I conclude that (g n) computes
(h 1) is 2:
(h 1)
(A 2 1)
2(h 2) is 4:
(h 2)
(A 2 2)
(A 1 (A 2 1))
(A 1 2)
(A 0 (A 1 1))
(A 0 2)
4(h 3) is 16:
(h 3)
(A 2 3)
(A 1 (A 2 2))
(A 1 (A 1 (A 2 1)))
(A 1 (A 1 2))
(A 1 (A 0 (A 1 1)))
(A 1 (A 0 2))
(A 1 4) ;; we already know that (A 1 4) is 16
16(h 4) is 65536.
(h 4)
(A 2 4) ;; we know this one already...
65536(h 5) is
(h 5)
(A 2 5)
(A 1 (A 2 4)) ;; (A 2 4) is 65536
(A 1 65536)
(A 0 (A 1 65535))
(A 0 (A 0 (A 1 65635))) ;; oh oh... this would take a while...(h 4) is (h 3) is (h 2) is (h
n) computes $n(h (1- n)))$ where `(h (1- n))` is the application
of h to n minus 1.
(define (count-change amount)
(cc amount 5))
(define (cc amount kinds-of-coins)
(cond ((= amount 0) 1)
((or (< amount 0) (= kinds-of-coins 0)) 0)
(else (+ (cc amount
(- kinds-of-coins 1))
(cc (- amount
(first-denomination kinds-of-coins))
kinds-of-coins)))))
(define (first-denomination kinds-of-coins)
(cond ((= kinds-of-coins 1) 1)
((= kinds-of-coins 2) 5)
((= kinds-of-coins 3) 10)
((= kinds-of-coins 4) 25)
((= kinds-of-coins 5) 50)))- I wonder: what is an example of non-linear iteration?
Exercise:
A function f is defined by the rule that
$f(n) = n$ if $n <3 $ and$f(n) = f(n−1) + 2f(n−2) + 3f(n−3)$ if$n \geq 3$ . Write a procedure that computes$f$ by means of a recursive process. Write a procedure that computes$f$ by means of an iterative process.
Answer:
Writing a procedure that computes f by means of a recursive process
is quite straightforward.
(defun f (n)
(cond
((< n 3) n)
(t (+ (f (- n 1))
(* 2 (f (- n 2)))
(* 3 (f (- n 3)))))))
(f 0) ;; 0
(f 1) ;; 1
(f 2) ;; 2
(f 3) ;; 4
(f 4) ;; 11
(f 5) ;; 25Writing a (recursive) procedure that computes f by means of an
iterative process is less straightforward.
My thought process: up to 2 we know the answer; the answer is the very
same input. For a number n greater than 2, we are able to compute
the answer if we know the result for the inputs n - 1, n - 2, and
n - 3. In the case of of number 3 — the first number greater than
2 — we do know the answer for the inputs 3-1, 3-2, and 3-3. They
are, respectively, 2, 1, and 0. Given that we know that we can compute
the value of the function given input 3: .... But now we have the
enough knowledge to compute the value of the function given the
input 4. And once we know that… etc.
So we can use a counter that starts from 0 and iterate until we have done the right number of “loops”, keeping track of the three relevant values that allows us to compute the value of the process at that time.
(defun f2 (n)
(f-iter 0 n 0 1 2))
(defun f-iter (counter max-count A B C)
(if (< counter max-count) ;; keep iterating
(if (< counter 3)
(f-iter (1+ counter) max-count 0 1 2)
(f-iter (1+ counter) max-count B C (+ (* 3 A)
(* 2 B)
C)))
(if (< counter 3)
counter
(+ (* 3 A)
(* 2 B)
C))))
(f2 0) ;; 0
(f2 1) ;; 1
(f2 2) ;; 2
(f2 3) ;; 4
(f2 4) ;; 11
(f2 5) ;; 25Exercise:
....
Answer:
Here is an iterative solution in js I could quickly come up with:
function tartaglia(n) {
let previousLine = [1, 1,];
for (let i = 0; i < n; i++) {
if (i == 0) {
console.log( [1] )
} else if (i == 1) {
console.log( [1, 1] );
} else {
previousLine = line(previousLine);
console.log(previousLine);
}
}
}
//Compute line given previous one
function line(arr) {
let result = [1, ];
for (let i = 0; i < arr.length-1; i++) {
result.push(arr[i] + arr[i+1]);
}
result.push(1);
return result;
}
tartaglia(5);
// =>
// [ 1 ]
// [ 1, 1 ]
// [ 1, 2, 1 ]
// [ 1, 3, 3, 1 ]
// [ 1, 4, 6, 4, 1 ]So… after too much thinking, while brushing my teeth and almost in bed, I came up with a solution.
You can think of the triangle just as a bunch of lines/rows, each of which is one element more than the previous one.
a b, c d, e, f g, h, i, j ...
What helped me to find a solution was using a row[col] notation.
0[0] 1[0], 1[1] 2[0], 2[1], 2[2] 3[0], 3[1], 3[2], 3[3] 4[0], 4[1], 4[2], 4[3], 4[4]
We can immediately notice two things:
- first, col=0 means we are dealing with the first element of a row. But the first element of a row is always a 1.
- second, when row=col we are dealing with the last element of a row. But the last element of a row is always a 1.
Finally, we need a way to find the value of those elements where neither row≠col nor col=0. Saying that an element equals the sum of the two numbers “above” it is equivalent to say that an element with inidex i at row r is equal to the sum of two elements at row r-1, more specifically to the sum of those two elements the first one of which has index i-1 and the second one of which has index i.
We have enough rules.
;;(tartaglia row col)
;;
;;col=0 ==> 1
;;col=row ==> 1
;;else ==> (+ (tartaglia (1- row)(1- col))
;; (tartaglia (1- row) col))We can write our procedure!
(defun tartaglia (r c)
(cond
((= c 0) 1)
((= r c) 1)
(t (+ (tartaglia (1- r)(1- c))
(tartaglia (1- r) c)))))
(tartaglia 0 0)
;; => 1
(tartaglia 1 0) (tartaglia 1 1)
;; => 1, 1
(tartaglia 2 0) (tartaglia 2 1) (tartaglia 2 2)
;; => 1, 2, 1
(tartaglia 3 0) (tartaglia 3 1) (tartaglia 3 2) (tartaglia 3 3)
;; => 1, 3, 3, 1
(tartaglia 4 0) (tartaglia 4 1) (tartaglia 4 2) (tartaglia 4 3) (tartaglia 4 4)
;; 1, 4, 6, 4, 1It works!
Exercise:
Draw the tree illustrating the process generated by the count-change procedure of 1.2.2 in making change for 11 cents. What are the orders of growth of the space and number of steps used by this process as the amount to be changed increases?
Answer: Here how the process looks like when using the substitution model:
(defun count-change (amount)
(cc amount 5))
(defun cc (amount kinds-of-coins)
(cond ((= amount 0) 1)
((or (< amount 0)
(= kinds-of-coins 0))
0)
(t
(+ (cc amount (- kinds-of-coins 1))
(cc (- amount (first-denomination
kinds-of-coins))
kinds-of-coins)))))
(defun first-denomination (kinds-of-coins)
(cond ((= kinds-of-coins 1) 1)
((= kinds-of-coins 2) 5)
((= kinds-of-coins 3) 10)
((= kinds-of-coins 4) 25)
((= kinds-of-coins 5) 50)))
(count-change 11)
(count-change 11)
(cc 11 5)
(+ (cc 11 (- 5 1))
(cc (- 11 (first-denomination
5))
5))
(+ (cc 11 4)
(cc -39 5))
(+ (cc 11 4)
0)
(+ (+ (cc 11 (- 4 1))
(cc (- 11 (first-denomination
4))
4))
0)
(+ (+ (cc 11 3)
(cc -14 4))
0)
(+ (+ (cc 11 3)
0)
0)
(+ (+ (+ (cc 11 (- 3 1))
(cc (- 11 (first-denomination
3))
3))
0)
0)
(+ (+ (+ (cc 11 2)
(cc 1 3))
0)
0)
(+ (+ (+ (+ (cc 11 (- 2 1))
(cc (- 11 (first-denomination
2))
2))
(+ (cc 1 (- 3 1))
(cc (- 1 (first-denomination
3))
3)))
0)
0)
(+ (+ (+ (+ (cc 11 1)
(cc 6 2))
(+ (cc 1 2)
(cc -9 3)))
0)
0)
(+ (+ (+ (+ (cc 11 1)
(cc 6 2))
(+ (cc 1 2)
0))
0)
0)
(+ (+ (+ (+ (+ (cc 11 (- 1 1))
(cc (- 11 (first-denomination
1))
1))
(+ (cc 6 (- 2 1))
(cc (- 6 (first-denomination
2))
2)))
(+ (+ (cc 1 (- 2 1))
(cc (- 1 (first-denomination
2))
2))
0))
0)
0)
(+ (+ (+ (+ (+ (cc 11 0)
(cc 10 1))
(+ (cc 6 1)
(cc 1 2)))
(+ (+ (cc 1 1)
(cc -4 2))
0))
0)
0)
(+ (+ (+ (+ (+ 0
(cc 10 1))
(+ (cc 6 1)
(cc 1 2)))
(+ (+ (cc 1 1)
0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ (cc 10 (- 1 1))
(cc (- 10 (first-denomination
1))
1)))
(+ (+ (cc 6 (- 1 1))
(cc (- 6 (first-denomination
1))
1))
(+ (cc 1 (- 2 1))
(cc (- 1 (first-denomination
2))
2))))
(+ (+ (+ (cc 1 (- 1 1))
(cc (- 1 (first-denomination
1))
1))
0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ (cc 10 0)
(cc 9 1)))
(+ (+ (cc 6 0)
(cc 5 1))
(+ (cc 1 1)
(cc -4 2))))
(+ (+ (+ (cc 1 0)
(cc 0 1))
0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(cc 9 1)))
(+ (+ 0
(cc 5 1))
(+ (cc 1 1)
0)))
(+ (+ (+ 0
1)
0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(cc 9 1)))
(+ (+ 0
(cc 5 1))
(+ (cc 1 1)
0)))
(+ (+ 1
0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ (cc 9 (- 1 1))
(cc (- 9 (first-denomination
1))
1))))
(+ (+ 0
(+ (cc 5 (- 1 1))
(cc (- 5 (first-denomination
1))
1)))
(+ (+ (cc 1 (- 1 1))
(cc (- 1 (first-denomination
1))
1))
0)))
(+ (+ 1
0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ (cc 9 0)
(cc 8 1))))
(+ (+ 0
(+ (cc 5 0)
(cc 4 1)))
(+ (+ (cc 1 0)
(cc 0 1))
0)))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(cc 8 1))))
(+ (+ 0
(+ 0
(cc 4 1)))
(+ (+ 0 1)
0)))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(cc 8 1))))
(+ (+ 0
(+ 0
(cc 4 1)))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ (cc 8 (- 1 1))
(cc (- 8 (first-denomination
1))
1)))))
(+ (+ 0
(+ 0
(+ (cc 4 (- 1 1))
(cc (- 4 (first-denomination
1))
1))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ (cc 8 (- 1 1))
(cc (- 8 1) 1)))))
(+ (+ 0
(+ 0
(+ (cc 4 (- 1 1))
(cc (- 4 1) 1))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ (cc 8 0)
(cc 7 1)))))
(+ (+ 0
(+ 0
(+ (cc 4 0)
(cc 3 1))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0 (cc 7 1)))))
(+ (+ 0
(+ 0
(+ 0 (cc 3 1))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0 (+ (cc 7 (- 1 1))
(cc (- 7 (first-denomination
1))
1))))))
(+ (+ 0
(+ 0
(+ 0 (+ (cc 3 (- 1 1))
(cc (- 3 (first-denomination
1))
1)))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0 (+ (cc 7 (- 1 1))
(cc (- 7 1)
1))))))
(+ (+ 0
(+ 0
(+ 0 (+ (cc 3 (- 1 1))
(cc (- 3 1)
1)))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0 (+ (cc 7 0)
(cc 6 1))))))
(+ (+ 0
(+ 0
(+ 0 (+ (cc 3 0)
(cc 2 1)))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0 (cc 6 1))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0 (cc 2 1)))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0 (+ (cc 6 (- 1 1))
(cc (- 6 (first-denomination
1))
1)))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0 (+ (cc 2 (- 1 1))
(cc (- 2 (first-denomination
1))
1))))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0 (+ (cc 6 (- 1 1))
(cc (- 6 1)
1)))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0 (+ (cc 2 (- 1 1))
(cc (- 2 1)
1))))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0 (+ (cc 6 0)
(cc 5 1)))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0 (+ (cc 2 0)
(cc 1 1))))))
1))
(+ (+ 1 0)
0))
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(cc 5 1)))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(cc 1 1))))))
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 5 (- 1 1))
(cc (- 5 (first-denomination
1))
1))))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 1 (- 1 1))
(cc (- 1 (first-denomination
1))
1)))))))
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 5 (- 1 1))
(cc (- 5 1)
1))))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 1 (- 1 1))
(cc (- 1 1)
1)))))))
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 5 0)
(cc 4 1))))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 1 0)
(cc 0 1)))))))
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(cc 4 1))))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0 1))))))
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 4 (- 1 1))
(cc (- 4 (first-denomination
1))
1)))))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0 1)))))
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 4 (- 1 1))
(cc (- 4 1)
1)))))))))
(+ (+ 0
(+ 0
(+ 0
(+ 0 1))))
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 4 0)
(cc 3 1)))))))))
(+ (+ 0
(+ 0
(+ 0 1)))
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(cc 3 1)))))))))
(+ (+ 0
(+ 0 1))
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 3 (- 1 1))
(cc (- 3 (first-denomination
1))
1))))))))))
(+ (+ 0 1)
1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 3 (- 1 1))
(cc (- 3 1)
1))))))))))
(+ 1 1))
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 3 0)
(cc (- 3 1)
1))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(cc 2 1))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 2 (- 1 1))
(cc (- 2 (first-denomination
1))
1)))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 2 (- 1 1))
(cc (- 2 1)
1)))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 2 0)
(cc 1 1)))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 1 (- 1 1))
(cc (- 1 (first-denomination
1))
1))))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 1 (- 1 1))
(cc (- 1 1)
1))))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ (cc 1 0)
(cc 0 1))))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0 1)))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0 1))))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0 1)))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0 1))))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0 1)))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0
(+ 0 1))))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0
(+ 0 1)))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0
(+ 0 1))))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0
(+ 0 1)))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0
(+ 0 1))
2)
1)
0)
0)
(+ (+ (+ (+ (+ 0 1)
2)
1)
0)
0)
(+ (+ (+ (+ 1 2)
1)
0)
0)
(+ (+ (+ 3 1)
0)
0)
(+ (+ 4 0)
0)
(+ 4 0)
4Analogously to what has been done at page 38 with fib, we can
represent tree generated by count-change in the following way:
(count-change 11)
(cc 11 5)
/ \
(cc 11 4) (cc - 39 5)
/ \ \
(cc 11 3) (cc -14 4) 0
/ \ \
(cc 11 2) (cc 1 3) 0
/ \ / \
(cc 11 1) (cc 6 2) (cc 1 2) (cc -9 3)
___| /\____ |_____ \
___/ | | | |____ \_______ \_____
| | | \ | | |
(cc 11 0) (cc 10 1) (cc 6 1) (cc 1 2) (cc 1 1) (cc -4 2) 0
___/ ____/ | /\ |\ |_________ \__________
_____/ ___| / / \ | \_____ \_______ |______ |
| | / / | | | | | |
0 (cc 10 0) (cc 9 1) (cc 6 0) (cc 5 1) (cc 1 1) (cc -4 2) (cc 1 0) (cc 0 1) 0
/ /\ / / \ |\____ \ | |
__/ __/ \ / / \ | \___ \_____ | |
| / | | / \ | | | | |
0 (cc 9 0) (cc 8 1) 0 (cc 5 0) (cc 4 1) (cc 1 0) (cc 0 1) 0 0 1
| /\ | |\__ \ |
| / \ | | \ \ |
0 (cc 8 0) (cc 7 1) 0 (cc 4 0) (cc 3 1) 0 1
| /\ | /\
| / \ | / \
0 (cc 7 0) (cc 6 1) 0 (cc 3 0) (cc 2 1)
| /\ | /\
| / \ | / \
0 (cc 6 0) (cc 5 1) 0 (cc 2 0) (cc 1 1)
/ /\ / /\
/ / \ | / \
0 (cc 5 0) (cc 4 1) 0 (cc 1 0) (cc 0 1)
| /\ | |
| / \ | |
0 (cc 4 0) (cc 3 1) 0 1
| /\
| / \
0 (cc 3 0) (cc 2 1)
| /\
| / \
0 (cc 2 0) (cc 1 1)
| /\
| / \
0 (cc 1 0) (cc 0 1)
| |
0 1
This looks like a tree recursive processe like that of fib. And
In general, the number of steps required by a tree-recursive process will be proportional to the number of nodes in the tree, while the space required will be proportional to the maximum depth of the tree (p.39).
So the order of growth in time of count-change is
Exercise:
The sine of an angle (specified in radians) can be computed by making use of the approximation $sin x ≈ x$if
$x$ is sufficiently small, and the trigonometric identity
$sin x = 3 sin \frac{x}{3} - 4 sin^3 \frac{x}{3}$ to reduce the size of the argument of
$sin$ . (For purposes of this exercise an angle is considered “sufficiently small” if its magnitude is not greater than 0.1 radians.) These ideas are incorporated in the following procedures:(define (cube x) (* x x x)) (define (p x) (- (* 3 x) (* 4 (cube x)))) (define (sine angle) (if (not (> (abs angle) 0.1)) angle (p (sine (/ angle 3.0)))))
- How many times is the procedure p applied when
(sine 12.15)is evaluated?- What is the order of growth in space and number of steps (as a function of
a) used by the process generated by thesineprocedure when(sine a)is evaluated?
Answer:
(defun cube (x) (* x x x))
(defun p (x) (- (* 3 x) (* 4 (cube x))))
(defun sine (angle)
(if (not (> (abs angle) 0.1))
angle
(p (sine (/ angle 3.0)))))(defun cube (x) (* x x x))
(defun p (x) (- (* 3 x) (* 4 (cube x))))
(defun sine (angle)
(if (not (> (abs angle) 0.1))
angle
(p (sine (/ angle 3.0)))))
(sine 12.15) ;; -0.39980345741334
(p (sine (/ 12.15 3.0)))
(p (sine 4.05))
(p (p (sine (/ 4.05 3.0))))
(p (p (sine 1.3499999999999999)))
(p (p (p (sine (/ 1.3499999999999999 3.0)))))
(p (p (p (sine 0.44999999999999996))))
(p (p (p (p (sine (/ 0.44999999999999996 3.0))))))
(p (p (p (p (sine 0.15)))))
(p (p (p (p (p (sine (/ 0.15 3.0)))))))
(p (p (p (p (p (sine 0.049999999999999996))))))
(p (p (p (p (p (sine 0.049999999999999996))))))
(p (p (p (p (p 0.049999999999999996)))))
(p (p (p (p (- (* 3 0.049999999999999996) (* 4 (cube 0.049999999999999996)))))))
(p (p (p (p 0.1495))))
(p (p (p 0.4351345505)))
(p (p 0.9758465331678772))
(p -0.7895631144708228)
(- -2.3686893434124685 -1.9688858859991285)
-0.39980345741334- Procedure
pis applied five times. - I tentatively thought that the order of growth in space and time
was O(n).
However I’ve looked arout at other people’s solutions and that is not right. The order of growth is better than linear; it’s logarithmic, O(log(n)); more specifically O(log3(n)). I definitively need to revive my math skills, assuming they still exist somewhere.
This was the most intuitive explanation I’ve found of why that is so: “the amount of times
pis evaluated is incremented by one for every tripling ofa. […] As for the order of growth regarding space, it should be the same as for the number of steps, because for each additional step, there is exactly one more function call that the system must keep track of” (https://www.timwoerner.de/posts/sicp/exercises/1/15/)
(defun expt (b n)
(if (= n 0)
1
(* b (expt b (- n 1)))))This requires ϴ(n) steps and ϴ(n) space.
We have have already seen such a kind of process (linear recursion) with factorial. JUst as with factorial, we can write a procedurs that evolves a linear iterative process:
(defun expt-iter (b counter product)
(if (= counter 0)
product
(expt-iter b
(- counter 1)
(* b product))))This process requires ϴ(n) steps and ϴ(1) space.
We can be faster.
(defun fast-expt (b n)
(cond ((= n 0)
1)
((even? n)
(square (fast-expt b (/ n 2))))
(t
(* b (fast-expt b (- n 1))))))
(defun (even? n)
(= (remainder n 2) 0))fast-expt evolves a process that grows logarithmically with n in
both space and time.
Exercise:
Design a procedure that evolves an iterative exponentiation process that uses successive squaring and uses a logarithmic number of steps, as does
fast-expt. (Hint: Using the observation that $(bb/2)^2 = (b^2)n/2$, keep, along with the exponent n and the base b, an additional state variable a, and define the state transformation in such a way that the product abn is unchanged from state to state. At the beginning of the process a is taken to be 1, and the answer is given by the value of a at the end of the process. In general, the technique of defining an invariant quantity that remains unchanged from state to state is a powerful way to think about the design of iterative algorithms.)
Answer:
(defun fast-expt-i (b n)
(fast-expt-iter b n 1))
(defun fast-expt-iter (b n a)
(cond ((= n 0) a)
((even n)
(fast-expt-iter (square b) (/ n 2) a))
(t
(fast-expt-iter b (- n 1) (* b a)))))I’ve asked ChatGPT about whether it thought that this solution was correct. Here is the answer:
Yes, the provided implementation of the fast-expt-i function and the fast-expt-iter function appears to correctly compute the value of the exponentiation with base b and exponent n.
The fast-expt-i function is a wrapper function that calls the fast-expt-iter function with the initial value of a set to 1. The fast-expt-iter function is a recursive function that implements the exponentiation algorithm using a technique called “iterative deepening,” which allows for more efficient computation of exponentiation by repeatedly squaring the base and halving the exponent until the exponent becomes 0.
The cond statement in the fast-expt-iter function handles the base case where the exponent is 0, as well as the cases where the exponent is even or odd. In the case where the exponent is 0, the function returns the value of a, which is the result of the exponentiation. In the case where the exponent is even, the function calls itself with the square of the base and half the exponent, and in the case where the exponent is odd, the function calls itself with the base and the exponent decremented by 1.
Overall, the provided implementation appears to correctly compute the value of the exponentiation with base b and exponent n.
I’ve also asked about space complexity:
The order of growth in space of the fast-expt-i function is O(n), where n is the value of the exponent. This is because the function uses recursive calls to compute the exponentiation, and each recursive call requires additional space on the call stack to store the local variables and intermediate results.
In the case of the fast-expt-i function, the space required for each recursive call is constant, as it only stores the values of the base b, exponent n, and accumulator a variables. Therefore, the total space required by the function is proportional to the number of recursive calls, which is equal to the value of the exponent.
For example, if the exponent has a value of n, the function will require O(n) space to compute the result, as it will make n recursive calls. This is known as linear space complexity.
It is important to note that the space complexity of the fast-expt-i function can be improved by using a technique called “tail call optimization,” which allows the compiler to reuse the space on the call stack for the recursive calls, rather than allocating additional space for each call. This can reduce the space complexity of the function to O(1), as only a constant amount of space is required to store the local variables and intermediate results. However, this optimization is not performed by default in most Lisp implementations, and may require explicit support from the compiler or runtime environment.
The exponentiation algorithms in this section are based on performing exponentiation by means of repeated multiplication. In a similar way, one can perform integer multiplication by means of repeated addition. The following multiplication procedure (in which it is assumed that our language can only add, not multiply) is analogous to the expt procedure:
(define (* a b) (if (= b 0) 0 (+ a (* a (- b 1)))))This algorithm takes a number of steps that is linear in b. Now suppose we include, together with addition, operations double, which doubles an integer, and halve, which divides an (even) integer by 2. Using these, design a multiplication procedure analogous to fast-expt that uses a logarithmic number of steps.
Answer:
(defun double (a)
(* a 2))
(defun halve (a)
(/ a 2))
(defun fast-* (a b)
(cond ((= b 1) a)
((even b) (double (fast-* a (halve b))))
(t (+ a (fast-* a (- b 1))))))Exercise:
Using the results of Exercise 1.16 and Exercise 1.17, devise a procedure that generates an iterative process for multiplying two integers in terms of adding, doubling, and halving and uses a logarithmic number of steps (fn: This algorithm, which is sometimes known as the “Russian peasant method” of multiplication, is ancient. Examples of its use are found in the Rhind Papyrus, one of the two oldest mathematical documents in existence, written about 1700 B.C. (and copied from an even older document) by an Egyptian scribe named A’h-mose.)
Answer
(defun fast-*-i (a b)
(fast-*-iter a b 0))
(defun fast-*-iter (a b c)
(cond ((= c 0) 0)
((even b) (fast-*-iter (double a) (halve b) c))
(t (fast-*-iter a (- b 1) (+ a c))There is a clever algorithm for computing the Fibonacci numbers in a logarithmic number of steps. Recall the transformation of the state variables a and b in the fib-iter process of 1.2.2:
$a ← a + b$ and$b ← a$ . Call this transformation$T$ , starting with the pair (1, 0). Now consider$T$ to be the special case of$p = 0$ and$q = 1$ in a family of transformation $Tpq$, where $Tpq$ transforms the pair$(a, b)$ according to$a ← bq + aq + ap$ and$b ← bp + aq$ . Show that if we apply such a transformation $Tpq$ twice, the effect is the same as using a single transformation $Tp’q’$ of the same form, and computer$p’$ and$q’$ in terms of$p$ and$q$ . This gives us an explicit way to square these transformations, and thus we can compute$T^n$ using successive squaring, as in thefast-exptprocedures. Put this all together to complete the following procedure, which runs in a logarithmic number of steps:
(define (fib n)
(fib-iter 1 0 0 1 n))
(define (fib-iter a b p q count)
(cond ((= count 0)
b)
((even? count)
(fib-iter a
b
⟨??⟩ ;compute p'
⟨??⟩ ;compute q'
(/ count 2)))
(else
(fib-iter (+ (* b q)
(* a q)
(* a p))
(+ (* b p)
(* a q))
p
q
(- count 1)))))
Exercise:
Exercise 1.20: The process that a procedure generates is of course dependent on the rules used by the interpreter. As an example, consider the iterative gcd procedure given above. Suppose we were to interpret this procedure using normal-order evaluation, as discussed in 1.1.5. (The normal-order-evaluation rule for if is described in Exercise 1.5.) Using the substitution method (for normal order), illustrate the process generated in evaluating (gcd 206 40) and indicate the remainder operations that are actually performed. How many remainder operations are actually performed in the normal-order evaluation of (gcd 206 40)? In the applicative-order evaluation?
Answer:
Let us repeat some older stuff.
Evaluation a combination (applicative order): The interpreter evaluates a combination by:
- Evaluating the subexpression of the combination (recursion!);
- Applying the procedure that is the value of the leftmost subexpression (the operator) to the arguments that are the values of the other subexpressions (the operands).
What does it mean to apply a procedure?
Procedure application: for primitive procedures we can assume that the mechanism is built into the interpreter. For compound procedurees: evaluate the body of the procedure with each formal parameter replaced by the corresponding argument. Given the replacing this is known as “substitution model”.
A different model:
Evaluation a combination (normal order evaluation): evaluate the operan only when needed
(defun gcd (a b)
(if (= b 0)
a
(gcd b (% a b))));; normal order evaluation
(gcd 206 40)
(if (= 40 0)
206
(gcd 40 (% 206 40)))
(gcd 40 (% 206 40)))
(if (= (% 206 40) 0) ;;1
40
(gcd (% 206 40) (% 40 (% 206 40))))
(gcd (% 206 40) (% 40 (% 206 40)))
(if (= (% 40 (% 206 40)) 0) ;; 2, 3
(% 206 40)
(gcd (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40)))))
(gcd (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40))))
(if (= (% (% 206 40) (% 40 (% 206 40))) 0) ;; 4, 5, 6, 7
(% 40 (% 206 40))
(gcd (% (% 206 40) (% 40 (% 206 40)))
(% (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40)))))))
(gcd (% (% 206 40) (% 40 (% 206 40)))
(% (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40)))))
(if (= (% (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40)))) 0) ;; 8, 9, 10, 11, 12, 13, 14
(% (% 206 40) (% 40 (% 206 40)))
(gcd (% (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40))))
(% (% (% 206 40) (% 40 (% 206 40))) (% (% 40 (% 206 40)) (% (% 206 40) (% 40 (% 206 40)))))))
(% (% 206 40) (% 40 (% 206 40))) ;; 15, 16, 17, 18;; applicative order evaluation
(defun gcd (a b)
(if (= b 0)
a
(gcd b (% a b))))
(gcd 206 40)
(if (= 40 0)
206
(gcd 40 (% 206 40)))
(gcd 40 (% 206 40)) ; 1
(gcd 40 6)
(if (= 6 0)
40
(gcd 6 (% 40 6)))
(gcd 6 (% 40 6)) ; 2
(gcd 6 4)
(if (= 4 0)
6
(gcd 4 (% 6 4)))
(gcd 4 (% 6 4)) ; 3
(gcd 4 2)
(if (= 2 0)
4
(gcd 2 (% 4 2)))
(gcd 2 (% 4 2)) ; 4
(gcd 2 0)
(if (= 0 0)
2
(gcd 0 (% 2 0)))
2Here is one way to find whether a number is prime:
(defun smallest-divisor (n)
(find-divisor n 2))
(defun find-divisor (n test-divisor)
(cond ((> (square test-divisor) n)
n)
((dividesp test-divisor n)
test-divisor)
(t (find-divisor
n
(+ test-divisor 1)))))
(defun dividesp (a b)
(= (% b a ) 0))
(defun primep (n)
(= n (smallest-divisor n)))In the worst case scenario we have to call test-divisor
The authors also present a
- Fermat’s Little Theorem: If
$n$ is a prime number and$a$ is any positive integer less than n, then$a$ raised ot the $nth$ power is congruent to$a$ modulo$n$ .
(defun expmod (base exp m)
(cond ((= exp 0) 1)
((evenp exp)
(%
(square (expmod base (/ exp 2) m))
m))
(t
(%
(* base (expmod base (- exp 1) m))
m))))
(defun try-it (a n)
(= (expmod a n n) a))
(defun fermat-test (n)
(try-it (+ 1 (random (- n 1))) n))
(defun fast-primep (n times)
(cond ((= times 0) t)
((fermat-test n)
(fast-primep n (- times 1)))
(t nil)))
(defun evenp (n)
(= (% n 2) 0)Exercise:
Use the smallest-divisor procedure to find the smallest divisor of each of the following numbers: 199, 1999, 19999.
Answer:
(smallest-divisor 199) ;; => 199This is the series of procedure calls:
(smallest-divisor 199)
(find-divisor 199 2)
(cond ((> (square 2) 199)
199)
((dividesp 2 199)
2)
(t (find-divisor
199
(+ 2 1))))
(find-divisor 199 3)
(find-divisor 199 4)
(find-divisor 199 5)
(find-divisor 199 6)
(find-divisor 199 7)
(find-divisor 199 8)
(find-divisor 199 9)
(find-divisor 199 10)
(find-divisor 199 11)
(find-divisor 199 12)
(find-divisor 199 13)
(find-divisor 199 14)
(find-divisor 199 15)
199(smallest-divisor 1999) ;; => 1999This is the series of procedure calls:
(smallest-divisor 1999)
(find-divisor 1999 2)
(cond ((> (square 2) 1999)
1999)
((dividesp 2 1999)
2)
(t (find-divisor
1999
(+ 2 1))))
(find-divisor 1999 3)
(find-divisor 1999 4)
;; ...
(find-divisor 1999 45)
1999(smallest-divisor 19999) ;; => 7This is the series of procedure calls:
(smallest-divisor 19999)
(find-divisor 19999 2)
(find-divisor 19999 3)
(find-divisor 19999 4)
(find-divisor 19999 5)
(find-divisor 19999 6)
(find-divisor 19999 7)
7Most Lisp implementations include a primitive called runtime that returns an integer that specifies the amount of time the system has been running (measured, for example, in microseconds). The following timed-prime-test procedure, when called with an integer n, prints n and checks to see if n is prime. If n is prime, the procedure prints three asterisks followed by the amount of time used in performing the test.
(define (timed-prime-test n) (newline) (display n) (start-prime-test n (runtime))) (define (start-prime-test n start-time) (if (prime? n) (report-prime (- (runtime) start-time)))) (define (report-prime elapsed-time) (display " *** ") (display elapsed-time))Using this procedure, write a procedure search-for-primes that checks the primality of consecutive odd integers in a specified range. Use your procedure to find the three smallest primes larger than 1000; larger than 10,000; larger than 100,000; larger than 1,000,000. Note the time needed to test each prime. Since the testing algorithm has order of growth of
$θ (\sqrt{n})$ , you should expect that testing for primes around 10,000 should take about$\sqrt{10}$ times as long as testing for primes around 1000. Do your timing data bear this out? How well do the data for 100,000 and 1,000,000 support the$θ (\sqrt{n})$ prediction? Is your result compatible with the notion that programs on your machine run in time proportional to the number of steps required for the computation?
Answer:
For this one I’m using (Dr)Racket, which provides a version of Scheme
specifically modified in order to be used for SICP’s code (useful here
in that it provides runtime).
#lang sicp
(define (square x)
(* x x))
(define (smallest-divisor n)
(find-divisor n 2))
(define (find-divisor n test-divisor)
(cond ((> (square test-divisor) n)
n)
((divides? test-divisor n)
test-divisor)
(else (find-divisor
n
(+ test-divisor 1)))))
(define (divides? a b)
(= (remainder b a) 0))
(define (prime? n)
(= n (smallest-divisor n)))
(define (timed-prime-test n)
(newline)
(display n)
(start-prime-test n (runtime)))
(define (start-prime-test n start-time)
(if (prime? n)
(report-prime (- (runtime)
start-time))))
(define (report-prime elapsed-time)
(display " *** ")
(display elapsed-time))
(timed-prime-test 199) ;; 199 *** 6(define (search-for-primes begin end)
(cond ((< begin end)
(timed-prime-test begin)
(search-for-primes (+ 2 begin) end))))(search-for-primes 1001 1021)
;; 1001
;; 1003
;; 1005
;; 1007
;; 1009 *** 5
;; 1011
;; 1013 *** 4
;; 1015
;; 1017
;; 1019 *** 3
(search-for-primes 10001 10050)
;; 10001
;; 10003
;; 10005
;; 10007 *** 12
;; 10009 *** 9
;; 10011
;; 10013
;; 10015
;; 10017
;; 10019
;; 10021
;; 10023
;; 10025
;; 10027
;; 10029
;; 10031
;; 10033
;; 10035
;; 10037 *** 8
;; 10039 *** 8
;; 10041
;; 10043
;; 10045
;; 10047
;; 10049
(search-for-primes 100001 100050)
;; 100001
;; 100003 *** 22
;; 100005
;; 100007
;; 100009
;; 100011
;; 100013
;; 100015
;; 100017
;; 100019 *** 21
;; 100021
;; 100023
;; 100025
;; 100027
;; 100029
;; 100031
;; 100033
;; 100035
;; 100037
;; 100039
;; 100041
;; 100043 *** 21
;; 100045
;; 100047
;; 100049 *** 20
(search-for-primes 1000001 1000051)
;; 1000001
;; 1000003 *** 79
;; 1000005
;; 1000007
;; 1000009
;; 1000011
;; 1000013
;; 1000015
;; 1000017
;; 1000019
;; 1000021
;; 1000023
;; 1000025
;; 1000027
;; 1000029
;; 1000031
;; 1000033 *** 63
;; 1000035
;; 1000037 *** 62
;; 1000039 *** 65
;; 1000041
;; 1000043
;; 1000045
;; 1000047
;; 1000049In today’s computers these operations take microseconds. I have been told that the accuracy of these measurements is not to be trusted, given the small size of these amounts of time.
We can, however, use biggers numbers.
Computing (timed-prime-test 34888314291653) — I’ve chosen randomly
— took 642.775 milliseconds. These should be more than enough to
have an acceptable accuracy in our benchmarking. Let’s start our
experiments from here.
Let’s find the first three primes starting from 34888314291653.
;; 34888314291653 *** 701102
;; 34888314291655
;; 34888314291657
;; 34888314291659
;; 34888314291661
;; 34888314291663
;; 34888314291665
;; 34888314291667 *** 895322
;; 34888314291669
;; 34888314291671
;; 34888314291673
;; 34888314291675
;; 34888314291677
;; 34888314291679
;; 34888314291681
;; 34888314291683
;; 34888314291685
;; 34888314291687
;; 34888314291689
;; 34888314291691
;; 34888314291693
;; 34888314291695
;; 34888314291697
;; 34888314291699
;; 34888314291701
;; 34888314291703
;; 34888314291705
;; 34888314291707
;; 34888314291709
;; 34888314291711
;; 34888314291713 *** 630255Now we multiply 34888314291653 by ten and find the first three primes starting from there. 34888314291653 times 10 is 348883142916530.
;; 348883142916531
;; 348883142916533 *** 2027795
;; 348883142916535
;; 348883142916537
;; 348883142916539
;; 348883142916541
;; 348883142916543
;; 348883142916545
;; 348883142916547
;; 348883142916549
;; 348883142916551
;; 348883142916553
;; 348883142916555
;; 348883142916557
;; 348883142916559
;; 348883142916561
;; 348883142916563
;; 348883142916565
;; 348883142916567
;; 348883142916569
;; 348883142916571
;; 348883142916573
;; 348883142916575
;; 348883142916577
;; 348883142916579
;; 348883142916581
;; 348883142916583
;; 348883142916585
;; 348883142916587
;; 348883142916589
;; 348883142916591
;; 348883142916593
;; 348883142916595
;; 348883142916597
;; 348883142916599
;; 348883142916601
;; 348883142916603
;; 348883142916605
;; 348883142916607
;; 348883142916609
;; 348883142916611
;; 348883142916613 *** 1893341
;; 348883142916615
;; 348883142916617
;; 348883142916619
;; 348883142916621
;; 348883142916623
;; 348883142916625
;; 348883142916627
;; 348883142916629
;; 348883142916631
;; 348883142916633
;; 348883142916635
;; 348883142916637
;; 348883142916639
;; 348883142916641
;; 348883142916643
;; 348883142916645
;; 348883142916647
;; 348883142916649
;; 348883142916651
;; 348883142916653
;; 348883142916655
;; 348883142916657
;; 348883142916659
;; 348883142916661
;; 348883142916663
;; 348883142916665
;; 348883142916667
;; 348883142916669
;; 348883142916671
;; 348883142916673
;; 348883142916675
;; 348883142916677
;; 348883142916679
;; 348883142916681
;; 348883142916683
;; 348883142916685
;; 348883142916687
;; 348883142916689
;; 348883142916691
;; 348883142916693
;; 348883142916695
;; 348883142916697
;; 348883142916699
;; 348883142916701
;; 348883142916703
;; 348883142916705
;; 348883142916707
;; 348883142916709
;; 348883142916711
;; 348883142916713
;; 348883142916715
;; 348883142916717
;; 348883142916719
;; 348883142916721
;; 348883142916723
;; 348883142916725
;; 348883142916727
;; 348883142916729
;; 348883142916731
;; 348883142916733
;; 348883142916735
;; 348883142916737
;; 348883142916739 *** 1809663(* 701102 (sqrt 10)) = 2217079.192099371. With 348883142916533 we took 2027795, so the prediction is roughly correct.
Let us now test whether the number we find after (* 10 348883142916530) and those after (* 10 10 348883142916530) fulfill the prediction too.
3488831429165323 *** 5971326
(search-for-primes 3488831429165301 3488831429165401)
;; ...
;; 3488831429165323 *** 5971326
;; ...(search-for-primes 34888314291653011 34888314291653511)
;; ...
;; 34888314291653021 *** 16052655
;; ...(* 5971326 (sqrt 10)) 18882990.81138261. Again, the prediction seems roughly correct.
The
smallest-divisorprocedure shown at the start of this section does lots of needless testing: After it checks to see if the number is divisible by 2 there is no point in checking to see if it is divisible by any larger even numbers. This suggests that the values used fortest-divisorshould not be 2, 3, 4, 5, 6, …, but rather 2, 3, 5, 7, 9, …. To implement this change, define a procedure next that returns 3 if its input is equal to 2 and otherwise returns its input plus 2. Modify thesmallest-divisorprocedure to use(next test-divisor)instead of(+ test-divisor 1). Withtimed-prime-testincorporating this modified version ofsmallest-divisor, run the test for each of the 12 primes found in Exercise 1.22. Since this modification halves the number of test steps, you should expect it to run about twice as fast. Is this expectation confirmed? If not, what is the observed ratio of the speeds of the two algorithms, and how do you explain the fact that it is different from 2?
Answer:
(define (smallest-divisor-mod n)
(find-divisor-mod n 2))
(define (find-divisor-mod n test-divisor)
(cond ((> (square test-divisor) n)
n)
((divides? test-divisor n)
test-divisor)
(else (find-divisor
n
(next test-divisor)))))
;; ...
(define (next n)
(if (= n 2)
3
(+ n 1)))
(define (prime?-mod n)
(= n (smallest-divisor-mod n)))
(define (timed-prime-test-mod n)
(newline)
(display n)
(start-prime-test n (runtime)))
(define (start-prime-test-mod n start-time)
(if (prime?-mod n)
(report-prime (- (runtime)
start-time))))I haven’t observed any relevant difference with the numbers I have tested. I’m not sure why that is so. One possible explanation is that the numbers I have tested are too small. Another possible explanation is that Racket performs some optimizations.
- check fn 46
Simpson’s Rule is a more accurate method of numerical integration than the method illustrated above. Using Simpson’s Rule, the integral of a function
$f$ between a and b is approximated as$\frac{h}{3} (y_0 + 4y_1 + 2y_2 + 4y_3 + 2y_4 + … + 2yn-2 + 2yn-1 + y_n)$,
where
$h = (b - a) / n$ , for some even integer$n$ , and$y_k = f(a + kh)$ . (Increasing$n$ increases the accuracy of the approximation.) Define a procedure that takes as arguments$f$ ,$a$ ,$b$ , and$n$ and returns the value of the integral, computed using Simpson’s Rule. Use your procedure to integratecubebetween 0 and 1 (with$n = 100$ and$n = 1000$ ), and compare the results to those of theintegralprocedure shown above.
Answer:
(define (integral f a b n)
(define (next x)
(if (x is odd)
(...)
(...)))
(* (/ (/ (- b a ) n) 3)
(+ y0
(sum ...)
yn)))#lang sicp
(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))
(define (cube x) (* x x x))
(define (integral f a b n)
(define (f-mod) ;;<== takes not arg?!
(define (f2 x)
(* 2 (f x)))
(define (f4 x)
(* 4 (f x)))
(if (= (remainder a 2) 0)
f2
f4))
(define (next x)
(+ x
1
(* (+ x 1)
(/ (- b a ) n))))
(* (/ (/ (- b a ) n) 3)
(+ (f 0)
(sum f-mod
(+ (+ 1 a)
(* (+ 1 a)
(/ (- b a ) n)))
next
b)
(f (+ n
(* n
(/ (- b a ) n)))))))
(define (integral-first f a b dx)
(define (add-dx x) (+ x dx))
(* (sum f (+ a (/ dx 2.0)) add-dx b)
dx))#lang sicp
(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))
(define (cube x) (* x x x))
(define (integral f a b n)
(define (f-mod x)
(define (f2 x)
(* 2 (f x)))
(define (f4 x)
(* 4 (f x)))
(cond ((= x 0) (f x))
((= x n) (f x))
((= (remainder (- x a) 2) 0) (f2 x))
(else (f4 x))))
(define (next x)
(+ x
1
(* (+ x 1) (/ (- b a) n))))
(* (/ (/ (- b a) n) 3)
(sum f-mod a next b)
n))
;;(integral cube 0 1 1000) ; ==> 0 :(#lang sicp
(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))
(define (cube x) (* x x x))
(define (integral f a b n)
(define (f-mod x)
(define (f2 x)
(* 2 (f x)))
(define (f4 x)
(* 4 (f x)))
(cond ((= x 0) (f x))
((= x n) (f x))
((= (remainder (- x a) 2) 0) (f2 x))
(else (f4 x))))
(define (next x)
(+ x 1))
(* (/ (/ (- b a) n) 3)
(sum f-mod (* a (/ (- b a) n)) next b)
n))
(integral cube 0 1 1000) ;; 1*1/3 :(#lang sicp
(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))
(define (cube x) (* x x x))
(define (integral f a b n)
(define (f-mod x)
(define (f2 x)
(* 2 (f x)))
(define (f4 x)
(* 4 (f x)))
(cond ((= x a) (f x))
((= (- (/ x (/ (- b a) n)) a) n) (f x))
((= (remainder (- (/ x (/ (- b a) n)) a) 2) 0) (f2 x))
(else (f4 x))))
(define (next x)
(+ x
(/ (- b a) n)))
(* (/ (/ (- b a) n) 3)
(sum f-mod
a
next
(+ a (* n (/ (- b a) n))))))
(integral cube 0 1 100);; 1/4 :)Exercise:
The sum procedure above generates a linear recursion. The procedure can be rewritten so that the sum is performed iteratively. Show how to do this by filling in the missing expressions in the following definition:
(define (sum term a next b) (define (iter a result) (if ⟨??⟩ ⟨??⟩ (iter ⟨??⟩ ⟨??⟩))) (iter ⟨??⟩ ⟨??⟩))
Answer:
(define (sum term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (+ (term a) result))))
(iter a 0))Exercise:
- The sum procedure is only the simplest of a vast number of similar abstractions that can be captured as higher-order procedures.[fn: The intent of Exercise 1.31 through Exercise 1.33 is to demonstrate the expressive power that is attained by using an appropriate abstraction to consolidate many seemingly disparate operations. However, though accumulation and filtering are elegant ideas, our hands are somewhat tied in using them at this point since we do not yet have data structures to provide suitable means of combination for these abstractions. We will return to these ideas in 2.2.3 when we show how to use sequences as interfaces for combining filters and accumulators to build even more powerful abstractions. We will see there how these methods really come into their own as a powerful and elegant approach to designing programs.] Write an analogous procedure called product that returns the product of the values of a function at points over a given range. Show how to define factorial in terms of product. Also use product to compute approximations to π using the formula…
$\frac{π}{4} = \frac{2 ⋅ 4 ⋅ 4 ⋅ 6 ⋅ 6 ⋅ 8 ⋅ …}{3 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 7 ⋅ 7 ⋅ …}$ - If your product procedure generates a recursive process, write one that generates an iterative process. If it generates an iterative process, write one that generates a recursive process.
Answer:
Here is product.
(define (product term a next b)
(if (> a b)
1
(* (term a) (product term (next a) next b))))Here is factorial defined in terms of product.
(define (factorial n)
(define (inc x) (+ 1 x))
(define (indentity x) x)
(product identity 1 inc n))Here is one way of computing an approximation to
(define (product* begin end)
(define (identity x) x)
(define (inc2 x) (+ 2 x))
(product identity begin inc2 end))
(* (/ (* 2 (product* 4 8) (product* 4 6))
(square (product* 3 7)))
4.0)My product procedure generates a recursive process (product that generates an iterative
process (
(define (product term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (* (term a) result))))
(iter a 1))We can notice that we start our iteration multiplying by 1, whereas we
were ending our recursion multiplying by 1. (Analogously with sum
and 0).
- Show that
sumandproduct(Exercise 1.31) are both special cases of a still more general notion calledaccumulatethat combines a collection of terms, using some general accumulation function:(accumulate combiner null-value term a next b)
Accumulatetakes as arguments the same term and range specifications assumandproduct, together with acombinerprocedure (of two arguments) that specifies how the current term is to be combined with the accumulation of the preceding terms and a null-value that specifies what base value to use when the terms run out. Write accumulate and show how sum and product can both be defined as simple calls to accumulate.- If your accumulate procedure generates a recursive process, write one that generates an iterative process. If it generates an iterative process, write one that generates a recursive process.
Answer:
By looking at the recursive version of sum and product, we can
observe that only certain elements in the two bodies are
different. They are:
- The first expression after the if;
- The procedure applied in the tail call;
As far as I can tentatively see, this means that the concepts
expressed sum and product belong to a more general concept.
This latter concept abstracts over the two parts of the body mentioned. The first abstraction is an abstraction over a numeric value. The second abstraction is an abstraction over a procedure.
This more general concept can itself be expressed by a procedure definition
(define (accumulate combiner null-value term a next b)
(if (> a b)
null-value
(combiner (term a)
(accumulate combiner null-value term (next a) next b))))(sum identity 1 inc 5) ;; => 15
(accumulate + 0 identity 1 inc 5) ;; => 15
(product identity 2 inc 9) ;; => 362880
(accumulate * 1 identity 2 inc 9) ;; => 362880My accumulate generate a recursive process. Here is an iterative version:
(define (accumulate combiner null-value term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (combiner (term a) result))))
(iter a null-value))Exercise:
You can obtain an even more general version of
accumulate(Exercise 1.32) by introducing the notion of afilteron the terms to be combined. That is, combine only those terms derived from values in the range that satisfy a specified condition. The resultingfiltered-accumulateabstraction takes the same arguments as accumulate, together with an additional predicate of one argument that specifies the filter. Writefiltered-accumulateas a procedure. Show how to express the following usingfiltered-accumulate:
- the sum of the squares of the prime numbers in the interval
atob(assuming that you have aprime?predicate already written)- the product of all the positive integers less than
$n$ that are relatively prime to $n$j (i.e., all positive integers$i < n$ such that$GCD(i,n)=1$ ).
Answer:
(define (filtered-accumulate combiner filter null-value term a next b)
(cond ((> a b) null-value)
((filter a) (combiner (term a)
(filtered-accumulate combiner filter null-value term (next a) next b)))
(else (filtered-accumulate combiner filter null-value term (next a) next b))))(define (sum-of-the-squares-of-primes a b)
(filtered-accumulate + prime? 0 square a inc2 b))(define (product-int-less-than-rel-prime-to n)
(define (rel-prime-to-n x)
(= (gcd x n)
1))
(filtered-accumulate * rel-prime-to-n 1 1 inc1 (- n 1)))Suppose we define the procedure
(define (f g) (g 2))Then we have
(f square) 4 (f (lambda (z) (* z (+ z 1)))) 6What happens if we (perversely) ask the interpreter to evaluate the combination (f f)? Explain?
Answer:
According to the substitution model:
(f f) (f 2) (2 2)
In `(2 2)`, `2` is used as if it denoted a procedure. But `2` does not denote a procedure. `2` denotes a number. So, I predict that the interpreter will complain about this.
In fact, when trying to evaluate the combination, DrRacket says:
application: not a procedures; expected a procedures that can be applied to arguments given: 2
Define a procedure double that takes a procedure of one argument as argument and returns a procedure that applies the original procedure twice. For example, if
incis a procedure that adds 1 to its argument, then(double inc)should be a procedure that adds 2. What value is returned by(((double (double double)) inc) 5)
Answer:
;; (((double (double double)) inc) 5)
;; (double inc) => (lambda (x) (inc (inc x)))
;; (double double) => (lambda (x) (double (double x)))
;; (double (double double)) =>
;; (lambda (x) ((lambda (x) (double (double x)))
;; ((lambda (x) (double (double x))) x)))
;; so:
((double (double double) inc))
;; =>
((lambda (x) (double (double x)))
(double (double inc)))
;; =>
((lambda (x) (double (double x)))
(double (lambda (x) (inc (inc x)))))
;; =>
((lambda (x) (double (double x)))
(lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))))
;; =>
(double (double (lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))))
;; =>
(double (lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x))))
;; =>
(lambda (x) ((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
x)))
;; now let's apply that lambda to 5:
((lambda (x) ((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
x))) 5)
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
5))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) 5)))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) 5))))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) (inc (inc x)))
(inc (inc 5)))))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) (inc (inc x)))
(inc 6))))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) (inc (inc x)))
7)))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
(inc (inc 7))))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
(inc 8)))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
9))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) 9)))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) (inc (inc x)))
(inc (inc 9))))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) (inc (inc x)))
(inc 10)))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
((lambda (x) (inc (inc x)))
11))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
(inc (inc 11)))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
(inc 12))
;; =>
((lambda (x)
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) x)))
13)
;; =>
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x))) 13))
;; =>
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) 13)))
;; =>
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) (inc (inc x)))
(inc (inc 13))))
;; =>
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) (inc (inc x)))
(inc 14)))
;; =>
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
((lambda (x) (inc (inc x)))
15))
;; =>
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
(inc (inc 15)))
;; =>
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
(inc 16))
;; =>
((lambda (x) ((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) x)))
17)
;; =>
((lambda (x) (inc (inc x)))
((lambda (x) (inc (inc x))) 17))
;; =>
((lambda (x) (inc (inc x)))
(inc (inc 17)))
;; =>
((lambda (x) (inc (inc x)))
(inc 18))
;; =>
((lambda (x) (inc (inc x)))
19)
;; =>
(inc (inc 19))
;; =>
(inc 20)
;; =>
21
Exercise:
Let
$f$ and$g$ be two one-argument functions. The composition$f$ after$g$ is defined to be the function$x \mapsto f(g(x))$ . Define a procedurecomposethat implements composition. For example, ifincis a procedure that adds 1 to its argument,((compose square inc) 6) 49
Answer:
(define (compose f1 f2)
(lambda (x) (f1 (f2 x))))Exercise:
If
$f$ is a numerical function and$n$ is a positive integer, then we can form the $nth$ repeated application of$f$ , which is defined to be the function whose value at$x$ is$f(f(…(f(x))…))$ . For example, if$f$ is the function$x \mapsto x+1$ , then the $nth$ repeated application of$f$ is the function$x \mapsto x+n$ . If$f$ is the operation of squaring a number, then the $nth$ repeated application of$f$ is the function that raises its argument to the $2n$ -th power. Write a procedure that takes as inputs a procedure that computes$f$ and a positive integer$n$ and returns the procedure that computes the $nth$ repeated application of$f$ . Your procedure should be able to be used as follows:((repeated square 2) 5) 625Hint: You may find it convenient to use
composefrom Exercise 1.42.
Answer:
(define (repeated f n)
(cond ((= x 1) f)
((= x 2) (compose f f))
(else (compose f (repeatedly-apply f (- n 1))))))(define (smooth f)
(lambda (x)
(/ 3
(+ (f (- x 0.01))
(f x)
(f (+ x 0.01))))))
(define (10th-smoothed-f f)
((repeated smooth 10) f))Several of the numerical methods described in this chapter are instances of an extremely general computational strategy known as iterative improvement. Iterative improvement says that, to compute something, we start with an initial guess for the answer, test if the guess is good enough, and otherwise improve the guess and continue the process using the improved guess as the new guess. Write a procedure
iterative-improvethat takes two procedures as arguments: a method for telling whether a guess is good enough and a method for improving a guess.Iterative-improveshould return as its value a procedure that takes a guess as argument and keeps improving the guess until it is good enough. Rewrite the sqrt procedure of 1.1.7 and the fixed-point procedure of 1.3.3 in terms of iterative-improve.
Answer:
(define (iterative-improve good-enough? improve)
(define (iterative-improve-inner guess)
(if (good-enough? guess) guess
(iterative-improve-inner (improve guess))))
(lambda (x) (iterative-improve-inner x)))(define (sqrt x)
((iterative-improve (lambda (guess)
(< (abs (- (square guess) x)) 0.001))
(lambda (guess)
(average guess (/ x guess))))
1.0))List of the exercises I have skipped:
- 1.13.
- 1.19.
- 1.24. (It should be fairly easy).
- 1.25.
- 1.26.
- 1.27.
- 1.28.
- 1.35
- 1.36
- 1.37
- 1.38
- 1.39
- 1.45
Exercise:
Define a better version of make-rat that handles both positive and negative arguments. Make-rat should normalize the sign so that if the rational number is positive, both the numerator and denominator are positive, and if the rational number is negative, only the numerator is negative.
Answer:
(define (make-rat n d)
(let ((g (gcd n d)))
(if (or (and (> n 0) (> d 0))
(and (< n 0) (< d 0)))
(cons (/ (abs n) (abs g))
(/ (abs d) (abs g)))
(cons (- (/ (abs n) (abs g)))
(/ (abs d) (abs g))))))
(print-rat (make-rat 2 4)) ;; => 1/2
(print-rat (make-rat -2 4)) ;; => -1/2
(print-rat (make-rat 2 -4)) ;; => -1/2Consider the problem of representing line segments in a plane. Each segment is represented as a pair of points: a starting point and an ending point. Define a constructor
make-segmentand selectorsstart-segmentandend-segmentthat define the representation of segments in terms of points. Furthermore, a point can be represented as a pair of numbers: the$x$ coordinate and the$y$ coordinate. Accordingly, specify a constructormake-pointand selectorsx-pointandy-pointthat define this representation. Finally, using your selectors and constructors, define a proceduremidpoint-segmentthat takes a line segment as argument and returns its midpoint (the point whose coordinates are the average of the coordinates of the endpoints). To try your procedures, you’ll need a way to print points:(define (print-point p) (newline) (display "(") (display (x-point p)) (display ",") (display (y-point p)) (display ")"))
Answer:
;; constructor
(define (make-segment s e) (cons s e))
;; selectors
(define (start-segment x) (car x))
(define (end-segment x) (cdr x))
;; constructor
(define (make-point x y) (cons x y))
;; selectors
(define (x-point x) (car x))
(define (y-point x) (cdr x))
(define (mid-point-segment line)
(make-point (/ (+ (x-point (start-segment line))
(x-point (end-segment line)))
2)
(/ (+ (y-point (start-segment line))
(y-point (end-segment line)))
2)))
(define (print-point p)
(newline)
(display "(")
(display (x-point p))
(display ",")
(display (y-point p))
(display ")"))
(print-point (mid-point-segment (make-segment (make-point 2 2) (make-point 6 4))))Exercise:
Implement a representation for rectangles in a plane. (Hint: You may want to make use of Exercise 2.2.) In terms of your constructors and selectors, create procedures that compute the perimeter and the area of a given rectangle. Now implement a different representation for rectangles. Can you design your system with suitable abstraction barriers, so that the same perimeter and area procedures will work using either representation?
Answer:
I’m assuming the sides of the rectangle and the axes are parallel.
Sides are represented by segments whose points whose order is clockwise, E.g., left-side: (bottom-point . top-point), top-side: (left-point . right-point).
1st representation:
(define (make-rec left-side top-side)
(cons left top))
(define (length rec)
(let ((top-left-point (cdr (car rec)))
(top-right-point (car (cdr rec))))
(abs (- (x-point top-right-point)
(x-point top-left-point)))))
(define (width rec)
(let ((bottom-left-point (car (car rec)))
(top-left-point (cdr (car rec))))
(abs (- (y-point top-left-point)
(y-point bottom-left-point)))))2nd representation:
(define (make-rec right-side bottom-side)
(cons right-side bottom-side))
(define (length rec)
(let ((bottom-left-point (cdr (cdr rec)))
(bottom-right-point (car (cdr rec))))
(abs (- (x-point bottom-right-point)
(x-point bottom-left-point)))))
(define (width rec)
(let ((top-right-point (car (car rec)))
(bottom-right-point (car (cdr rec))))
(abs (- (y-point top-right-point)
(y-point bottom-right-point)))))- Procedures which work with both representations:
(define (perimeter rec) (* 2 (+ (length rec) (width rec)))) (define (area rec) (* (length rec) (width rec)))
Exercise:
Here is an alternative procedural representation of pairs. For this representation, verify that (car (cons x y)) yields x for any objects x and y.
(define (cons x y) (lambda (m) (m x y))) (define (car z) (z (lambda (p q) p)))What is the corresponding definition of cdr? (Hint: To verify that this works, make use of the substitution model of 1.1.5.)
Answer:
(car (cons x y)) is the application car to the result of the
application of cons to x and y.
The application of cons to x and y is (lambda (m) (m x y)).
So, the application of car to the application of cons to x and y
is (car (lambda (m) (m x y))).
We can now take the body of car and replace each istance of z with
(car (lambda (m) (m x y))). This gives us:
((lambda (m) (m x y)) (lambda (p q) p))This latter combination is the application of (lambda (m) (m x y))
to (lambda (p q) p).
We can now take the body of the first lambda (the procedure we are
applying) and replace each instance of m with the second lambda
(that to which we are applying the first lambda). This gives us:
((lambda (p q) p) x y)This latter combination is the application of (lambda (p q) p) to
x and y. Which evaluates to x.
The corresponding definition of cdr is:
(define (cdr z)
(z (lambda (p q) q)))Show that we can represent pairs of nonnegative integers using only numbers and arithmetic operations if we represent the pair
$a$ and$b$ as the integer that is the produce of$2^a3^b$ . Give the corresponding definitions of the procedurescons,car, andcdr.
;; from chapter 1 ******
(define (square x) (* x x))
(define (fast-expt b n)
(cond ((= n 0)
1)
((even? n)
(square (fast-expt b (/ n 2))))
(else
(* b (fast-expt b (- n 1))))))
(define (even? n)
(= (remainder n 2) 0))
;; *********************
(define (cons a b)
(* (fast-expt 2 a)
(fast-expt 3 b)))
(define (car x)
(define (car-iter x i)
(if (not (even? x))
i
(car-iter (/ x 2) (+ i 1))))
(car-iter x 0))
(define (cdr x)
(define (cdr-iter x i)
(if (not (= (remainder x 3) 0))
i
(cdr-iter (/ x 3) (+ i 1))))
(cdr-iter x 0))
(define my-pair (cons 3 2)) ;; my-pair is now 72
(car my-pair) ;; => 3
(cdr my-pair) ;; => 2
(cons 7 5)
(define another-pair (cons 7 5)) ;; another-pair is now 31104
(car another-pair) ;; => 7
(cdr another-pair) ;; => 5Exercise:
In case representing pairs as procedures wasn’t mind-boggling enough, consider that, in a language that can manipulate procedures, we can get by without numbers (at least insofar as nonnegative integers are concerned) by implementing 0 and the operation of adding 1 as
(define zero (lambda (f) (lambda (x) x))) (define (add-1 n) (lambda (f) (lambda (x) (f ((n f) x)))))This representation is known as Church numerals, after its inventor, Alonzo Church, the logician who invented the λ-calculus.
Define one and
twodirectly (not in terms ofzeroandadd-1). (Hint: Use substitution to evaluate(add-1 zero)). Give a direct definition of the addition procedure+(not in terms of repeated application ofadd-1).
Answer:
(define zero (lambda (f) (lambda (x) x)))
(define (zero-b f) (lambda (x) x))
(define (add-1 n)
(lambda (f) (lambda (x) (f ((n f) x)))))
(add-1 zero)
(lambda (f)
(lambda (x)
(f
(((lambda (f)
(lambda (x) x))
f)
x))))
;; =>
(lambda (f)
(lambda (x)
(f
((lambda (x) x)
x))))
;; => the following should be the def. of 1
(lambda (f)
(lambda (x)
(f x)))
;; this above should be 1
;; So:
(define one
(lambda (f)
(lambda (x)
(f x))))
;; let's try to apply add-1 to what we think is 1
(lambda (f)
(lambda (x)
(f
(((lambda (f)
(lambda (x)
(f x))) f)
x))))
;; =>
(lambda (f)
(lambda (x)
(f
((lambda (x) (f x)) x))))
;; =>
(lambda (f)
(lambda (x)
(f (f x))))
;; this one above should be 2.
;; So:
(define two
(lambda (f)
(lambda (x)
(f (f x)))))Addition:
(define add (lambda (n1)
(lambda (n2)
(lambda (f)
(lambda (x)
((n2 f) ((n1 f) x)))))))
;; or
(define (add n1 n2)
(lambda (f)
(lambda (x)
((n2 f) ((n1 f) x)))))
;; lets try add 1 and 1
;; 1 is (lambda (f) (lambda (x) (f x)))
(lambda (f)
(lambda (x)
(((lambda (f) (lambda (x) (f x))) f) (((lambda (f) (lambda (x) (f x))) f) x))))
(lambda (f)
(lambda (x)
((lambda (x) (f x)) (((lambda (f) (lambda (x) (f x))) f) x))))
(lambda (f)
(lambda (x)
((lambda (x) (f x)) ((lambda (x) (f x)) x))))
(lambda (f)
(lambda (x)
((lambda (x) (f x)) (f x))))
(lambda (f)
(lambda (x)
((lambda (x) (f x)) (f x))))
(lambda (f)
(lambda (x)
((f (f x)))))
;; lets try add 1 and 2
;; 1 is (lambda (f) (lambda (x) (f x)))
;; 2 is (lambda (f) (lambda (x) (f (f x))))
(lambda (f)
(lambda (x)
(((lambda (f) (lambda (x) (f x))) f) (((lambda (f) (lambda (x) (f (f x)))) f) x))))
;; it seems to work...
(lambda (f)
(lambda (x)
((f (f (f x))))))
(define (lower-bound x) (car x))
(define (upper-bound x) (cdr x))Answer:
Following Alyssa’s way of reasoning, we should determine what’s the
minimum value the subtraction could be, and let that value be the
lower bound (the first argument of make-interval). And we should
determine what’s the maximum value the subtraction could be, and let
that value be the upper bound (the second argument of
make-interval).
The minimum value the subtraction could be is the result of subtracting the upper bound of y to the lower bound of x.
The maximum value the subtraction could be is the result of subtracting the lower bound of y to the upper bound of x.
So:
(define (sub-interval x y)
(make-interval (- (lower-bound x) (upper-bound y))
(- (upper-bound x) (lower-bound y))))Exercise:
The width of an interval is half of the difference between its upper and lower bounds. The width is a measure of the uncertainty of the number specified by the interval. For some arithmetic operations the width of the result of combining two intervals is a function only of the widths of the argument intervals, whereas for others the width of the combination is not a function of the widths of the argument intervals. Show that the width of the sum (or difference) of two intervals is a function only of the widths of the intervals being added (or subtracted). Give examples to show that this is not true for multiplication or division.
Answer:
Let’s take the interval (make-interval 1 2) and the interval
(make-interval 3 4). The width of both is
Given this observation, we can hypothesize that the width of the sum of two intervals is the sum of the widths of the two intervals being added.
Let’s make another observation to see whether it is compatible with
this hypothesis. Let’s consider the interval (make-interval 3 6) and
the interval (make-interval 5 9). The width of the former is
Let’s try to somehow prove that it is generally the case that the width of the sum of two intervals is the sum of the widths of the two intervals being added.
##############sketchy###################
- The width of an interval is the the difference between upper bound and lower bound divided by 2.
- We can just focus on the difference, disregarding the division for simplicity.
- The sum of two interval a and b will have a difference which is the sum of the differences of the two intervals. (because…)
- But, if so, then the sum of the widths of a and b = the width of the sum.
- Therefore, the width of the sum is a function of the width of the two intervals.
########################################
Example of how this is not true for multiplication.
(make-interval 2 4) has a width of 1. (make-interval 3 5) has a width
of 1 too. Their multiplication gives an interval whose lower bound is
If the width of the multiplication of two interval were a function of only the widths of the interval being multiplied, then the width of any other multiplication of two intervals whose widths are, respectively, 1 and 1, must be 7.
We expect this hypothesis to be falsified.
To try to falsify it, let’s consider the two intervals (make-interval
6 8) and (make-interval 10 12). The width of both is
We have computed the width of the multiplication of two intervals
whose width was respectively
Exercise:
Ben Bitdiddle, an expert systems programmer, looks over Alyssa’s shoulder and comments that it is not clear what it means to divide by an interval that spans zero. Modify Alyssa’s code to check for this condition and to signal an error if it occurs.
Answer:
(define (div-interval x y)
(if (= (lower-bound y) (upper-bound y))
(display "error")
(mul-interval x
(make-interval
(/ 1.0 (upper-bound y))
(/ 1.0 (lower-bound y))))))Exercise:
In passing, Ben also cryptically comments: “By testing the signs of the endpoints of the intervals, it is possible to break mul-interval into nine cases, only one of which requires more than two multiplications.” Rewrite this procedure using Ben’s suggestion.
After debugging her program, Alyssa shows it to a potential user, who complains that her program solves the wrong problem. He wants a program that can deal with numbers represented as a center value and an additive tolerance; for example, he wants to work with intervals such as 3.5 ± 0.15 rather than [3.35, 3.65]. Alyssa returns to her desk and fixes this problem by supplying an alternate constructor and alternate selectors:
(define (make-center-width c w) (make-interval (- c w) (+ c w))) (define (center i) (/ (+ (lower-bound i) (upper-bound i)) 2)) (define (width i) (/ (- (upper-bound i) (lower-bound i)) 2))Unfortunately, most of Alyssa’s users are engineers. Real engineering situations usually involve measurements with only a small uncertainty, measured as the ratio of the width of the interval to the midpoint of the interval. Engineers usually specify percentage tolerances on the parameters of devices, as in the resistor specifications given earlier.
Answer:
Cons is used to “glue“ two things together into a pair. This
allows us to construct compound data.
We can represent a pair using the so-called box-and-pointer notation, in which each object is represented as a pointer to a box (the box for a pair is actually a double box):
*Figure 2.2:* Box-and-pointer representation of `(cons 1 2)'.
+---+---+ +---+
---->| * | *-+---->| 2 |
+-|-+---+ +---+
|
V
+---+
| 1 |
+---+
[Figure from SICP Unofficial Texinfo Format version 2.neilvandyke4 (January 10, 2007)]
We have already seen that cons can be used to combine not only numbers but pairs as well. […] As a consequence, pairs provide a universal building block from which we can construct all sorts of data structures.
The authors refer to the ability to create pairs whose elements are pairs as the closure property of cons, borrowing the term from abstract algebra.
Closure is the key to power in any means of combination because it permits us to create hierarchical structures — structures made up of parts, which themselves are made up of parts, and so on.
There are many ways to represent a sequence (an ordered collection of data objects) using pairs. Here is one:
(cons 1
(cons 2
(cons 3
(cons 4 nil))))A sequence of pairs, formed by nested conses, like that above, is
called list. Scheme provide the primitive list to create such
sequences.
(list <a_1> <a_2> ... <a_n>)is equivalent to
(cons ⟨a_1⟩
(cons ⟨a_2⟩
(cons ...
(cons ⟨a_n⟩
nil)...)))Do not confuse the expression (list 1 2 3 4) with the list (1 2 3
4)…
car… cdr… cadr…
nil can be thought of as a sequence with no elements, the empty
list.
List operations (Two conventional programming techniques: “cdring down” and “consing up”).
length:
Recursively:
(define (length items)
(if (null? items)
0
(+ 1 (length (cdr items)))))Iteratively:
(define (length items)
(define (length-iter a count)
(if (null? a)
count
(length-iter (cdr a) (+ 1 count))))
(length-iter items 0))list-ref:
(define (list-ref items n)
(if (= n 0)
(car items)
(list-ref (cdr items)
(- n 1))))append:
(define (append list1 list2)
(if (null? list1)
list2
(cons (car list1)
(append (cdr list1)
list2))))Exercise:
Define a procedure last-pair that returns the list that contains only the last element of a given (nonempty) list:
(last-pair (list 23 72 149 34)) (34)
Answer:
(define (last-pair l)
(if (null? (cdr l))
l
(last-pair (cdr l))))Exercise:
Define a procedure `reverse’ that takes a list as argument and returns a list of the same elements in reverse order:
(reverse (list 1 4 9 16 25)) (25 16 9 4 1)
Answer:
My intuitive solution was interative:
(define (reverse l)
(define (reverse-iter l result)
(if (null? l)
result
(reverse-iter (cdr l) (cons (car l) result))))
(reverse-iter l (list)))After having solved the exercise iteratively, I’ve looked for a recursive solution on the web and I found this one:
(define (reverse l)
(if (null? l)
nil
(append (reverse (cdr l))
(list (car l)))));; iterative solution (three slightly different versions):
(define (same-parity1 i . rest)
(define (condition i1 i2)
(= (remainder i1 2)
(remainder i2 2)))
(define (same-party-inner i l result)
(if (null? l)
result
(same-party-inner i
(cdr l)
(if (condition i (car l))
(cons (car l) result)
result))))
(cons i (reverse (same-party-inner i rest (list)))))
(define (same-parity2 i . rest)
(define (condition i1 i2)
(= (remainder i1 2)
(remainder i2 2)))
(define (same-party-inner i l result)
(if (null? l)
result
(same-party-inner i
(cdr l)
(if (condition i (car l))
(cons (car l) result)
result))))
(reverse (same-party-inner i rest (list i))))
(define (same-parity3 i . rest)
(define (condition i1 i2)
(= (remainder i1 2)
(remainder i2 2)))
(define (same-party-inner i l result)
(if (null? l)
result
(same-party-inner i
(cdr l)
(if (condition i (car l))
(append result (list (car l)))
result))))
(same-party-inner i rest (list i)))
(same-parity1 1 2 3 4 5 6 7) ;; (1 3 5 7)
(same-parity2 1 2 3 4 5 6 7) ;; (1 3 5 7)
(same-parity3 1 2 3 4 5 6 7) ;; (1 3 5 7)
(define (square-list items)
(if (null? items)
nil
(cons (square (car items))
(square-list (cdr items)))))
(define (square-list items)
(map square items))“…defining square-list this way produces the answer list in the reverse order of the one desired. Why?”
That procedures conses the square of first element of the list `items` onto the empty list, obtaining foo0, the list that contains the square of first element of the list `items`. Then, it conses the square of the second element of the list `items` onto foo0, obtaining foo1, the list that that contains the square of second element of the list `items` and the square of first element of the list `items`, in that order. Then it conses the square of the third element onto foo1, obtaing foo2, the list that that contains the square of third element of the list `items`, the square of second element of the list `items` and the square of first element of the list `items`, in that order. etc.
“This doesn’t work either. Explain.”
That procedures conses nil into the first element of `items`, obtaining foo0, the pair whose first elemetn is nil and the second element is the first element of `items. Then, it conses foo0 into the second element of `items`, obtaining foo1, the pair whose first element is foo0 and second element is the second element of `items`. Then it conses foo1 onto the third element of `items`…
(define (for-each proc items)
(if (null? items)
true
(and (proc (car items))
(for-each proc (cdr items)))))(define (count-leaves x)
(con ((null? x) 0)
((not (pair? x)) 1)
(+ (count-leaves (car x))
(count-leaves (cdr x)))))see notebook
(setq x '(1 3 (5 7) 9))
(car (cdr (car (cdr (cdr x))))) ;; => 7
(setq x '((7)))
(car (car x)) ;; => 7
(setq x '(1 (2 (3 (4 (5 (6 7)))))))
(car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr x)))))))))))) ;; => 7;; (append x y) => (1 2 3 4 5 6)
;; (cons x y) => ((1 2 3) 4 5 6)
;; (list x y) => ((1 2 3) (4 5 6))(define (deep-reverse x)
(define (iter x result)
(cond ((null? x) result)
((not (pair? x)) x)
(else (iter (cdr x)
(cons (iter (car x) nil) result))))) (iter x nil));; I've read The Little Schemer a while ago, in which a function atom?
;; like this one is defined:
(define (atom? x)
(and (not (pair? x)) (not (null? x))))
(define (deep-reverse x)
(define (iter x result)
(cond ((atom? x) x)
((null? x) result)
(else (iter (cdr x)
(cons (iter (car x) nil) result))))) (iter x nil))(defun iter (x result)
(cond ((not (listp x)) x)
((null x) result)
(t (iter (cdr x)
(cons (iter (car x) nil) result)))))
(defun deep-reverse (x)
(iter x nil))
(deep-reverse '(1 2 3 (4 5)))
;; => ((5 4) 3 2 1)Recursive-process-evolving version:
;; first attempt...
;; (define (deep-r t)
;; (cond ((null? t) nil)
;; ((pair? t) (append (deep-r (cdr t))
;; (deep-r (car t))))
;; (else (list t))))
(define (deep-reverse t)
(cond ((null? t) nil)
((pair? t) (append (list (deep-reverse (cdr t)))
(list (deep-reverse (car t)))))
(else (list t))))Exercise:
Write a procedure fringe that takes as argument a tree (represented as a list) and returns a list whose elements are all the leaves of the tree arranged in left-to-right order. For example,
(define x (list (list 1 2) (list 3 4))) (fringe x) (1 2 3 4) (fringe (list x x)) (1 2 3 4 1 2 3 4)
Answer:
(define (fringe x)
(cond ((null? x) nil)
((not (pair? x)) (list x))
(else (append (fringe (car x))
(fringe (cdr x))))))(define (fringe2 t)
(cond ((null? t) nil)
((pair? t) (append (fringe2 (car t))
(fringe2 (cdr t))))
(else (list t))))Exercise:
A binary mobile consists of two branches, a left branch and a right branch. Each branch is a rod of a certain length, from which hangs either a weight or another binary mobile. We can represent a binary mobile using compound data by constructing it from two branches (for example, using
list):(define (make-mobile left right) (list left right))A branch is constructed from a
length(which must be a number) together with astructure, which may be either a number (representing a simple weight) or another mobile:(define (make-branch length structure) (list length structure))
- Write the corresponding selectors
left-branchandright-branch, which return the branches of a mobile, andbranch-lengthandbranch-structure, which return the components of a branch.- Using your selectors, define a procedure
total-weightthat returns the total weight of a mobile.- A mobile is said to be balanced if the torque applied by its top-left branch is equal to that applied by its top-right branch (that is, if the length of the left rod multiplied by the weight hanging from that rod is equal to the corresponding product for the right side) and if each of the submobiles hanging off its branches is balanced. Design a predicate that tests whether a binary mobile is balanced.
- Suppose we change the representation of mobiles so that the constructors are
(define (make-mobile left right) (cons left right)) (define (make-branch length structure) (cons length structure))How much do you need to change your programs to convert to the new representation?
Answer:
1)
(define (make-mobile left right)
(list left right))
(define (make-branch length structure)
(list length structure))
(define (left-branch mobile)
(car mobile))
(define (right-branch mobile)
(car (cdr mobile)))
(define (branch-length branch)
(car branch))
(define (branch-structure branch)
(car (cdr branch)))
2)
- The total weight of a mobile is the total weight of the left branch plus the total weight of the left branch. (In this context, something is a branch if its car is a pair.)
- The total weight of branch whose branch structure is a mobile, is the the total weight of the mobile. (We can check whether a the branch structure of a mobile is a mobile by checking whether is a pair).
- The total weight of a branch whose branch structure is a weight, is the the weight.
With these three rules above we can write our function:
(define (total-weight x)
(cond ((pair? (car x)) (+ (total-weight (left-branch x))
(total-weight (right-branch x))))
((pair? (branch-structure x)) (total-weight (branch-structure x)))
((not (pair? (branch-structure x))) (branch-structure x))))(make-mobile (make-branch 1 2) (make-branch 3 4)) ;; => ((1 2) (3 4))
(left-branch (make-mobile (make-branch 1 2) (make-branch 3 4))) ;; => (1 2)
(right-branch (make-mobile (make-branch 1 2) (make-branch 3 4))) ;; => (3 4)
(branch-structure (right-branch (make-mobile (make-branch 1 2) (make-branch 3 4)))) ;; => 4
(total-weight (make-mobile (make-branch 1 2) (make-branch 3 4))) ;; => 6
(total-weight (make-mobile (make-branch 1 2) (make-mobile (make-branch 1 2) (make-branch 3 4)))) ;; => 8
(total-weight (make-mobile (make-mobile (make-branch 1 2) (make-branch 3 4)) (make-mobile (make-branch 1 2) (make-branch 3 4)))) ;; => 123)
(define (torque branch)
(* (branch-length branch)
(total-weight branch)))
(define (isBalanced mobile)
(cond ((not (pair? (branch-structure (right-branch mobile))))
(= (torque (left-branch mobile))
(torque (right-branch mobile))))
(else (and (= (torque (left-branch mobile))
(torque (right-branch mobile)))
(isBalanced (branch-structure (right-branch mobile)))))))
(isBalanced (make-mobile (make-branch 2 2) (make-branch 2 2))) ;; => #t
(isBalanced (make-mobile (make-branch 2 2) (make-branch 2 3))) ;; => #f
(isBalanced (make-mobile (make-branch 2 2)
(make-branch 2 (make-mobile (make-branch 1 1)
(make-branch 1 1 ))))) ;; => #t
(isBalanced (make-mobile (make-branch 2 2)
(make-branch 2 (make-mobile (make-branch 2 1)
(make-branch 1 1 ))))) ;; => #f4)
If we changed the representation of mobiles so to have
(define (make-mobile left right)
(cons left right))
(define (make-branch length structure)
(cons length structure))then, we would only need to change the selectors right-branch and
branch-structure:
(define (right-branch mobile)
(cdr mobile))
(define (branch-structure branch)
(cdr branch))Both left-branch and branch-length would still work, and neither
total-weight nor isBalanced depend on the details of how mobiles
and branchs are constructed.
Define a procedure square-tree analogous to the square-list procedure of Exercise 2.21. That is, square-tree should behave as follows:
(square-tree (list 1 (list 2 (list 3 4) 5) (list 6 7))) (1 (4 (9 16) 25) (36 49))Define square-tree both directly (i.e., without using any higher-order procedures) and also by using map and recursion.
(define (square x) (* x x))
(define (square-tree tree)
(cond ((null? tree) nil)
((not (pair? tree)) (square tree))
(else (cons (square-tree (car tree))
(square-tree (cdr tree))))))
(define (square-tree tree)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(square-tree sub-tree)
(square sub-tree)))
tree))“Directly”:
(define (tree-map proc tree)
(cond ((null? tree) nil)
((not (pair? tree)) (proc tree))
(else (cons (tree-map proc (car tree))
(tree-map proc (cdr tree))))))
Using map:
(define (tree-map proc tree)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(tree-map proc sub-tree)
(proc sub-tree)))
tree))The first guess was correct:
(define (subsets s)
(if (null? s)
(list nil)
(let ((rest (subsets (cdr s))))
(append rest (map (lambda (x)
(cons (car s) x))
rest)))))Let’s have a look at the evolution of the process evolved by subsets (as a tree):
(subsets (list 1 2 3))
|
append
____________/ \____________
/ \
(subsets '(2 3)) map consing 1
| |
append (subsets '(2 3))
____________/ \____________ |
/ \ ...
(subsets '(3)) map consing 2
____________/ \____________ |
/ \ (subsets '(3))
(subsets '()) map consing 3 |
| | ...
'(nil) (subsets '())
|
'(nil)
We can see that for each list with one element a, subsets will
return, correctly, a list l1 whose members are the empty list and
a:
(a) => ( () (a) )
What if we add one element b to the list with a? The right answer must be the list whose memembers are the members in l1 plus each member of l1 with b in it:
(a b) => ( () (a) (b) (a b))
This is exactly what subsets does: it returns the list (created by
appending) all members of l1 and each each member of l1 with b in
it (that is, the result of applying append to l1 and the map of
l1 in which we cons b in each element of l1).
What if we add one element c to the list with a and b? Analogously…
- Data abstraction permits us to:
- design programs without dealing with details of data representation,
- experiment with alternative representations.
- Here another powerful design principle fro working with data strcutures is introduced: conventional interfaces.
Consider the following two procedures. The first one computes the sum
of the squares of the odd leaves of a tree. The second one constructs
a list of all the even Fibonacci numbers up to n.
(define (sum-odd-squares tree)
(cond ((null? tree) 0)
((not (pair? tree))
(if (odd? tree) (square tree) 0))
(else (+ (sum-odd-squares
(car tree))
(sum-odd-squares
(cdr tree))))))(define (even-fibs n)
(define (next k)
(if (> k n)
nil
(let ((f (fib k)))
(if (even? f)
(cons f (next (+ k 1)))
(next (+ k 1))))))
(next 0))Those two functions don’t look very similar. However, at a certain level of abstraction, they are:
The first procedure:
- enumerates the leaves of a tree;
- filters them, selecting the odd ones;
- squares each of the selected ones; and
- accumulates the result using +, starting with 0.
The second procedure:
- enumerates the integers from 0 to n;
- computes the Fibonacci number for each integer;
- filters them, selecting the even ones; and
- accumulates the result using
cons, starting with the empty list.
These processes can be described in terms of “signals flowing through a cascade of stages”.
+-------------+ +-------------+ +-------------+ +-------------+ | enumerate: |-->| filter: |-->| map: |-->| accumulate: | | tree leaves | | odd? | | square | | +, 0 | +-------------+ +-------------+ +-------------+ +-------------+ +-------------+ +-------------+ +-------------+ +-------------+ | enumerate: |-->| map: |-->| filter: |-->| accumulate: | | integers | | fib | | even? | | cons, () | +-------------+ +-------------+ +-------------+ +-------------+
However, our two procedures fail to exhbit the signal-flow structure just described. If they did show such a structure, then we would achieve greater conceptual clarity.
{…}
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op initial (cdr sequence)))))Exercise:
Fill in the missing expressions to complete the following definitions of some basic list-manipulation operations as accumulations:
Answer:
To warmup, here is how you can use accumulate to return the list itself:
(define (list-identity sequence)
(accumulate (lambda (x y) (cons x y)) nil sequence))Given list-identity, it’s easy to write map:
(define (map p sequence)
(accumulate (lambda (x y) (cons (p x) y)) nil sequence))Append:
(define (append seq1 seq2)
(accumulate cons seq2 seq1))Length:
(define (length sequence)
(accumulate (lambda (x y) (+ 1 y)) 0 sequence))I don’t know what it means to evaluate a polynomial in x at a given value of x…
(define (count-leaves t)
(accumulate <??>
<??>
(map <??> <??>)))Hacky (cheating?) solution: just rename the old count-leaves as
count-leaves1 and:
(define (count-leaves t)
(accumulate +
0
(map count-leaves1
t)))The following solution uses map to fringe each member of t which
is a pair, producing a list of atoms and one-level-lists; then it uses
the accumulate to sum each member treated as a 1 if it’s an atom or as
the length of itself if it’s a list.
(define (map proc items)
(if (null? items)
nil
(cons (proc (car items))
(map proc (cdr items)))))
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op
initial
(cdr sequence)))))
(define (append list1 list2)
(if (null? list1)
list2
(cons (car list1)
(append (cdr list1)
list2))))
(define (fringe x)
(cond ((null? x) nil)
((not (pair? x)) (list x))
(else (append (fringe (car x))
(fringe (cdr x))))))
(define (length l)
(if (null? l)
0
(+ 1 (length (cdr l)))))
(define (gp-length l)
(if (not (pair? l))
1
(length l)))
(define (gp-count-leaves t)
(accumulate (lambda (a b)
(+ (gp-length a)
b))
0
(map fringe t)))
(gp-count-leaves '(1 (2) (((3 4 5)) 4)))This above was my solution. I’ve been told another, better, solution:
(define (dean-count-leaves t)
(accumulate +
0
(map
(lambda (x) (if (pair? x)
(dean-count-leaves x)
1)) t)))(define (accumulate-n op init seqs)
(if (null? (car seqs))
nil
(cons (accumulate op init (map car seqs))
(accumulate-n op init (map cdr seqs)))))(define (fold-right op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(fold-right op initial (cdr sequence)))))
(fold-right / 1 (list 1 2 3))
;; (/ 1 (/ 2 (/ 3 1)))
(fold-right list nil (list 1 2 3))
;; (list 1 (list 2 (list 3 nil)))
(define (fold-left op initial sequence)
(define (iter result rest)
(if (null? rest)
result
(iter (op result (car rest))
(cdr rest))))
(iter initial sequence))
(fold-left / 1 (list 1 2 3))
(/ (/ (/ 1 1) 2) 3)
(fold-left list nil (list 1 2 3))
;; (list (list (list nil 1) 2) 3)(define (reverse seq)
(fold-right (lambda (x y) (append y (list x)))
nil
seq))
(define (reverse seq)
(fold-left (lambda (x y) (append (list y) x))
nil
seq))(define (unique-pairs n)
(flatmap
(lambda (i)
(map (lambda (j)
(list i j))
(enumerate-interval
1
(- i 1))))
(enumerate-interval 1 n)))
(define (prime-sum-pairs n)
(map make-pair-sum
(filter
prime-sum?
(unique-pairs n))))Excercise:
Write a procedure to find all ordered triples of distinct positive integers i, j, and k less than or equal to a given integer n that sum to a given integer s.
Answer:
- We can:
- enumerate all ordered triples (see below how);
- filter them;
- In order to enumerate all triples:
- for each element e, enumerate all the possible pairs from 1 to n without using e, and then adjoin e to the front of each pair.
- In order to enumerate all possible pairs from 1 to n:
- for each element e of the range from 1 to n, enumerate all
other elements of the range, and for each of those other elements
create the list
(e other-element).
- for each element e of the range from 1 to n, enumerate all
other elements of the range, and for each of those other elements
create the list
(define (accumulate op initial seq)
(if (null? seq)
initial
(op (car seq)
(accumulate op initial (cdr seq)))))
(define (filter predicate seq)
(cond ((null? seq) nil)
((predicate (car seq))
(cons (car seq) (filter predicate (cdr seq))))
(else (filter predicate (cdr seq)))))
(define (enumerate-interval low high)
(if (> low high)
nil
(cons low
(enumerate-interval
(+ low 1)
high))))
(define (enumerate-interval-except low high not-allowed)
(filter (lambda (x) (not (= x not-allowed)))
(enumerate-interval low high)))
;; create a list of all possible pairs given a sequence
(define (all-pairs seq)
(accumulate
append
nil
(map (lambda (x)
(map (lambda (y)
(cons x (list y)))
(filter (lambda (e) (not (= e x))) seq)))
seq)))
;; all triples from 1 to n
(define (all-triples n)
(accumulate
append
nil
(map (lambda (x)
(map (lambda (y) (cons x y))
(all-pairs (enumerate-interval-except 1 n x))))
(enumerate-interval 1 n))))
(define (all-triples-sum n sum)
(filter (lambda (x)
(= (+ (car x)
(car (cdr x))
(car (cdr (cdr x))))
sum))
(all-triples n)))
(all-triples-sum 56 8)
;; => ((1 2 5) (1 3 4) (1 4 3) (1 5 2) (2 1 5) (2 5 1) (3 1 4) (3 4 1) (4 1 3) (4 3 1) (5 1 2) (5 2 1))(define (queens board-size)
(define (queen-cols k)
(if (= k 0)
(list empty-board)
(filter
(lambda (positions)
(safe? k positions))
(flatmap
(lambda (rest-of-queens)
(map (lambda (new-row)
(adjoin-position
new-row
k
rest-of-queens))
(enumerate-interval
1
board-size)))
(queen-cols (- k 1))))))
(queen-cols board-size))(define (filter pred seq)
(cond ((null? seq) nil)
((pred (car seq)) (cons (car seq) (filter pred (cdr seq))))
(else (filter pred (cdr seq)))))
(define (accumulate op initial seq)
(if (null? seq)
initial
(op (car seq)
(accumulate op initial (cdr seq)))))
(define (flatmap op seq)
(accumulate append nil (map op seq)))
(define (enumerate-interval low high)
(if (> low high)
nil
(cons low (enumerate-interval (+ low 1) high))))
(define (safe? k poss)
(let ((queen (car (filter
(lambda (q)
(= (car (cdr q)) k))
poss))))
(if (> (length
(filter
(lambda (p)
(or (= (car queen)
(car p))
(= (- (car p) (car queen))
(- (car (cdr p)) (car (cdr queen))))
(= (- (car p) (car queen))
(- (car (cdr queen)) (car (cdr p))))))
poss))
1)
#f
#t)))
(define (adjoin-position nr k rq)
(cons (list nr k) rq))
(define empty-board nil)
(define (queens board-size)
(define (queen-cols k)
(if (= k 0)
(list empty-board)
(filter
(lambda (positions) (safe? k positions))
(flatmap
(lambda (rest-of-queens)
(map (lambda (new-row)
(adjoin-position new-row k rest-of-queens))
(enumerate-interval 1 board-size)))
(queen-cols (- k 1))))))
(queen-cols board-size))- “…a simple language for drawing pictures that illustrates the power of data abstraction and closure, and also exploits higher-order procedures in an essential way.”
- “In this language, the data objects being combined are represented as procedures rather than as list structure.”
- the operations in this language satisfy the closure property. We are therefore capable to “build arbitrarily complicated patterns”.
- “When we began our study of programming in 1.1, we emphasized the importance of describing a language by focusing on the language’s primitives, its means of combination, and its means of abstraction. We’ll follow that framework here.”
- In this picture language there is only one kind of element: the
painter. A painter draws an image that is shifted and scaled to
fit withtin a designated parallelogram-shpaed frame.
- Painter
wave. - Painter
rogers.
- Painter
- Operations that construct painters from painters.
beside.below.flip-vertflip-horiz
- Defining
wave4. - “In building up a complex image in this manner we are exploiting the fact that painters are closed under the language’s means of combination.”
- Defining
wave4in terms offlipped-pairs. - Defining recursive operations
right-split.corner-split.
- Defining
square-limit. - Abstracting patterns of combining painter operations.
square-of-four.- Defining
flipper-pairsin terms ofsquare-of-four. - Defining
square-limitin terms ofsquare-of-four.
- A frame can be described by three vectors.
frame-coord-map.- “A painter is represented as a procedure that, given a frame as
argument, draws a particular image shifted and scaled to fit the
frame. That is to say, if
pis a painter andfis a frame, then we producep’s image infby calling p withfas argument.”(define (segments->painter segment-list) (lambda (frame) (for-each (lambda (segment) (draw-line ((frame-coord-map frame) (start-segment segment)) ((frame-coord-map frame) (end-segment segment)))) segment-list)))
Exercise:
Define the procedure
up-splitused bycorner-split. It is similar toright-split, except that it switches the roles of below and beside.
Answer:
(define (up-split painter n)
(if (= n 0)
painter
(let ((smaller (right-split painter (- n 1))))
(below painter (beside smaller smaller)))))Exercise:
Right-splitandup-splitcan be expressed as instances of a general splitting operation. Define a proceduresplitwith the property that evaluating(define right-split (split beside below)) (define up-split (split below beside))produces procedures
right-splitandup-splitwith the same behaviors as the ones already defined.
Answer:
(define (split p1 p2)
(lambda (painter n)
(if (= n 0)
painter
(let ((smaller ((split p1 p2) painter
(- n 1))))
(p1 painter
(p2 smaller smaller))))))Answer:
(define (make-vect xcor ycor)
(cons xcor ycor))
;; alternatively:
;; (define make-vect cons)
(define (xcor-vect vect)
(car vect))
;; alternatively:
;; (define xcor-vect car)
(define (ycor-vect vect)
(cdr vect))
;; alternatively
;; (define ycor-vect cdr)
(define (add-vect v1 v2)
(make-vect (+ (xcor-vect v1) (xcor-vect v2))
(+ (ycor-vect v1) (ycor-vect v1))))
(define (sub-vect v1 v2)
(make-vect (- (xcor-vect v1) (xcor-vect v2))
(- (ycor-vect v1) (ycor-vect v2))))
(define (scale-vect vect s)
(make-vect (* (xcor-vect vect) s)
(* (ycor-vect vect) s)))Answer:
(define (make-frame origin edge1 edge2)
(list origin edge1 edge2))
(define (origin-frame frame)
(car frame))
(define (edge1-frame frame)
(car (cdr frame)))
(define (edge2-frame frame)
(car (cdr (cdr frame))))(define (make-frame origin edge1 edge2)
(cons origin (cons edge1 edge2)))
(define (origin-frame frame)
(car frame))
(define (edge1-frame frame)
(car (cdr frame)))
(define (edge2-frame frame)
(cdr (cdr frame)))Exercise:
A directed line segment in the plane can be represented as a pair of vectors—the vector running from the origin to the start-point of the segment, and the vector running from the origin to the end-point of the segment. Use your vector representation from Exercise 2.46 to define a representation for segments with a constructor
make-segmentand selectorsstart-segmentandend-segment.
Answer:
(define (make-segment vector1 vector2)
(cons vector1 vector2))
(define (start-segment segment)
(car segment))
(define (end-segment segment)
(cdr segment));; Painter that draws the outline of the frame
(segments->painter
(list
(make-segment (make-vect 0 0)
(make-vect 0 1))
(make-segment (make-vect 0 1)
(make-vect 1 1))
(make-segment (make-vect 1 1)
(make-vect 1 0))
(make-segment (make-vect 1 0)
(make-vect 0 0))));; Painter that draws an ``X''
(segments->painter
(list
(make-segment (make-vect 0 0)
(make-vect 1 1))
(make-segment (make-vect 1 0)
(make-vect 0 1))));; Painter that draws a diamond
(segments->painter
(list
(make-segment (make-vect 0.5 0)
(make-vect 0 0.5))
(make-segment (make-vect 0 0.5)
(make-vect 0.5 1))
(make-segment (make-vect 0.5 1)
(make-vect 1 0.5))
(make-segment (make-vect 1 0.5)
(make-vect 0.5 0))))(define (flip-horiz painter)
(transform-painter
painter
(make-vect 1.0 0.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0)))(define (rotate-cc-180 painter)
(transform-painter
painter
(make-vect 1.0 1.0)
(make-vect 0.0 1.0)
(make-vect 1.0 0.0)))(define (rotate-cc-270 painter)
(transform-painter
painter
(make-vect 0.0 1.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0)))(define (below2 p1 p2)
(let ((paint-below (transform-painter
p1
(make-vect 0.0 0.0)
(make-vect 1.0 0.0)
(make-vect 0.0 0.5)))
(paint-above (transform-painter
p2
(make-vect 0.0 0.5)
(make-vect 1.0 0.5)
(make-vect 0.0 1.0))))
(lambda (frame)
(paint-below frame)
(paint-above frame))))
(paint (below2 einstein einstein))(define (rotate-counterclock-90 painter)
(transform-painter
painter
(make-vect 1.0 0.0)
(make-vect 1.0 1.0)
(make-vect 0.0 0.0)))
(define (rotate-clock-90 painter)
(transform-painter
painter
(make-vect 0.0 1.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0)))
(define (below3 p1 p2)
(rotate-clock-90 (beside (rotate-counterclock-90 p1)
(rotate-counterclock-90 p2))))
(paint (below3 einstein einstein))#lang sicp
(#%require sicp-pict)
(define (up-split painter n)
(if (= n 0)
painter
(let ((smaller (right-split painter (- n 1))))
(below painter (beside smaller smaller)))))
(define (right-split painter n)
(if (= n 0)
painter
(let ((smaller (right-split painter
(- n 1))))
(beside painter
(below smaller smaller)))))
;; change at the level of wave: use einstein instead
;; change at the level of corner split: swap right-split and up-split
(define (corner-split painter n)
(if (= n 0)
painter
(let ((up (right-split painter (- n 1)))
(right (up-split painter
(- n 1))))
(let ((top-left (beside up up))
(bottom-right (below right
right))
(corner (corner-split painter
(- n 1))))
(beside (below painter top-left)
(below bottom-right
corner))))))
;; change at the level of square-limit: replace fli-vert with flip-horiz
(define (square-limit painter n)
(let ((quarter (corner-split painter n)))
(let ((half (beside (flip-horiz quarter)
quarter)))
(below (flip-horiz half) half))))
(paint (square-limit einstein 3))All the compound data objects we have used so far were constructed ultimately from numbers. In this section we extend the representational capability of our language by introducing the ability to work with arbitrary symbols as data.
In order to manipulate symbols we need a new element in our language: the ability to quote a data object
(list a b) constructs a list of the values of a and b, not the
list of a and b themselves (the symbols).
As analytic philosophy students know,
[t]his issue is well known in the context of natural languages, where words and sentences may be regarded either as semantic entities or as character strings (syntactic entities)…
(In fact, footnote 98 uses an example from Frege.)
We can follow this same practice to identify lists and symbols that are to be treated as data objects rather than as expressions to be evaluated.
eq.
(define (memq item x)
(cond ((null? x) false)
((eq? item (car x)) x)
(else (memq item (cdr x)))))Exercise:
What would the interpreter print in response to evaluating each of the following expressions?
(list 'a 'b 'c) (list (list 'george)) (cdr '((x1 x2) (y1 y2))) (cadr '((x1 x2) (y1 y2))) (pair? (car '(a short list))) (memq 'red '((red shoes) (blue socks))) (memq 'red '(red shoes blue socks))
Answer:
(list 'a 'b 'c)
;; => (a b c)
(list (list 'george))
;; => ((george))
(cdr '((x1 x2) (y1 y2)))
;; => ((y1 y2))
(cadr '((x1 x2) (y1 y2)))
;; => (y1 y2)
(pair? (car '(a short list)))
;; => #f
(memq 'red '((red shoes) (blue socks)))
;; => #f
(memq 'red '(red shoes blue socks))
;; => (red shoes blue socks)(define (equal? a b)
(cond ((and (not (pair? a)) (not (pair? b)) (eq? a b))
true)
((and (and (pair? a) (pair? b))
(equal? (car a) (car b))
(equal? (cdr a) (cdr b)))
true)
(else false)))Exercise:
Eva Lu Ator types to the interpreter the expression
(car ''abracadabra)To her surprise, the interpreter prints back quote. Explain.
Answer:
From the interpreter’s perspective, 'abracadabra is actually (quote
abracadabra) (see footnote 100). And ''abracadabra is actually
(quote (quote abracadabra)). The car of the latter is indeed
quote.
(define (union-set s1 s2)
(cond ((null? s1) s2)
((null? s2) s1)
((element-of-set? (car s1) s2)
(union-set (cdr s1) s2))
(else (cons (car s1)
(union-set (cdr s1) s2)))))I wouldn’t change neither element-of-set? nor intersection-set. So
their complexity remains the same; respectively, linear and
exponential.
This is the way I would write adjoin-set:
(define (adjoin-set x set)
(cons x set))Its complexity is constant. We just have to do one operation, regardless of the size of the set.
This is the way I would write union-set:
(define (union-set s1 s2)
(if ((null? s1) s2)
(else (cons (car s1)
(union-set (cdr s1) s2)))))Its complexity is linear. We have to go through each element of one of the two lists.
(define (adjoin-set x set)
(cond ((null? set) (cons x set))
((= x (car set)) set)
((< x (car set)) (cons x set))
(else (cons (car set)
(adjoin-set x (cdr set))))))(define (union-set s1 s2)
(cond ((null? s1) s2)
((null? s2) s1)
((= (car s1) (car s2)) (cons (car s1)
(union-set (cdr s1)
(cdr s2))))
((< (car s1) (car s2)) (cons (car s1)
(union-set (cdr s1)
s2)))
((< (car s2) (car s1)) (cons (car s2)
(union-set s1
(cdr s2))))))(define (entry tree) (car tree))
(define (left-branch tree) (cadr tree))
(define (right-branch tree) (caddr tree))
(define (make-tree entry left right)
(list entry left right))
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (entry set)) true)
((< x (entry set))
(element-of-set?
x
(left-branch set)))
((> x (entry set))
(element-of-set?
x
(right-branch set)))))
(define (adjoin-set x set)
(cond ((null? set) (make-tree x '() '()))
((= x (entry set)) set)
((< x (entry set))
(make-tree
(entry set)
(adjoin-set x (left-branch set))
(right-branch set)))
((> x (entry set))
(make-tree
(entry set)
(left-branch set)
(adjoin-set x (right-branch set))))))
(define (tree->list-1 tree)
(if (null? tree)
'()
(append
(tree->list-1
(left-branch tree))
(cons (entry tree)
(tree->list-1
(right-branch tree))))))
(define (tree->list-2 tree)
(define (copy-to-list tree result-list)
(if (null? tree)
result-list
(copy-to-list
(left-branch tree)
(cons (entry tree)
(copy-to-list
(right-branch tree)
result-list)))))
(copy-to-list tree '()))
(tree->list-1 (make-tree 7
(make-tree 3
(make-tree 1 nil nil)
(make-tree 5 nil nil))
(make-tree 9
nil
(make-tree 11 nil nil))))
;; => (1 3 5 7 9 11)
(tree->list-2 (make-tree 7
(make-tree 3
(make-tree 1 nil nil)
(make-tree 5 nil nil))
(make-tree 9
nil
(make-tree 11 nil nil))))
;; => (1 3 5 7 9 11)
(tree->list-1 (make-tree 3
(make-tree 1 nil nil)
(make-tree 7
(make-tree 5 nil nil)
(make-tree 9
nil
(make-tree 11 nil nil)))))
;; => (1 3 5 7 9 11)
(tree->list-2 (make-tree 3
(make-tree 1 nil nil)
(make-tree 7
(make-tree 5 nil nil)
(make-tree 9
nil
(make-tree 11 nil nil)))))
;; => (1 3 5 7 9 11)
(tree->list-1 (make-tree 5
(make-tree 3
(make-tree 1 nil nil)
nil)
(make-tree 9
(make-tree 7 nil nil)
(make-tree 11 nil nil))))
;; => (1 3 5 7 9 11)
(tree->list-2 (make-tree 5
(make-tree 3
(make-tree 1 nil nil)
nil)
(make-tree 9
(make-tree 7 nil nil)
(make-tree 11 nil nil))))
;; => (1 3 5 7 9 11)
It looks like tree->list-1 and tree->list-2 give always the same result.
In time, they seem to grow at the same pace (Are you sure? Doesn’t the append in tree->list-1 makes it grow faster?).
In space, tree->list-2 seems to grow more slowly, because one the two recursive calls is a tail call (scheme optmizes in that case).
I’ve done a quite horrible job but here it is:
The function applies a recursive strategy. The central element of the
list given will be the entry of the tree. The central element is the
element whose index is the quotient of (- n 1) and 2, where n is
the length of the list. Then the left and the right branch are
computed. The left branch is the car of left-result, that is, the
result of the recursive call (partial-tree) applied to the original
list and the quotient of (- n 1) and 2. The result of this latter
recursive call is needed in order for computing the right branch as
well. For the right tree is the car of right-result, that is, the
recursive call (partial-tree) applied to the cdr of left-result
and
The tree produced by (list->tree '(1 3 5 7 9 11)) is:
5
/ \
/ \
/ \
/ \
1 9
\ / \
\ / \
3 7 11
- The order of growth is linear.
Exercise:
Use the results of Exercise 2.63 and Exercise 2.64 to give Θ(n) implementations of union-set and intersection-set for sets implemented as (balanced) binary trees.
Answer:
We already have a union-set (from ex 2.62) and an intersection-set
(presented by the authors) which work with ordered lists and have a
linear — O(n) — order of growth.
So, assuming that the value of the application of tree->list-1 (or
tree->list-2) is an ordered list, we can compute the union for sets
implemented as binary trees (let’s calle it union-set-bt) as
follows::
(define (union-set-bt set1 set2)
(list->tree (union-set (tree->list-1 set1)
(tree->list-1 set2)))(define (intersection-set-bt set1 set2)
(list->tree (intersection-set (tree->list-1 set1)
(tree->list-1 set2)))The order of growth of the processes evolved by union-set-bt and
intersection-set-bt procedures is linear because list->tree,
union-set and tree->list-1 (we could have alternatively used
tree-list-2) all evolve processes with linear order of growth.
Now, if we have to drop the assumption that the application of
tree->lits1/2 is going to be ordered, we can order the lists using a
sorting procedure with an order of growth of O(n) or less, for example
an implementation of merge sort. Given so, union-set-bt and
intersection-set-bt would look as follow and would still be linear:
(define (union-set-bt set1 set2)
(list->tree (union-set (sort (tree->list-1 set1))
(sort (tree->list-1 set2))))(define (intersection-set-bt set1 set2)
(list->tree (intersection-set (sort (tree->list-1 set1))
(sort ((tree->list-1 set2))))(define (key el)
(car el))
;; In this set represented as a tree, the keys are the cars of the elements.
(list->tree '( (1 "el with key 1") (2 "el with key 2") (3 "etc") (4 "foo") (6 "bar") (7 "baz")))
;; =>((3 "etc") ((1 "el with key 1") () ((2 "el with key 2") () ())) ((6 "bar") ((4 "foo") () ()) ((7 "baz") () ())))
(define (lookup given-key set)
(cond ((null? set) false)
((= given-key (key (entry set)))
(entry set))
((< given-key (key (entry set)))
(lookup given-key (left-branch set)))
(else (lookup given-key (right-branch set)))))
(lookup 3 (list->tree '( (1 "el with key 1") (2 "el with key 2") (3 "etc") (4 "foo") (6 "bar") (7 "baz"))))
;; => (3 "etc")
(lookup 8 (list->tree '( (1 "el with key 1") (2 "el with key 2") (3 "etc") (4 "foo") (6 "bar") (7 "baz"))))
;; => #fIn general, if we want to distinguish
| A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
The message `BACADAEAFABBAAAGAH’ would then be encoded as the string of 54 bits `001000010000011000100000101000001001000000000110000111’.
This A-through-H code, like the ASCII code, is a fixed-length code. There are also variable-length codes, like the Morse code.
By assigning shorter codes to frequent symbols, variable-length codes can allow for considerable savings.
With the following variable-length code
| A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|
| 0 | 100 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
We would encode the same message above in 42 bits.
However, we need a way to know when the end of a symbol is reached. One technique, used by in the Morse code, is using separators. Another solution consists in designing the code “in such a way that no complete code for any symbol is the beginning (or prefix) of the code for another symbol. Such a code is called a prefix code”.
One particular “scheme” for attaining savings by taking advantage of relative frequencies is called the Huffman encoding method.
A Huffman code can be represented as a binary tree. The leaves hold the encoded symbols pluse a weight (whose usage we shall see). Each non-leaf node holds the set of all the symbols below it and the sum of their weights.
*Figure 2.18:* A Huffman encoding tree.
(From SICP Unofficial Texinfo Format version 2.neilvandyke4 (January 10, 2007))
{A B C D E F G H} 17
*
/ \
/ \
A 8 * {B C D E F G H} 9
__________/ \_____________
/ \
{B C D} 5 * * {E F G H} 4
/ \ ___/ \___
/ \ / \
B 3 * {C D} 2 {E F} 2 * * {G H} 2
/ \ / \ / \
/ \ / \ / \
C 1 D 1 E 1 F 1 G 1 H 1
To encode: start at the root, and move down until your reach a leaf. If you go left add a 0, otherwise add a 1.
To decode: start at the root and use the 0s and 1s to decide whether to go left or right.
Initial leaves {(A 8) (B 3) (C 1) (D 1) (E 1) (F 1) (G 1) (H 1)}
Merge {(A 8) (B 3) ({C D} 2) (E 1) (F 1) (G 1) (H 1)}
Merge {(A 8) (B 3) ({C D} 2) ({E F} 2) (G 1) (H 1)}
Merge {(A 8) (B 3) ({C D} 2) ({E F} 2) ({G H} 2)}
Merge {(A 8) (B 3) ({C D} 2) ({E F G H} 4)}
Merge {(A 8) ({B C D} 5) ({E F G H} 4)}
Merge {(A 8) ({B C D E F G H} 9)}
Final merge {({A B C D E F G H} 17)}
;; Leaf constructor
(define (make-leaf symbol weight)
(list 'leaf symbol weight))
(define (leaf? object)
(eq? (car object) 'leaf))
;; Leaf selectors:
(define (symbol-leaf x) (cadr x))
(define (weight-leaf x) (caddr x))
;; Tree constructor:
(define (make-code-tree left right)
(list left
right
(append (symbols left) (symbols right))
(+ (weight left) (weight right))))
;; Tree selectors:
(define (left-branch tree) (car tree))
(define (right-branch tree) (cadr tree))
(define (symbols tree)
(if (leaf? tree)
(list (symbol-leaf tree))
(caddr tree)))
(define (weight tree)
(if (leaf? tree)
(weight-leaf tree)
(cadddr tree)))(define (decode bits tree)
(define (decode-1 bits current-branch)
(if (null? bits)
'()
(let ((next-branch
(choose-branch (car bits) current-branch)))
(if (leaf? next-branch)
(cons (symbol-leaf next-branch)
(decode-1 (cdr bits) tree))
(decode-1 (cdr bits) next-branch)))))
(decode-1 bits tree))
(define (choose-branch bit branch)
(cond ((= bit 0) (left-branch branch))
((= bit 1) (right-branch branch))
(else (error "bad bit -- CHOOSE-BRANCH" bit))))(define (adjoin-set x set)
(cond ((null? set) (list x))
((< (weight x) (weight (car set))) (cons x set))
(else (cons (car set)
(adjoin-set x (cdr set))))))
(define (make-leaf-set pairs)
(if (null? pairs)
'()
(let ((pair (car pairs)))
(adjoin-set (make-leaf (car pair) ; symbol
(cadr pair)) ; frequency
(make-leaf-set (cdr pairs))))))Exercise:
Define an encoding tree and a sample message:
(define sample-tree (make-code-tree (make-leaf 'A 4) (make-code-tree (make-leaf 'B 2) (make-code-tree (make-leaf 'D 1) (make-leaf 'C 1))))) (define sample-message '(0 1 1 0 0 1 0 1 0 1 1 1 0))Use the
decodeprocedure to decode the message, and give the result.
Answer:
(define (make-leaf symbol weight)
(list 'leaf symbol weight))
(define (leaf? object)
(eq? (car object) 'leaf))
(define (symbol-leaf x) (cadr x))
(define (weight-leaf x) (caddr x))
(define (make-code-tree left right)
(list left
right
(append (symbols left)
(symbols right))
(+ (weight left) (weight right))))
(define (left-branch tree) (car tree))
(define (right-branch tree) (cadr tree))
(define (symbols tree)
(if (leaf? tree)
(list (symbol-leaf tree))
(caddr tree)))
(define (weight tree)
(if (leaf? tree)
(weight-leaf tree)
(cadddr tree)))
(define (decode bits tree)
(define (decode-1 bits current-branch)
(if (null? bits)
'()
(let ((next-branch
(choose-branch
(car bits)
current-branch)))
(if (leaf? next-branch)
(cons
(symbol-leaf next-branch)
(decode-1 (cdr bits) tree))
(decode-1 (cdr bits)
next-branch)))))
(decode-1 bits tree))
(define (choose-branch bit branch)
(cond ((= bit 0) (left-branch branch))
((= bit 1) (right-branch branch))
(else (error "bad bit:
CHOOSE-BRANCH" bit))))
(define (adjoin-set x set)
(cond ((null? set) (list x))
((< (weight x) (weight (car set)))
(cons x set))
(else
(cons (car set)
(adjoin-set x (cdr set))))))
(define (make-leaf-set pairs)
(if (null? pairs)
'()
(let ((pair (car pairs)))
(adjoin-set
(make-leaf (car pair) ; symbol
(cadr pair)) ; frequency
(make-leaf-set (cdr pairs))))))
(define sample-tree
(make-code-tree
(make-leaf 'A 4)
(make-code-tree
(make-leaf 'B 2)
(make-code-tree
(make-leaf 'D 1)
(make-leaf 'C 1)))))
(define sample-message
'(0 1 1 0 0 1 0 1 0 1 1 1 0))
(decode sample-message sample-tree) ;; (A D A B B C A)Exercise:
The
encodeprocedure takes as arguments a message and a tree and produces the list of bits that gives the encoded message.(define (encode message tree) (if (null? message) '() (append (encode-symbol (car message) tree) (encode (cdr message) tree))))
Encode-symbolis a procedure, which you must write, that returns the list of bits that encodes a given symbol according to a given tree. You should designencode-symbolso that it signals an error if the symbol is not in the tree at all. Test your procedure by encoding the result you obtained in Exercise 2.67 with the sample tree and seeing whether it is the same as the original sample message.
Answer:
(define (element-of-set? x set)
(cond ((null? set) false)
((equal? x (car set)) true)
(else (element-of-set? x (cdr set)))))
(define (encode-symbol sym tree)
(cond ((element-of-set? sym (symbols tree))
(if (element-of-set? sym (symbols (left-branch tree)))
(if (leaf? (left-branch tree))
'(0)
(cons 0 (encode-symbol sym (left-branch tree))))
(if (leaf? (right-branch tree))
'(1)
(cons 1 (encode-symbol sym (right-branch tree))))))
(else (error "Cannot encode symbol :( Symbol is not in the tree"))))- comments:
- the check for error could be done just once.
- simplify the conditions?
- are the symbols ordered? I don’t remember. In that case we could
use a more performant
element-of-set?. (Anyway,element-of-set?is an abstraction…).
Exercise:
The following procedure takes as its argument a list of symbol-frequency pairs (where no symbol appears in more than one pair) and generates a Huffman encoding tree according to the Huffman algorithm.
(define (generate-huffman-tree pairs) (successive-merge (make-leaf-set pairs)))`Make-leaf-set’ is the procedure given above that transforms the list of pairs into an ordered set of leaves. `Successive-merge’ is the procedure you must write, using `make-code-tree’ to successively merge the smallest-weight elements of the set until there is only one element left, which is the desired Huffman tree. (This procedure is slightly tricky, but not really complicated. If you find yourself designing a complex procedure, then you are almost certainly doing something wrong. You can take significant advantage of the fact that we are using an ordered set representation.)
Answer:
(define (successive-merge pairs)
(cond ((null? pairs) nil)
((null? (cdr pairs)) (car pairs))
(else (successive-merge
(adjoin-set (make-code-tree (car pairs) (cadr pairs))
(cddr pairs))))))The following eight-symbol alphabet with associated relative frequencies was designed to efficiently encode the lyrics of 1950s rock songs. (Note that the “symbols” of an “alphabet” need not be individual letters.)
A 2 NA 16 BOOM 1 SHA 3 GET 2 YIP 9 JOB 2 WAH 1Use
generate-huffman-tree(Exercise 2.69) to generate a corresponding Huffman tree, and useencode(Exercise 2.68) to encode the following message:Get a job Sha na na na na na na na na Get a job Sha na na na na na na na na Wah yip yip yip yip yip yip yip yip yip Sha boomHow many bits are required for the encoding? What is the smallest number of bits that would be needed to encode this song if we used a fixed-length code for the eight-symbol alphabet?
(define rock-tree
(generate-huffman-tree
'((A 2) (NA 16) (BOOM 1) (SHA 3) (GET 2) (YIP 9) (JOB 2) (WAH 1))))
(encode '(GET A JOB
SHA NA NA NA NA NA NA NA NA
GET A JOB
SHA NA NA NA NA NA NA NA NA
WAH YIP YIP YIP YIP
YIP YIP YIP YIP YIP
SHA BOOM)
rock-tree)84 bits are required.
If we used a fixed-length code, given that we have 8 symbols, we would need 3 bits for each symbol (Cf. p.161). The song is made of 36 symbols, so to encode it with a fixed-length code we would need (* 36 3) = 108 bits.
Exercise:
Suppose we have a Huffman tree for an alphabet of n symbols, and that the relative frequencies of the symbols are $1,2,4,…,2n−1$. Sketch the tree for
$n=5$ ; for$n=10$ . In such a tree (for general$n$ ) how many bits are required to encode the most frequent symbol? The least frequent symbol?
Answer:
;; for n = 5:
;; (((((leaf A 1) (leaf B 2) (A B) 3) (leaf C 4) (A B C) 7)
;; (leaf D 8) (A B C D) 15) (leaf E 16) (A B C D E) 31)
;;
;; *
;; _____|____
;; | |
;; * E 16
;; ____|____
;; | |
;; * D 8
;; ____|____
;; | |
;; * C 4
;; |
;; ____*____
;; | |
;;
;; A 1 B 2
;; Analogously for n = 10...
;; The newly created tree at each step of successive-merge is placed
;; at the start, because its weight is one value less than then next
;; element.We need only 1 bit to represent the most frequent symbol.
We need
Consider the encoding procedure that you designed in Exercise 2.68. What is the order of growth in the number of steps needed to encode a symbol? Be sure to include the number of steps needed to search the symbol list at each node encountered. To answer this question in general is difficult. Consider the special case where the relative frequencies of the
$n$ symbols are as described in Exercise 2.71, and give the order of growth (as a function of$n$ ) of the number of steps needed to encode the most frequent and least frequent symbols in the alphabet.
Data Abstraction keeps separate the use from the implementation, the interface from the representation.
A Scheme programmer, for example, usually operates at a level of
abstraction such that she doesn’t have to worry about how car,
cdr, and cons are implemented. She just has to know how they
behave. She just has to know that cons takes two entities and
creates a further entity — aptly called a “pair”— the
application of car to which returns the first entity and the
application of cdr to which returns the second entity. The
implementation of how this works remains in the shadows. The
programmer knows how to use pairs, but she doens’t have to know how
pairs are represented.
Section 2.1.1 showed a example of this kinds of “abstractions barriers”. We saw there “how to separate the task of designing a program that uses rational numbers from the task of implemententing rational numbers. The “abstractions barriers” we are talking about can be thought of as horizontal barriers which are present at different levels (see Figure 2.1). In that specific example, there are the following barriers:
cons,car,cdr;make-rat,numer,denom;add-rat,sub-rat, etc.;- programs that use rational numbers.
Despite the benefits that those barriers provide, those barriers are not enough. They are not enough, because there might be more than one useful representation for a certain data object and we might want to use all of them in our system. Complex numbers offer a more-or-less-toy example. Complex numbers can be represented in the so-called “rectangular” form — which is in terms of a real part and an imaginary part —, or in the so-called “polar” form — which is in terms of a magnitude and an angle. Each of those two representations is more appropriate than the other in certain circumstances.
We need:
- NOT ONLY: “data-abstraction barriers” that isolate use from representation, interface from implementation,
- BUT ALSO: abstraction barriers that isolate different representations for the same data object and allow those different design choices to coexist.
- MOREOVER: we need to able to add a certain representation to a system additively, that is, without having to redesign or reimplement it.
You can think of those additional barriers as vertical barriers (see Figure 2.19).
*Figure 2.19:* Data-abstraction barriers in the complex-number
system.
Programs that use complex numbers
+-------------------------------------------------+
--| add-complex sub-complex mul-complex div-complex |--
+-------------------------------------------------+
Complex arithmetic package
---------------------------+---------------------------
Rectangular | Polar
representation | representation
---------------------------+---------------------------
List structure and primitive machine arithmetic
[Figure from SICP Unofficial Texinfo Format version 2.neilvandyke4 (January 10, 2007)]
THE ANSWER is generic procedures:
“procedures that can operate on data that may be represented in more than one way”.
We will be able to write generic procedure thanks to the usage of type tags. To achieve the ability to add representation to a certain system additively we will use the tecnnique of data-directed programming.
- Selectors and constructors that are our abstract data:
- Selectors:
real-part;imag-part;magnitude;angle;
- Constructors:
make-from-real-imag;make-from-mag-ang;
- Selectors:
- We can specify operations on complex numbers in terms of the
abstract data above:
add-complex;sub-complex;mul-complex;div-complex;
- Suppose that Ben and Alyssa have implemented two different representations, the selectors and the constructors they have created have the same name but they operate differently underneath the hood.
- Given that the operations add-complex, sub-complex, mul-complex, and div-complex are implemented in terms of abstract data, adopting Ben’s representation or Alyssa’s would make no difference: those operations would work in both cases.
Division1 could provide its package like that:
(define (install-division1-package)
;; internal procedures
(define (get-record file employee-name)
;; ...
)
;; interface to the rest of the system
(define (tag-file x) (attach-tag 'division1 x))
(define (tag-employee x) (attach-tag 'employee-division1 x))
(put 'get-record '(division1 employee-division1) get-record))Other division would do anologously.
A generic get-record procedure could then be implemented as follows:
(define (get-record personnel-file name)
(apply-generic 'get-record personnel-file name))(define (make-from-mag-ang r a)
(define (dispatch op)
(cond ((eq? op 'real-part) (* r (cos a)))
((eq? op 'imag-part) (* r (sin a)))
((eq? op 'magnitude) r)
((eq? op 'angle) a)
(else (error "Unknown op - MAKE-FROM-MAG-ANG" op))))
dispatch)As a large system with generic operations evolves, new types of data objects or new operations may be needed. For each of the three strategies — generic operations with explicit dispatch, data-directed style, and message-passing-style — describe the changes that must be made to a system in order to add new types or new operations. Which organization would be most appropriate for a system in which new types must often be added? Which would be most appropriate for a system in which new operations must often be added?
Let’s imagine Henry wants to add his representation to the complex number arithmetic system.
Somebody (the “manager”…) has to change all generic operators.
real-part, imag-part, magnitude, angle, now need an additonal
check for Henry’s representation. Moreover, Henry should make sure
that the names of his procedures don’t conflict with those used by Ben
and Alyssa.
Suppose we need a get-foo operation.
All of those in charge of maintaining representation (Ben, Alyssa, and Henry) have to write a method that performs the right operation with their representation. And, again, name conflict is to be avoided.
Moreover, somebody (the “manager”…) has to write a generic
get-foo operation. In order to do so, he has to know all the names
of the procedures written by Ben, Alyssa, and Henry.
Again, let’s imagine that Henry wants to add his representation to the complex number arithmetic system we already have.
Herry, in data-directed system, has to “install” his packaged, that is, he has to put his procedures into the table.
By following the method shown at p. ? he doesn’t have to worry about name conflict (That method exploits scope. There are other ways as well; for example, putting lambdas into the table. The table stores objects, not names).
There is now work for the “manager”. The manager has been
“automated out of existence” (ref: ). The generic operations we
already have will do the right thing thanks to apply-generic (or its
simpler version operate shown in the lecture).
Again, suppose we need a get-foo operation.
Sombody has to write a generic get-foo.
However, unlike with generic operations with explicit dispatch, now we don’t need to know anything besides the name of the operation we want to add.
Each package mantainer will have the responsibility to add their
version of get-foo to the table. However, in case one doesn’t and we
try to get-foo to complext number of their type, the generic
operation will show a suitable error message.
Again, let’s imagine that Henry wants to add his representation to the complex number arithmetic system we already have.
Henry just as to add a new constructor. The situation is somewhat analogous to the data-directed programming case.
Again, suppose we need a get-foo operation.
Somebody has to write the generic operation get-foo, like in
data-directed programming.
Moreove, each “packgage maintainers” will have to add their version
of get-foo in the dispatch procedure. In this case as well, if
somebody forgets to add the procedures, an error message is printed
when we apply get-foo on the releavant object.
(
One weakness is that the generic interface procedures (`real-part’, `imag-part’, `magnitude’, and `angle’) must know about all the different representations. For instance, suppose we wanted to incorporate a new representation for complex numbers into our complex-number system. We would need to identify this new representation with a type, and then add a clause to each of the generic interface procedures to check for the new type and apply the appropriate selector for that representation.
Another weakness of the technique is that even though the individual representations can be designed separately, we must guarantee that no two procedures in the entire system have the same name. This is why Ben and Alyssa had to change the names of their original procedures from section *Note 2-4-1.
)
Okay, let’s see what happens with generic operations with explicit dispatch.
Let’s start from the particular and then we’ll try to generalize.
Let’s consider the complex number system in 2.4.2. Suppose that Richard comes up with a new way to represent complex numbers in terms of a foo and a bar. Richard has to write some analogous code to that of Ben and that of Alyssa in 2.4.2. That is, Richard had to provide a constructor and some selectors:
(define (foo-part-Richard z) ...)
(define (bar-part-Richard z) ...)
(define (make-from-foo-bar foo bar)
(attach-tag 'Richard
...))Richard, also, has to look at what other representations there are in the system and provide the correspondent selectors and constructors (in our case there are two other representations: Ben’s and Alyssa’s. The former is in terms of a real and an imaginary part. The latter in terms of a magnitude and an angle.):
(define (real-part-Richard z) ...)
(define (imag-part-Richard z) ...)
(define (magnitude-Richard z) ...)
(define (angle-rectangular z) ...)
(define (make-from-real-imag-Richard x y)
(attach-tag 'Richard
...))
(define (make-from-mag-ang-Richard r a)
(attach-tag 'Richard
...))Moreover, now Ben and Alyssa should support Richard’s representation:
;; Ben:
(define (foo-part-rectangular z) ...)
(define (bar-part-rectangular z) ...)
(define (make-from-foo-bar-rectangular x y)
(attach-tag 'rectangular ...))
;; Alyssa:
(define (foo-part-polar z) ...)
(define (bar-part-polar z) ...)
(define (make-from-foo-bar-polar r a)
(attach-tag 'polar ...))Then, each generic selectors should be updated. Each of them now
should include an additional check for the Richard type. For example,
real-part should now look something like this:
(define (real-part z)
(cond ((rectangular? z)
(real-part-rectangular (contents z)))
((polar? z)
(real-part-polar (contents z)))
((Richard? z)
(real-part-Richard (contents z)))
(else (error "Unknown type -- REAL-PART" z))))Finally, a generic constructor should be provided (different implementations are possible.)
(define (make-from-foo-bar
...))Our system now has now four generic complex numbers operations:
div-complex, sub-complex, add-complex, and mul-complex.
Now we want to add new-operation to the system.
What happens?
Assuming new-operation is defined in terms of the general
constructors and the generic selectors present in the system, then we
should just define it:
(define (new-operation z1 z2)
(...))Let’s assumed that Ben’s and Alyssa’s representations are now part of data-directed system as described in 2.4.3. Richard comes along and wants to add his package to the system. What does Richard have to do?
Well, he has to define a package and interface it with the rest of the system. He can do it by calling the following procedure:
(define (install-Richard-package)
;; internal procedures
(define (foo-part z) ...)
(define (bar-part z) ...)
(define (make-from-foo-bar z) ...)
(define (real-part z) ...)
(define (imag-part z) ...)
(define (make-from-real-imag x y) ...)
(define (magnitude z) ...)
(define (angle z) ...)
(define (make-from-mag-ang r a) ...)
;; interface to the rest of the system
(define (tag x) (attach-tag 'Richard x))
(put 'foo-part '(Richard) foo-part)
(put 'bar-part '(Richard) bar-part)
(put 'real-part '(Richard) real-part)
(put 'imag-part '(Richard) imag-part)
(put 'magnitude '(Richard) magnitude)
(put 'angle '(rectangular) angle)
(put 'make-from-foo-bar 'Richard
(lambda (f b) (tag (make-from-foo-bar f b))))
(put 'make-from-real-imag 'rectangular
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'rectangular
(lambda (r a) (tag (make-from-mag-ang r a))))
'done)Once Richard’s procedures have been installed into the table, we can define generic selectors:
(define (foo-part z) (apply-generic 'foo-part z))
(define (bar-part z) (apply-generic 'bar-part z))And a generic constructor:
(define (make-from-foo-bar x y)
((get 'make-from-foo-bar 'Richard) x y))Ben’s and Alyssa’s packages don’t need to know about Richard’s. They don’t have to change anything.
(It is true thought that if one applies foo-part (or bar-part) to
a complex number which hasn’t been implemented using Richard
representation, then apply-generic won’t find any method for that
type, and an error will be raised. If we want foo-part and
bar-part to work with representation other than Richard’s, the
packages of those presentations are to be modified so that they
include the relevant methods.)
Same as in “Generic operations with explicit dispatch”?
In 2.5.1, Authors show how to define generic operations that can take different types of arguments (numbers) by using the same technique which has been used to define the generic operations (selectors) in the case of complex numbers (in 2.4.3).
Exercise:
Louis Reasoner tries to evaluate the expression
(magnitude z)wherezis the object shown in *Note Figure 2-24. To his surprise, instead of the answer 5 he gets an error message from `apply-generic’, saying there is no method for the operationmagnitudeon the types(complex). He shows this interaction to Alyssa P. Hacker, who says “The problem is that the complex-number selectors were never defined forcomplexnumbers, just forpolarandrectangularnumbers. All you have to do to make this work is add the following to thecomplexpackage:”(put 'real-part '(complex) real-part) (put 'imag-part '(complex) imag-part) (put 'magnitude '(complex) magnitude) (put 'angle '(complex) angle)Describe in detail why this works. As an example, trace through all the procedures called in evaluating the expression
(magnitude z)wherezis the object shown in *Note Figure 2-24. In particular, how many times isapply-genericinvoked? What procedure is dispatched to in each case?
Answer:
Here is z:
-->[o|o]-->[o|o]-------->[o|o]
| | | |
v v v v
'complex 'rectangular 3 4
Louis evaluates (magnitude z).
Louis is using the procedure defined as follows:
(define (magnitude z)
(apply-generic 'magnitude z))This means that when calling magnitude, the first thing we do is
looking in the table for the item specified by the row 'magnitude
and column 'complex (the type of z).
However, nobody has stored such a table item. (At the moment there is
an element specified by row 'magnitude and column 'rectangular,
and an element specified by row 'magnitude and column 'polar.) So,
Louis’s invocation produces an error.
Alyssa’s code adds to the table four objects. Those objects are the generic procedures defined on page 84, which are themselves designed to look for and use an object in the table.
So, now, when Louis calls (magnitude z), we look for a table item
which exists. It’s the item which has been installed by Alyssa with
this line:
(put 'magnitude '(complex) magnitude)Given that we find an item in the table, apply-generic applies it to
the contents of z. Now, what’s the found table item? And what are
the contents of z. Let’s start from the latter. These are the
contents of z:
[o|o]------>[o|o]
| | |
v v v
'rectangular 3 4
Applying magnitude to these contents means, again, looking for an
item in the table. This time we are looking for the item specified the
row 'magnitude and the colum 'rectangular. An item is found and
applied to the contents.
Table before Alyssa’s change:
| rectangular | polar | |
|---|---|---|
| … | ||
| magnitude | magnitude-rectangular | magnitude-polar |
| … |
Table after Alyssa’s change:
| complex | rectangular | polar | |
|---|---|---|---|
| … | |||
| magnitude | magnitude | magnitude-rectangular | magnitude-polar |
| … |
When evaluating (magnitude z), after Alyssa’s contribution,
apply-generic is called twice. The first time it dispatches to
magnitude to itself (in a sense, magnitude, through
apply-generic, is dispatching to itself). The second time it
dispatches to magnitude-rectangular.
(magnitude z) ;; z: -->[o|o]-->[o|o]-------->[o|o]
;; | | | |
;; v v v v
;; 'complex 'rectangular 3 4
;; |
;; |
;; V
;; apply-generic
;; |
;; |
;; V
(magnitude z') ;; z': -->[o|o]-------->[o|o]
;; | | |
;; v v v
;; 'rectangular 3 4
;; |
;; |
;; V
;; apply-generic
;; |
;; |
;; V
(magnitude z'') ;; z'': -->[o|o]
;; | |
;; v v
;; 3 4
Basically, Alyssa’s line, has the effect of making magnitude
stripping off 'complex before dispatching to someone else.
Exercise:
The internal procedures in the
scheme-numberpackage are essentially nothing more than calls to the primitive procedures+,-, etc. It was not possible to use the primitives of the language directly because our type-tag system requires that each data object have a type attached to it. In fact, however, all Lisp implementations do have a type system, which they use internally. Primitive predicates such assymbol?andnumber?determine whether data objects have particular types. Modify the definitions oftype-tag,contents, andattach-tagfrom section *Note 2-4-2:: so that our generic system takes advantage of Scheme’s internal type system. That is to say, the system should work as before except that ordinary numbers should be represented simply as Scheme numbers rather than as pairs whosecaris the symbolscheme-number.
Answer:
(define (type-tag datum)
(cond ((number? datum) 'scheme-number)
((pair? datum) (car datum))
(else (error "Bad tagged datum -- TYPE-TAG" datum))))
(define (contents datum)
(cond ((number? datum) datum)
((pair? datum) (cdr datum))
(else (error "Bad tagged datum -- CONTENTS" datum))))
(define (attach-tag type-tag contents)
(if (number? contents)
contents
(cons type-tag contents)))
;; alternatively
(define (attach-tag type-tag contents)
(if (eq? type-tag 'scheme-number)
contents
(cons type-tag contents)))Exercise:
Define a generic equality predicate `equ?’ that tests the equality of two numbers, and install it in the generic arithmetic package. This operation should work for ordinary numbers, rational numbers, and complex numbers.
Answer:
I guess, first of all:
(define (equ x y) apply-generic 'equ x y)After this, we should put the specific procedures for the types of numbers we have:
(put 'equ '(scheme-number scheme-number)
(lambda (x y) (= x y)))(put 'equ '(rational rational)
(lambda (x y) (and (= (car x) (car y))
(= (cdr x) (cdr y)))))(if equ for rational numbers was defined within the
install-rational-package procedure we could make use of number and
denom)
(put 'equ '(complex complex)
(lambda (x y) (and (= (real-part x) (real-part y))
(= (imag-part x) (imag-part y)))))(Real-part and imag-part, if I’m not wrong, here work correctly
thanks to the code added by Alyssa P. Hacker in ex. 2.77.)
(Alternatively, we could have used magnitude and angle, instead of
real-part and imag-part.)
Exercise:
Define a generic predicate `=zero?’ that tests if its argument is zero, and install it in the generic arithmetic package. This operation should work for ordinary numbers, rational numbers, and complex numbers.
Answer:
(define (zero? x)
(apply-generic zero? x))(put 'zero '(scheme-number scheme-number)
(lambda (x) (= x 0)))(put 'zero '(rational rational)
(lambda (x)
(and (= (car x) 0)
(not (= (cdr x) 0)))))
;; the numerator must be zero and the denominator must be non-zero(put 'zero '(complex)
(lambda (x)
(and (= (real-part x) 0)
(= (imag-part x) 0))))Alternatively:
(put 'zero '(complex)
(lambda (x)
(= (angle x) 0)))So far we have considered operations on objects of the same type.
For example, the addition of two ordinary numbers or the multiplication of two rational numbers.
But this means that the operations we have defined “treat the different data types as being completely independent.”. We haven’t dealt with, say the addition of an ordinary number and a rational number, or the division of a rational number and a complex number.
How should we introduce “cross-type” operations in our system?
One way to handle cross-type operations is to design a different procedure for each possible combination of types for which the operation is valid. […] This technique works, but it is cumbersome.
When we can, we should be “by taking advantage of additional structure that may be latent in our type system”: often an object of a certain data type can be seen as an object of a another data type. E.g., the rational number 2/2, can be seen as the ordinary number 1. Given so, if we are asked to perform an operation on a rational number and an ordinary number, we could try to “coerce” the rational number into an ordinary number. And if we are successfull in doing so, then we can use our good old procedure that works with ordinary numbers.
The coercion idea can be implement by designing coercion procedures,
installing them into a coercion table, and then modifying
apply-generic.
(define (scheme-number->complex n)
(make-complex-from-real-imag (contents n) 0))
(put-coercion 'scheme-number 'complex scheme-number->complex)
;; For simplicity, only the case in which there are two arguments is
;; considered
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(if (= (length args) 2)
(let ((type1 (car type-tags))
(type2 (cadr type-tags))
(a1 (car args))
(a2 (cadr args)))
(let ((t1->t2 (get-coercion type1 type2))
(t2->t1 (get-coercion type2 type1)))
(cond (t1->t2
(apply-generic op (t1->t2 a1) a2))
(t2->t1
(apply-generic op a1 (t2->t1 a2)))
(else
(error "No method for these types"
(list op type-tags))))))
(error "No method for these types"
(list op type-tags)))))))This coercion scheme is useful, but not general enough: there may be cases in which it’s not possible neither object can be converted into the type of the other object, but in which both objects could be converted to a third type.
Exercise:
Louis Reasoner has noticed that
apply-genericmay try to coerce the arguments to each other’s type even if they already have the same type. Therefore, he reasons, we need to put procedures in the coercion table to “coerce” arguments of each type to their own type. For example, in addition to thescheme-number->complexcoercion shown above, he would do:(define (scheme-number->scheme-number n) n) (define (complex->complex z) z) (put-coercion 'scheme-number 'scheme-number scheme-number->scheme-number) (put-coercion 'complex 'complex complex->complex)a. With Louis’s coercion procedures installed, what happens if
apply-genericis called with two arguments of typescheme-numberor two arguments of typecomplexfor an operation that is not found in the table for those types? For example, assume that we’ve defined a generic exponentiation operation:(define (exp x y) (apply-generic 'exp x y))and have put a procedure for exponentiation in the Scheme-number package but not in any other package:
;; following added to Scheme-number package (put 'exp '(scheme-number scheme-number) (lambda (x y) (tag (expt x y)))) ; using primitive `expt'What happens if we call
expwith two complex numbers as arguments?b. Is Louis correct that something had to be done about coercion with arguments of the same type, or does
apply-genericwork correctly as is?c. Modify
apply-genericso that it doesn’t try coercion if the two arguments have the same type.
Answer:
If we call exp with two complex numbers, we would call
(apply-generic 'exp CN1 CN2)We are not going to find a procedure, because we don’t have an object
in the table for row 'exp and column '(complex complex).
So we would go inside the second if block.
Both t1->t2 and t2->t1 would be truthy, thanks to the code added
by Louis Reasoner.
Given that the former is truthy, we call
(apply-generic 'exp (t1->t2 CN1) CN2)(t1->t2 CN1) evaluates to CN1, so we are calling apply-generic
again with its original arguments. So: we would be calling
apply-generic ad infinitum with the same arguments.
Suppose we try to add two complex numbers:
(add CN1 CN2)
; |
; V
(apply-generic 'add '(complex complex))
;; |
;; VWe find an object in the table (the right procedure) and we do not try to coerce anything.
What about rational numbers?
(add RN1 RN2)
; |
; VSame!
So, I don’t think that Louis Reasoner is correct.
However, the c. part of this exercise tells me that I am wrong!
So, what are the contexts in which apply-generic would try to coerce
arguments of the same type?
First thought: when (obviously) the args are of the same type, and there is no relevant object in the table.
In fact, in a., we are given the example of 'exp.
What happens if we call exp with two rational numbers or complex
numbers without the additional code provided by Louis Reasoner?
(exp CN1 CN2)
; |
; V
(apply-generic 'exp '(complex complex))
; |
; Vapply-generic would not find a proc (when it uses get), and so
(given that (= (length args) 2) is true) is going to call
get-coercion twice.
So, yeah, Louis Reasoner was right.
In this case we would be calling (get-coercion 'complex 'complex).
My first instinct is to turn
(if (= (length args) 2)into
(if (and (= (length args) 2)
(eq (car (type-tags))
(cadr (type-tags))))There might be more elegant ways of doing it, but this should work. Here is the modified procedure:
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(if (and (= (length args) 2)
(eq (car (type-tags))
(cadr (type-tags))))
(let ((type1 (car type-tags))
(type2 (cadr type-tags))
(a1 (car args))
(a2 (cadr args)))
(let ((t1->t2 (get-coercion type1 type2))
(t2->t1 (get-coercion type2 type1)))
(cond (t1->t2
(apply-generic op (t1->t2 a1) a2))
(t2->t1
(apply-generic op a1 (t2->t1 a2)))
(else
(error "No method for these types"
(list op type-tags))))))
(error "No method for these types"
(list op type-tags)))))))Show how to generalize `apply-generic’ to handle coercion in the general case of multiple arguments. One strategy is to attempt to coerce all the arguments to the type of the first argument, then to the type of the second argument, and so on. Give an example of a situation where this strategy (and likewise the two-argument version given above) is not sufficiently general. (Hint: Consider the case where there are some suitable mixed-type operations present in the table that will not be tried.)
Authors are telling us what to try: “One strategy is to attempt to coerce all the arguments to the type of the first argument, then to the type of the second argument, and so on.”
So we need to “loop” over the arguments and, for each one of them, we get the type of the type and try to coerce all the others. This “double loop” operation probably lends itself to be handled in some elegant way using higher-order procedures.
In the following approach, if the first retrival of proc fails, I’m going to loop over each argument using procedural iteration. I create the list of the functions needed from the coercion table, and create, if possible (if I’ve found all relevant procedures), the list of all coerced arguments. We then try to retrieve the relevant proc again. I we succeed we can call apply, otherwise we keep iterating.
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(apply-generic-coerce 0 op . args)))))
(define (apply-generic-coerce i op . args)
(if (>= i (length args))
(error "failed to find op")
;; find type of args with index i
(let ((type (type-tag (list-ref args i))))
;; build a list of all the functions that are needed from the coercion table
;; (when the type is the same we can just use the identity function.
(let ((coercing-funs (map (lambda (arg)
(if (eq? (type-tag arg) type)
identity
(get-coercion (type-tag arg) type)))
args)))
(if (> (length (filter is-falsy coercing-funs) 0)
;; try with next type
(apply-generic-coerce (+ 1 i) op . args)
(let ((coerced-args (map (lambda (arg)
((get-coercion (type-tag arg) type) arg)))))
(let ((proc (get op (map type-tags coerced-args))))
(if proc
;; found proc!
(apply proc (map contents coerced-args))
;; try with next type
(apply-generic-coerce (+ 1 i) op . args))))))))))I suspect that the situations in which the procedure is not going to work are those situation in which we have to coerce to some arguments to some type which is not the type of other arguments.
For example if we have in the table an opration foo which works on triangles and we try to apply it to on isosceles triangle and a right triangle, trying to coerce the isosceles to right or viceversa will not work. We will have instead to coerce both the isosceles and the right tringles to tringle.
Exercise:
An accumulator is a procedure that is called repeatedly with a single numeric argument and accumulates its arguments into a sum. Each time it is called, it returns the currently accumulated sum. Write a procedure
make-accumulatorthat generates accumulators, each maintaining an independent sum. The input tomake-accumulatorshould specify the initial value of the sum; for example(define A (make-accumulator 5)) (A 10) 15 (A 10) 25
Answer:
(define (make-accumulator initial)
(lambda (val)
(begin (set! initial (+ val initial))
initial)))
(define A (make-accumulator 5))
(A 10) ;; => 15
(A 10) ;; => 25
(define B (make-accumulator 938))
(B 1) ;; => 939
(B 2) ;; => 941Exercise:
In software-testing applications, it is useful to be able to count the number of times a given procedure is called during the course of a computation. Write a procedure `make-monitored’ that takes as input a procedure,
f, that itself takes one input. The result returned bymake-monitoredis a third procedure, saymf, that keeps track of the number of times it has been called by maintaining an internal counter. If the input tomfis the special symbolhow-many-calls?, thenmfreturns the value of the counter. If the input is the special symbolreset-count, thenmfresets the counter to zero. For any other input,mfreturns the result of callingfon that input and increments the counter. For instance, we could make a monitored version of thesqrtprocedure:(define s (make-monitored sqrt)) (s 100) 10 (s 'how-many-calls?) 1
Answer:
(define (make-monitored f)
(let ((counter 0))
(lambda (x)
(cond ((eq? x 'how-many-calls?) counter)
((eq? x 'reset-count) (set! counter 0))
(else (begin (set! counter (+ counter 1))
(f x)))))))
(define s (make-monitored sqrt))
(s 100) ;; => 10
(s 'how-many-calls?) ;; => 1Exercise:
Modify the
make-accountprocedure so that it creates password-protected accounts. That is,make-accountshould take a symbol as an additional argument, as in(define acc (make-account 100 'secret-password))The resulting account object should process a request only if it is accompanied by the password with which the account was created, and should otherwise return a complaint:
((acc 'secret-password 'withdraw) 40) 60 ((acc 'some-other-password 'deposit) 50) "Incorrect password"
Answer:
(define (make-account balance pwd)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(define (dispatch p m)
(cond ((not (eq? p pwd)) (lambda (a) "Incorrect password"))
((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
(else (error "Unknown request -- MAKE-ACCOUNT"
m))))
dispatch)
(define acc (make-account 100 'foo))
((acc 'foo 'withdraw) 40) ;; => 60
((acc 'bar 'withdraw) 40) ;; => "Incorrect password"Exercise:
Modify the
make-accountprocedure of Exercise 3-3 by adding another local state variable so that, if an account is accessed more than seven consecutive times with an incorrect password, it invokes the procedurecall-the-cops.
Answer:
(define (call-the-cops)
"Calling the cops!")
(define (make-account balance pwd)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(let ((counter 0))
(define (dispatch p m)
(if (not (eq? p pwd))
(begin (set! counter (+ counter 1))
(cond ((> counter 7)
(call-the-cops)
(lambda (a) "We called the cops"))
(else (lambda (a) "Incorrect password"))))
(begin (set! counter 0)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
(else (error "Unknown request -- MAKE-ACCOUNT"
m))))))
dispatch))
(define acc (make-account 100 'foo))
((acc 'foo 'withdraw) 59) ;; => 41
((acc 'fo 'withdraw) 59) ;; => "Incorrect password"
((acc 'fo 'withdraw) 59) ;; => "Incorrect password"
((acc 'fo 'withdraw) 59) ;; => "Incorrect password"
((acc 'fo 'withdraw) 59) ;; => "Incorrect password"
((acc 'fo 'withdraw) 59) ;; => "Incorrect password"
((acc 'fo 'withdraw) 59) ;; => "Incorrect password"
((acc 'fo 'withdraw) 59) ;; => "Incorrect password"
((acc 'fo 'withdraw) 59) ;; => "We called the cops"
((acc 'fo 'withdraw) 59) ;; => "We called the cops"
((acc 'fo 'withdraw) 59) ;; => "We called the cops"
((acc 'foo 'withdraw) 40) ;; => 1Exercise:
It is useful to be able to reset a random-number generator to produce a sequence starting from a given value. Design a new
randprocedure that is called with an argument that is either the symbolgenerateor the symbolresetand behaves as follows:(rand 'generate)produces a new random number;((rand 'reset) <NEW-VALUE>)resets the internal state variable to the designated <NEW-VALUE>. Thus, by resetting the state, one can generate repeatable sequences. These are very handy to have when testing and debugging programs that use random numbers.
Answer:
;; mock rand-update
(define (rand-update x)
(+ x 1))
(define random-init 1)
(define rand
(let ((val random-init))
(lambda (s)
(cond ((eq? s 'generate)
(set! val (rand-update val))
val)
((eq? s 'reset)
(lambda (new-val) (set! val new-val)))
(else (error "Unknown symbol"))))))
(rand 'generate) ;; => 2
(rand 'generate) ;; => 3
(rand 'generate) ;; => 4
(rand 'generate) ;; => 5
((rand 'reset) 15)
(rand 'generate) ;; => 16
(rand 'generate) ;; => 17
(rand 'generate) ;; => 18
(rand 'generate) ;; => 19Exercise:
Consider the bank account objects created by
make-account, with the password modification described in *NoteExercise 3-3. Suppose that our banking system requires the ability to make joint accounts. Define a proceduremake-jointthat accomplishes this.Make-jointshould take three arguments. The first is a password-protected account. The second argument must match the password with which the account was defined in order for themake-jointoperation to proceed. The third argument is a new password.Make-jointis to create an additional access to the original account using the new password. For example, ifpeter-accis a bank account with passwordopen-sesame, then(define paul-acc (make-joint peter-acc 'open-sesame 'rosebud))will allow one to make transactions on
peter-accusing the namepaul-accand the passwordrosebud. You may wish to modify your solution to *Note Exercise 3-3 to accommodate this new feature.
Answer:
;; So:
;;(make-joint peter-acc 'open-sesame 'rosebud)
;; |
;; evaluates to
;; |
;; V
;; joint-acc
;;
;; such that
;;
;; (joint-acc 'rosebud 'withdraw)
;;
;; will perform the same operation performed by
;;
;; (peter-acc 'open-sesame 'withdraw)
;; So, this should work:
(define (make-joint orig-acc 'orig-pwd 'pwd)
(define (wrapper p m)
(if (eq? p pwd)
(orig-acc 'orig-pwd m)
(lambda (a) "wrong password")))
wrapper)Exercise:
When we defined the evaluation model in section *Note 1-1-3, we said that the first step in evaluating an expression is to evaluate its subexpressions. But we never specified the order in which the subexpressions should be evaluated (e.g., left to right or right to left). When we introduce assignment, the order in which the arguments to a procedure are evaluated can make a difference to the result. Define a simple procedure
fsuch that evaluating(+ (f 0) (f 1))will return 0 if the arguments to+are evaluated from left to right but will return 1 if the arguments are evaluated from right to left.
Answer:
(define f
(let ((to-return 0))
(lambda (x)
(define tmp to-return)
(set! to-return x)
tmp)))Here I’m using let to establish an environment with a local variable
to-return, bound to the initial value 0. Each time f is applied to
a value foo, f is evaluates to the value currently stored in
to-return and updates the value stored in to-return, by setting it
to foo.
Exercise:
In section *Note 1-2-1 we used the substitution model to analyze two procedures for computing factorials, a recursive version
(define (factorial n) (if (= n 1) 1 (* n (factorial (- n 1)))))and an iterative version
(define (factorial n) (fact-iter 1 1 n)) (define (fact-iter product counter max-count) (if (> counter max-count) product (fact-iter (* counter product) (+ counter 1) max-count)))Show the environment structures created by evaluating
(factorial 6)using each version of the `factorial’ procedure.
Answer:
Recursive version:
+------------------------------------------------------------------------------------+
global -->| |
env +------------------------------------------------------------------------------------+
^ ^ ^ ^ ^ ^
(factorial 6) | | | | | |
+------+ +------+ +------+ +------+ +------+ +------+
E1 ->| n: 6 | E2 ->| n: 5 | E3 ->| n: 4 | E4 -->| n: 3 | E5 ->| n: 2 | E6 -->| n: 1 |
| | | | | | | | | | | |
+------+ +------+ +------+ +------+ +------+ +------+
(if (= n 1)
1 same same same same same
(* n factorial (- n 1)))
Iterative version:
+----------------------------------------------------------------------------------------------------------------------------------------------------------------+
global -->| |
env +----------------------------------------------------------------------------------------------------------------------------------------------------------------+
^ ^ ^ ^ ^ ^ ^ ^
(factorial 6) | | | | | | | |
+------+ +-------------+ +-------------+ +-------------+ +-------------+ +--------------+ +--------------+ +--------------+
E1 ->| n: 6 | E2 ->| product: 1 | E3 ->| product: 1 | E4 ->| product: 2 | E5 ->| product: 6 | E5 ->| product: 24 | E5 ->| product: 120 | E5 ->| product: 720 |
| | | counter: 1 | | counter: 2 | | counter: 3 | | counter: 4 | | counter: 5 | | counter: 6 | | counter: 7 |
| | | max-count: 6| | max-count: 6| | max-count: 6| | max-count: 6| | max-count: 6 | | max-count: 6 | | max-count: 6 |
+------+ +-------------+ +-------------+ +-------------+ +-------------+ +--------------+ +--------------+ +--------------+
(fact-iter 1 1 n) (if (> counter max-count) same same same same same same
product
(fact-iter (* counter product)
(+ counter 1)
max-count))
Exercise:
In the
make-withdrawprocedure, the local variablebalanceis created as a parameter ofmake-withdraw. We could also create the local state variable explicitly, usinglet, as follows:(define (make-withdraw initial-amount) (let ((balance initial-amount)) (lambda (amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds"))))Recall from section *Note 1-3-2 that
letis simply syntactic sugar for a procedure call:(let ((<VAR> <EXP>)) <BODY>)is interpreted as an alternate syntax for
((lambda (<VAR>) <BODY>) <EXP>)Use the environment model to analyze this alternate version of
make-withdraw, drawing figures like the ones above to illustrate the interactions(define W1 (make-withdraw 100)) (W1 50) (define W2 (make-withdraw 100))Show that the two versions of
make-withdrawcreate objects with the same behavior. How do the environment structures differ for the two versions?
Answer:
Environments created by evaluating (define w1 (make-withdraw 100)):
GLOBAL ENV
+---------------------------------------------------------------------------------------------------------+
| make-withdraw:---+ w1:---+ |
| | | |
| | | |
| | +------------+ |
| | | |
| | | |
+------------------+------------+-------------------------------------------------------------------------+
| ↑ | E1
+----------------+ | | +----------------------+
| | | | initial-amout: 100 |
↓ | | | |
+-+-+---+ | | | |
| | +--------------+ | +----------------------+
+-+-+---+ | ↑ ↑
↓ | | |
λ | | |
| +---+---+ | |
| | | +--+ |
| +-+-+---+ |
| ↓ |
| λ |
| |
| |
| |
| |
| E2 |
| +-----------------+-----+
| | balance: 100 |
| | |
| | |
| +-----------------------+
| ↑ ↑
| | |
| | |
| +---+---+ | |
+-----→| | +--+ |
+-+-+---+ |
↓ |
λ |
|
|
|
|
|
E3 |
+-----------------+------+
| amount: 50 |
| |
| |
+------------------------+
After the evaluation:
GLOBAL ENV
+---------------------------------------------------------------------------------------------------------+
| make-withdraw:---+ w1:---+ |
| | | |
| | | |
| | +------------+ |
| | | |
| | | |
+------------------+------------+-------------------------------------------------------------------------+
| ↑ | E1
+----------------+ | | +----------------------+
| | | | initial-amout: 100 |
↓ | | | |
+-+-+---+ | | | |
| | +--------------+ | +----------------------+
+-+-+---+ | ↑ ↑
↓ | | |
λ | | |
| +---+---+ | |
| | | +--+ |
| +-+-+---+ |
| ↓ |
| λ |
| |
| |
| |
| |
| E2 |
| +-----------------+-----+
| | balance: 50 |
| | |
| | |
| +-----------------------+
| ↑
| |
| |
| +---+---+ |
+-----→| | +--+
+-+-+---+
↓
λ
Evaluating (define w2 (make-withdraw 100)):
GLOBAL ENV
+---------------------------------------------------------------------------------------------------------+
| make-withdraw:---+ w1:---+ w2:---+ |
| | | | |
| | | | |
| | +------------+ +----------+ |
| | | | |
| | | | |
+------------------+------------+------------------------------------------+------------------------------+
| ↑ | E1 | E4
+----------------+ | | +----------------------+ | +----------------------+
| | | | initial-amout: 100 | | | initial-amout: 100 |
↓ | | | | | | |
+-+-+---+ | | | | | | |
| | +--------------+ | +----------------------+ | +----------------------+
+-+-+---+ | ↑ ↑ | ↑ ↑
↓ | | | | | |
λ | | | | | |
| +---+---+ | | | +---+---+ | |
| | | +--+ | | | | +--+ |
| +-+-+---+ | | +-+-+---+ |
| ↓ | | | |
| λ ←-------------+---------------+---------+ |
| | | |
| | | |
| | | |
| | | |
| E2 | | E5 |
| +-----------------+-----+ | +-----------------+-----+
| | balance: 50 | | | balance: 100 |
| | | | | |
| | | | | |
| +-----------------------+ | +-----------------------+
| ↑ | ↑
| | | |
| | | |
| +---+---+ | | +---+---+ |
+-----→| | +--+ +------→| | +-+
+-+-+---+ +-+-+---+
↓ |
λ←--------------------------------------+
The environment structures of the two versions of make-withdraw
differ in that the second version creates one frame more than the
first version. That’s the frame holding the initial-amount binding.
Exercise:
In section 3.2.3 we saw how the environment model described the behavior of procedures with local state. Now we have seen how internal definitions work. A typical message-passing procedure contains both of these aspects. Consider the bank account procedure of section *Note 3.1.1:
(define (make-account balance) (define (withdraw amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")) (define (deposit amount) (set! balance (+ balance amount)) balance) (define (dispatch m) (cond ((eq? m 'withdraw) withdraw) ((eq? m 'deposit) deposit) (else (error "Unknown request -- MAKE-ACCOUNT" m)))) dispatch)Show the environment structure generated by the sequence of interactions
(define acc (make-account 50)) ((acc 'deposit) 40) 90 ((acc 'withdraw) 60) 30Where is the local state for
acckept? Suppose we define another account(define acc2 (make-account 100))How are the local states for the two accounts kept distinct? Which parts of the environment structure are shared between
accandacc2?
Answer:
global env
+---------------------------------------------------------------------------------------------------------+
| make-account:---+ acc:-------------------------------------------------------------+ |
| | | |
| | | |
| | | |
| | | |
| | | |
+------------------+-----------------------------------------------------------------------------------+--+
| ↑ |
+----------------+ | |
| | +-------------------------------------------------------------+ |
↓ | | balance: 50 withdraw:. deposit:. dispatch:. | |
+---+---+ | | | | | | |
| | |--------------+ | | | | | |
+-+-+---+ | | ---------+ | | |
↓ |+----------------------+ | | | |
λ || | | | |
|| | | | |
++------------------------+--------------------+--------------- |
| ↑ ↑ ↑ | | ↑ ↑ | ↑ |
+-+ | | | | | | | | | |
| | | | | | | | +--+ +--+------------+
| | | | | | | | | | |
↓ | | | ↓ | | | ↓ ↓ |
+---+---+ | | +---+---+ | | +---+---+
| | | | | | | | | | | | |
+---+---+ | | +---+---+ | | +---+---+
↓ | | ↓ | | ↓
λ | | λ | | λ
| | +--------+ |
| | | |
+----------+-------+ | | +----------+-------+
|m: 'deposit | | | |amount: 40 |
| | | | | |
| | | | | |
+------------------+ | | +------------------+
| |
| |
+-----------+ +------------+
| |
+--------+---------+ +---------+--------+
|m: 'withdraw | |amount: 60 |
| | | |
| | | |
+------------------+ +------------------+
The local state for acc is kept in the frame created by calling
make-account. If we define another account with (define acc2
(make-account 100)), then the local states for the two accounts are
kept distinct, because each call to make-account creates a frame (and
that is the frame where, as we we have seen, we keep the local state
of an account).
acc and acc2 share the text of the procedure objects widthdraw,
deposit, and dispatch.
Exercise: The following procedure for appending lists was introduced in section 2-2-1:
(define (append x y) (if (null? x) y (cons (car x) (append (cdr x) y))))
Appendforms a new list by successivelycons-ing the elements ofxontoy. The procedureappend!is similar toappend, but it is a mutator rather than a constructor. It appends the lists by splicing them together, modifying the final pair ofxso that itscdris nowy. (It is an error to callappend!with an emptyx.)(define (append! x y) (set-cdr! (last-pair x) y) x)Here
last-pairis a procedure that returns the last pair in its argument:(define (last-pair x) (if (null? (cdr x)) x (last-pair (cdr x))))Consider the interaction
(define x (list 'a 'b)) (define y (list 'c 'd)) (define z (append x y)) z (a b c d) (cdr x) <RESPONSE> (define w (append! x y)) w (a b c d) (cdr x) <RESPONSE>What are the missing <RESPONSE>s? Draw box-and-pointer diagrams to explain your answer.
Answer:
First response: ‘(b)
Box-and-pointer diagram representing the situation after evaluating (define z (append x y)):
x-->[·|·]-->[·|/]
| |
v v
a b
^ ^
| |
z-->[·|·]-->[·|·]
|
v
y-->[·|·]-->[·|/]
| |
v v
c d
Second response: ‘(b c d)
Box-and-pointer diagram representing the situation after evaluating (define w (append! x y))
w-->x-->[·|·]-->[·|·|]
| | |
v v |
a b |
v
y-->[·|·]-->[·|/]
| |
v v
c d
Exercise:
Consider the following make-cycle procedure, which uses the
last-pair procedure defined in Exercise 3-12.
(define (make-cycle x)
(set-cdr! (last-pair x) x)
x)Draw a box-and-pointer diagram that shows the structure `z’ created by
(define z (make-cycle (list ‘a ‘b ‘c)))
What happens if we try to compute `(last-pair z)’?
Answer:
Diagram:
-----> z-->[·|·]-->[·|·]-->[·|·]--
| \
----\ |
| /
---\ -------/
\-- --------/
\----/
Evaluating (last-pair z) should initiate an infinite evaluation
because the condition in last-pair will never be false.
If I evaluate the corresponding expression in Emacs, an
excessive-lisp-nesting error is displayed.
Exercise:
The following procedure is quite useful, although obscure:
(define (mystery x)
(define (loop x y)
(if (null? x)
y
(let ((temp (cdr x)))
(set-cdr! x y)
(loop temp x))))
(loop x '()))Loop uses the “temporary” variable temp to hold the old value of
the cdr of x, since the set-cdr! on the next line destroys the
cdr. Explain what mystery does in general. Suppose v is
defined by (define v (list a 'b 'c 'd)). Draw the box-and-pointer
diagram that represents the list to which v is bound. Suppose that
we now evaluate (define w (mystery v)). Draw box-and-pointer
diagrams that show the structures v and w after evaluating this
expression. What would be printed as the values of v and w?
Answer:
Mystery reverses a list.
Diagram showing what v is bound to:
v-->[·|·]-->[·|·]-->[·|·]-->[·|/]
| | | |
v v v v
a b c d
Diagram showing the structure of v and w after evaluating (define
w (mystery v)):
v
|
↓
w-->[·|·]-->[·|·]-->[·|·]-->[·|/]
| | | |
v v v v
d c b a
Exercise:
Draw box-and-pointer diagrams to explain the effect of
set-to-wow!on the structuresz1andz2above.
Answer:
z1 before:
+---+---+
z1 -->| * | * |
+-|-+-|-+
V V
+---+---+ +---+---+
x -->| * | *-+---->| * | / |
+-|-+---+ +-|-+---+
V V
+---+ +---+
| a | | b |
+---+ +---+
z1 after:
+---+---+
z1 -->| * | * |
+-|-+-|-+
V V
+---+---+ +---+---+
x -->| * | *-+---->| * | / |
+-|-+---+ +-|-+---+
V V
+---+ +---+
|wow| | b |
+---+ +---+
z2 before:
+---+---+ +---+---+ +---+---+
z2 -->| * | *-+---->| * | *-+---->| * | / |
+-|-+---+ +-|-+---+ +-|-+---+
| V V
| +---+ +---+
| | a | | b |
| +---+ +---+
| ^ ^
| | |
| +-|-+---+ +-|-+---+
+---------->| * | *-+---->| * | / |
+---+---+ +---+---+
z2 after:
+---+---+ +---+---+ +---+---+
z2 -->| * | *-+---->| * | *-+---->| * | / |
+-|-+---+ +-|-+---+ +-|-+---+
| V V
| +---+ +---+
| | a | | b |
| +---+ +---+
| ^
| |
| +---+---+ +-|-+---+
+---------->| * | *-+---->| * | / |
+-|-+---+ +---+---+
V
+---+
|wow|
+---+
Exercise:
Ben Bitdiddle decides to write a procedure to count the number of
pairs in any list structure. “It’s easy,” he reasons. “The number of
pairs in any structure is the number in the car plus the number in
the cdr plus one more to count the current pair.” So Ben writes the
following procedure:
(define (count-pairs x)
(if (not (pair? x))
0
(+ (count-pairs (car x))
(count-pairs (cdr x))
1)))Show that this procedure is not correct. In particular, draw box-and-pointer diagrams representing list structures made up of exactly three pairs for which Ben’s procedure would return 3; return 4; return 7; never return at all.
Answer:
List structure for which Ben’s procedure would return 3:
(list 1 2 3)List structure for which Ben’s procedure would return 4:
(define x (list 2))
(define y (cons x x))
(define z (cons 1 y))List structure for which Ben’s procedure would return 7:
(define x (list 2))
(define y (cons x x))
(define z (cons y y))List structure for which Ben’s procedure would never return:
;; cf. ex. 3.13
(define (last-pair x)
(if (null? (cdr x))
x
(last-pair (cdr x))))
(define (make-cycle x)
(set-cdr! (last-pair x) x)
x)
(define x (list 1 2 3))
(make-cycle x)
;; trying to count the pairs of x would never stopExercise:
Devise a correct version of the
count-pairsprocedure of Exercise 3-16 that returns the number of distinct pairs in any structure. (Hint: Traverse the structure, maintaining an auxiliary data structure that is used to keep track of which pairs have already been counted.)
;; return #t if el is in seq, false otherwise
(define (find el seq)
(cond ((null? seq) #f)
((eq? (car seq) el) #t)
(else (find el (cdr seq)))))
;; list in which we store the references of those pairs we have
;; already taken into account
(define checked '())
(define (gp/count-pairs x)
(if (not (pair? x))
0
(if (not (find x checked))
(begin
(set! checked (cons x checked))
(+ (gp/count-pairs (car x))
(gp/count-pairs (cdr x))
1))
0)))Exercise:
Write a procedure that examines a list and determines whether it contains a cycle, that is, whether a program that tried to find the end of the list by taking successive
cdr’s would go into an infinite loop. Exercise 3-13 constructed such lists.
Answer:
(define (last-pair x)
(if (null? (cdr x))
x
(last-pair (cdr x))))
(define (make-cycle x)
(set-cdr! (last-pair x) x)
x)
(define z (make-cycle (list 1 2 3)))
(define (is-cycle x)
(let ((checked '()))
(define (traverse y)
(cond ((null? y) #f)
((includes? checked (cdr y)) #t)
(else
(set! checked (cons y checked))
(traverse (cdr y)))))
(traverse x)))
(is-cycle '(1 2 3)) ;; => #f
(is-cycle z) ;; => #t
(define (make-cycle2 x)
(set-cdr! (last-pair x) x)
(cdr x))
(define foo '(1 2 3 4 5))
(is-cycle2 foo) ;; => #f
(make-cycle2 foo)
(is-cycle2 foo) ;; => #tExercise:
Ben Bitdiddle decides to test the queue implementation described above. He types in the procedures to the Lisp interpreter and proceeds to try them out:
(define q1 (make-queue)) (insert-queue! q1 'a) ((a) a) (insert-queue! q1 'b) ((a b) b) (delete-queue! q1) ((b) b) (delete-queue! q1) (() b)“It’s all wrong!” he complains. “The interpreter’s response shows that the last item is inserted into the queue twice. And when I delete both items, the second
bis still there, so the queue isn’t empty, even though it’s supposed to be.” Eva Lu Ator suggests that Ben has misunderstood what is happening. “It’s not that the items are going into the queue twice,” she explains. “It’s just that the standard Lisp printer doesn’t know how to make sense of the queue representation. If you want to see the queue printed correctly, you’ll have to define your own print procedure for queues.” Explain what Eva Lu is talking about. In particular, show why Ben’s examples produce the printed results that they do. Define a procedureprint-queuethat takes a queue as input and prints the sequence of items in the queue.
Answer:
The interpreter is printing the structures qua lists, not qua
queues. Such lists represent queues only because we have established a
convention according to which a queue is represented by a pair whose
car points to a simple list of elements and whose cdr points to
the last element of the same list the car points to. The interpreter
just prints that pair as if it was a normal pair.
The following creates a list whose car is a list which contains 'a
only and whose cdr is that list too.
(define q1 (make-queue))
(insert-queue! q1 'a)So ((a) a) is exactly what we would expect the interpreter to
print. Mutatis mutandis for structures created by (insert-queue! q1
'b), (delete-queue! q1), and (delete-queue! q1).
To print the queue we can simply print the “ordinary list” the front pointer is pointing at:
(define (print-queue queue)
(display (front-ptr queue)))Exercise:
Instead of representing a queue as a pair of pointers, we can build a queue as a procedure with local state. The local state will consist of pointers to the beginning and the end of an ordinary list. Thus, the `make-queue’ procedure will have the form
(define (make-queue) (let ((front-ptr ... ) (rear-ptr ... )) <DEFINITIONS OF INTERNAL PROCEDURES> (define (dispatch m) ...) dispatch))Complete the definition of
make-queueand provide implementations of the queue operations using this representation.
Answer:
(define (make-queue)
(let ((front-ptr nil)
(rear-ptr nil))
(define (dispatch m)
(cond ((eq? m 'empty-queue?) (null? front-ptr))
((eq? m 'front-queue)
(cond ((null? front-ptr)
(error "FRONT called with an empty queue"))
(else (car front-ptr))))
((eq? m 'insert-queue) (lambda (item)
(let ((new-pair (cons item '())))
(cond ((null? front-ptr)
(set! front-ptr new-pair)
(set! rear-ptr new-pair)
front-ptr)
(else
(set-cdr! rear-ptr new-pair)
(set! rear-ptr new-pair)
front-ptr)))))
((eq? m 'delete-queue)
(cond ((null? front-ptr)
(error "DELETE! called with an empty queue"))
(else
(set! front-ptr (cdr front-ptr))
front-ptr)))
(else (error "unknown request sorry (at least for now)"))))
dispatch))
(define queue (make-queue))
(queue 'empty-queue?) ;; => #t
((queue 'insert-queue) 'hello) ;; => (hello)
(queue 'empty-queue?) ;; => #f
(queue 'front-queue) ;; => hello
((queue 'insert-queue) 'world) ;; => (hello world)
(queue 'empty-queue?) ;; => #f
(queue 'front-queue) ;; => hello
(queue 'delete-queue) ;; => (world)
(queue 'front-queue) ;; => world
(queue 'delete-queue) ;; ()
(queue 'empty-queue?) ;; #tIn Elisp:
;; -*- lexical-binding: t -*-
(defun make-queue ()
(let ((front-ptr nil)
(rear-ptr nil))
(lambda (m)
(cond ((eq m 'empty-queue) (null front-ptr))
((eq m 'front-queue)
(cond ((null front-ptr)
(error "FRONT called with an empty queue"))
(t (car front-ptr))))
((eq m 'insert-queue) (lambda (item)
(let ((new-pair (cons item '())))
(cond ((null front-ptr)
(setq front-ptr new-pair)
(setq rear-ptr new-pair)
front-ptr)
(t
(setcdr rear-ptr new-pair)
(setq rear-ptr new-pair)
front-ptr)))))
((eq m 'delete-queue)
(cond ((null front-ptr)
(error "DELETE! called with an empty queue"))
(t
(setq front-ptr (cdr front-ptr))
front-ptr)))
(t (error "unknown request sorry (at least for now)"))))))
(let ((queue (make-queue)))
(message "Queue initially empty: %s" (funcall queue 'empty-queue)) ;; => t
(funcall (funcall queue 'insert-queue) 'hello) ;; => (hello)
(message "Queue empty after insertion: %s" (funcall queue 'empty-queue)) ;; => nil
(message "Front of queue: %s" (funcall queue 'front-queue)) ;; => hello
(funcall (funcall queue 'insert-queue) 'world) ;; => (hello world)
(funcall queue 'delete-queue) ;; => (world)
(message "Front of queue after deletion: %s" (funcall queue 'front-queue)) ;; => world
(funcall queue 'delete-queue) ;; => nil
(message "Queue empty after all deletions: %s" (funcall queue 'empty-queue)) ;; => t
)Exercise:
A “deque” (“double-ended queue”) is a sequence in which items can be inserted and deleted at either the front or the rear. Operations on deques are the constructor
make-deque, the predicateempty-deque?, selectorsfront-dequeandrear-deque, and mutatorsfront-insert-deque!,rear-insert-deque!,front-delete-deque!, andrear-delete-deque!. Show how to represent deques using pairs, and give implementations of the operations.(2) All operations should be accomplished in [theta](1) steps.
Answer:
Here is the way the structure of my deque’s implementation looks like:
+---+---+
deque -->| * | *-+---------------------------+
+-|-+---+ |
| |
| front-ptr | rear-ptr
V V
+---+---+ +---+---+ +---+---+
| * | *-+------->| * | *-+------->| * | / |
+-|-+---+ +-|-+---+ +-|-+---+
| ^______ | ^______ |
V \ V \ V
+---+---+ \ +---+---+ \ +---+---+
| \ | * + \-|-* | * | \-|-* | * |
+---+-|-+ +---+-|-+ +---+-|-+
V V V
'a 'b 'c
Basically, instead of having a head-and-tail pointer for a list of
values, like in the queue’s case, we have a head-and-tail pointer for
a list of pairs, each of which holds (in the car) a pointer to the
previous pair and (in the cdr) a value. This is one way in which we
can use pairs to build a so-called doubly-linked lists.
Here is the scheme:
(define (make-deque)
(let ((front-ptr nil)
(rear-ptr nil))
(define (dispatch m)
(cond ((eq? m 'empty-deque?) (null? front-ptr))
((eq? m 'front-deque)
(cond ((null? front-ptr)
(error "FRONT called with an empty deque"))
(else (cdar front-ptr))))
((eq? m 'rear-deque)
(cond ((null? rear-ptr)
(error "REAR called with an empty deque"))
(else (cdar rear-ptr))))
((eq? m 'front-insert-deque!) (lambda (item)
(let ((prev-and-value-pair (cons nil item)))
(let ((new-pair (cons prev-and-value-pair front-ptr)))
(cond ((null? front-ptr)
(set! front-ptr new-pair)
(set! rear-ptr new-pair))
(else
(set-car! (car front-ptr) new-pair)
(set! front-ptr new-pair)))))))
((eq? m 'rear-insert-deque!) (lambda (item)
(let ((prev-and-value-pair (cons rear-ptr item)))
(let ((new-pair (cons prev-and-value-pair nil)))
(cond ((null? rear-ptr)
(set! front-ptr new-pair)
(set! rear-ptr new-pair))
(else
(set-cdr! rear-ptr new-pair)
(set! rear-ptr new-pair)))))))
((eq? m 'front-delete-deque!)
(cond ((null? front-ptr)
(error "DELETE! called with an empty deque"))
((eq? front-ptr rear-ptr) ;; if so there is only one el
(set! front-ptr nil)
(set! rear-ptr nil)
front-ptr)
(else
(set! front-ptr (cdr front-ptr))
(and front-ptr
(cdar front-ptr)))))
((eq? m 'rear-delete-deque!)
(cond ((null? rear-ptr)
(error "DELETE! called with an empty deque"))
((eq? front-ptr rear-ptr) ;; if so there is only one el
(set! front-ptr nil)
(set! rear-ptr nil)
rear-ptr)
(else
(set! rear-ptr (caar rear-ptr))
(and rear-ptr (cdar rear-ptr)))))))
dispatch))
(define my-deque (make-deque))
((my-deque 'front-insert-deque!) 'hello)
(my-deque 'front-deque) ;; => hello
(my-deque 'rear-deque) ;; => hello
((my-deque 'rear-insert-deque!) 'world)
(my-deque 'front-deque) ;; => hello
(my-deque 'rear-deque) ;; => world
(my-deque 'front-delete-deque!) ;; => world
(my-deque 'front-deque) ;; => world
(my-deque 'rear-deque) ;; => world
(my-deque 'rear-delete-deque!) ;; => ()
(my-deque 'front-deque) ;; error: FRONT called with an empty dequeExercise:
In the table implementations above, the keys are tested for equality using
equal?(called byassoc). This is not always the appropriate test. For instance, we might have a table with numeric keys in which we don’t need an exact match to the number we’re looking up, but only a number within some tolerance of it. Design a table constructormake-tablethat takes as an argument asame-key?procedure that will be used to test “equality” of keys.Make-tableshould return adispatchprocedure that can be used to access appropriatelookupandinsert!procedures for a local table.
Answer:
(define (make-table same-key?)
(let ((local-table (list '*table*)))
(define (assoc-mod key records)
(cond ((null? records) false)
((same-key? key (caar records)) (car records))
(else (assoc-mod key (cdr records)))))
(define (lookup key-1 key-2)
(let ((subtable (assoc-mod key-1 (cdr local-table))))
(if subtable
(let ((record (assoc-mod key-2 (cdr subtable))))
(if record
(cdr record)
false))
false)))
(define (insert! key-1 key-2 value)
(let ((subtable (assoc-mod key-1 (cdr local-table))))
(if subtable
(let ((record (assoc-mod key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! local-table
(cons (list key-1
(cons key-2 value))
(cdr local-table)))))
'ok)
(define (dispatch m)
(cond ((eq? m 'lookup-proc) lookup)
((eq? m 'insert-proc!) insert!)
(else (error "Unknown operation -- TABLE" m))))
dispatch))Exercise:
Generalizing one- and two-dimensional tables, show how to implement a table in which values are stored under an arbitrary number of keys and different values may be stored under different numbers of keys. The
lookupandinsert!procedures should take as input a list of keys used to access the table.
Answer:
(define (gp-make-table)
(list '*table*))
;; try to find record
;;
;; return pair
;;
;; if cdr of return value is nil, then record has been found, and the
;; car is the record
;;
;; if cdr of return value is not nil, then record has not been found;
;; car is the last key found, cdr is the list of keys to be added
(define (find-rec t keys)
(cond ((null? keys)
(cons t keys))
((not (pair? (cdr t)))
(cons t keys))
(else (let ((found (assoc (car keys) (cdr t))))
(cond (found
(find-rec found (cdr keys)))
(else (cons t keys)))))))
(define (to-insert keys val)
(if (= (length keys) 1)
(cons (car keys) val)
(list (car keys)
(to-insert (cdr keys) val))))
(define (lookup t keys)
(let ((found (car (find-rec t keys)))
(rest-of-keys (cdr (find-rec t keys))))
(if (null? rest-of-keys)
(cdr found)
false)))
(define (insert t keys val)
(let ((found (car (find-rec t keys)))
(rest-of-keys (cdr (find-rec t keys))))
(cond ((null? rest-of-keys)
(set-cdr! found val))
((= (length rest-of-keys) 1)
(set-cdr! found
(cons
(cons (car rest-of-keys) val)
(cdr found))))
(else
"adding subtable"
(set-cdr! found
(cons
(to-insert rest-of-keys val)
(cdr found)))))))
(define t (gp-make-table))
(insert t '(letters a) 97)
t ;; => (*table* (letters (a . 97)))
(insert t '(letters b) 98)
t ;; => (*table* (letters (b . 98) (a . 97)))
(insert t '(continents europe cities barcelona population) 1620343)
t ;; => (*table* (continents (europe (cities (barcelona (population . 1620343))))) (letters (b . 98) (a . 97)))
(lookup t '(continents europe cities barcelona population)) ;; => 1620343
(lookup t '(letters b)) ;; => 98Exercise:
To search a table as implemented above, one needs to scan through the list of records. This is basically the unordered list representation of 2-3-3. For large tables, it may be more efficient to structure the table in a different manner. Describe a table implementation where the (key, value) records are organized using a binary tree, assuming that keys can be ordered in some way (e.g., numerically or alphabetically). (Compare Exercise 2-66 of Chapter 2.)
Exercise 2.66 asked for a set of records structured as a binary tree. In terms of its interface, the solution I’ve given already satisfies the requirements for a one dimensional table. You feed a key to the lookup function, you get the record, if any.
In order to make a multi-dimensional table, we could simply allow the values of the tree (table) to be trees (subtables) themselves.
For example, here is a tree I’ve used in responding exercise 2.66:
(list->tree '( (1 "el with key 1") (2 "el with key 2") (3 "etc") (4 "foo") (6 "bar") (7 "baz")))That tree has this structure[fn::To draw the structure I’m using draw-tree]:
" [o|o]---[o|o]---[o|o]---[o|o]---[o|o]---[o|/] | | | | | | | | | | | [o|o]---[o|/] | | | | | | | | | | | | 7 "baz" | | | | | | | | | [o|o]---[o|/] | | | | | | | | | | 6 "bar" | | | | | | | [o|o]---[o|/] | | | | | | | | 4 "foo" | | | | | [o|o]---[o|/] | | | | | | 3 "etc" | | | [o|o]---[o|/] | | | | 2 "el wit..." | [o|o]---[o|/] | | 1 "el wit..." "
Given the function lookup, that tree can be used as a one
dimensional table:
(define (lookup given-key set)
(cond ((null? set) false)
((= given-key (key (entry set)))
(cadr (entry set)))
((< given-key (key (entry set)))
(lookup given-key (left-branch set)))
(else (lookup given-key (right-branch set)))))
(lookup 1 (tree)) ;; => "table el 1"If we add an entries whose value is a tree itself, then we can see that we can use this structure as a multi-dimensional table. Here, for example, I build a tree with a key 999 whose value is a tree itself. Then I retrieve the value under the keys 1 and 999:
(define tree (list->tree '( (1 "table el 1") (2 "table el 2") (3 "table el 3")
(4 "table el 4") (6 "table el 6") (7 "table el 7")
(999 ((1 "subtable el 1") () ((2 "subtable el 2") () ()))))))
;; structure of the tree:
;; [o|o]---[o|o]---[o|/]
;; | | |
;; | | [o|o]---[o|o]---[o|/]
;; | | | | |
;; | | | | [o|o]---[o|o]---[o|/]
;; | | | | | | |
;; | | | | | () ()
;; | | | | |
;; | | | | [o|o]---[o|/]
;; | | | | | |
;; | | | | 999 [o|o]---[o|o]---[o|/]
;; | | | | | | |
;; | | | | | () [o|o]---[o|o]---[o|/]
;; | | | | | | | |
;; | | | | | | () ()
;; | | | | | |
;; | | | | | [o|o]---[o|/]
;; | | | | | | |
;; | | | | | 2 "subta..."
;; | | | | |
;; | | | | [o|o]---[o|/]
;; | | | | | |
;; | | | | 1 "subtab..."
;; | | | |
;; | | | [o|o]---[o|o]---[o|/]
;; | | | | | |
;; | | | | () ()
;; | | | |
;; | | | [o|o]---[o|/]
;; | | | | |
;; | | | 6 "table..."
;; | | |
;; | | [o|o]---[o|/]
;; | | | |
;; | | 7 "table..."
;; | |
;; | [o|o]---[o|o]---[o|/]
;; | | | |
;; | | | [o|o]---[o|o]---[o|/]
;; | | | | | |
;; | | | | () ()
;; | | | |
;; | | | [o|o]---[o|/]
;; | | | | |
;; | | | 3 "table..."
;; | | |
;; | | [o|o]---[o|o]---[o|/]
;; | | | | |
;; | | | () ()
;; | | |
;; | | [o|o]---[o|/]
;; | | | |
;; | | 1 "table..."
;; | |
;; | [o|o]---[o|/]
;; | | |
;; | 2 "table..."
;; |
;; [o|o]---[o|/]
;; | |
;; 4 "table..."
(lookup 1 tree) ;; => "table el 1"
(lookup 999 tree) ;; => ((1 "subtable el 1") () ((2 "subtable el 2") () ()))
(lookup 1 (lookup 999 tree)) ;; => "subtable el 1"Answer:
This exercise was somehow particularly confusing. Looking at https://github.com/kana/sicp/blob/master/ex-3.27.md helped a lot. After having looked at kana’s solution and (beautiful diagram) I tried to redo it on my own until I got it.
Before evaluating (memo-fib 3).
+------------------------------------------------------------------------------------------------------+
global env.->| memo-fib memoize |
| | | |
+---+-------------------------+-----------------------------------------------------------------+------+
| ^ ^ | ^
+--------- | | | |
| +--------+-------+ +---+-+-+ V |
| | f: o-----------+----->| o | o | +---+-+-+
| | | +-+-+---+ | o | o |
| | | | +-+-+---+
| | | | |
| +--------+-------+ V |
| ^ p: n V
| | b: (cond ...) p: f
| | b: (let ...)
| |
| +--------+-------+
| | table: {...} |
| | |
| | |
| | |
| | |
| +----------------+
| ^
| |
+------+ |
v |
+---+--+-+
| o | | |
+-+-+----+
|
|
V
p: x
b: (let ...)
memoize is bound in the global env to a pair whose cdr is a pointer
to the global env and whose car points to param f and body
(let...).
memo-fib is bound in the global env to the value returned by the
application of memoize to a lambda expression. That value is a lambda,
therefore a procedure object, therefore a pair.
Applying memoize entails
- 1) the creation of a frame which points to the global environment
— the environment the
memoizepairs points to — and in whichfis bound to a procedure object — corresponding to the lambda expression passed tomemoize— which is a pair whose cdr points to the global env. and whose care points to paramnand body(cond ...). - 2) the evaluation of the body of
memoizewithin the frame/enviroment describe in 1).
The evaluation of the body of memoize creates a frame in which
table is bound to the value return by make-table, and evaluates a
lambda expression within it, which produces a pair whose cdr points to
the frame in which table is defined and whose car points to param
x and body (let...).
Evaluating (memo-fib 3).
+------------------------------------------------------------------------------------------------------+
global env.->| memo-fib memoize |
| | | |
+---+-------------------------+-----------------------------------------------------------------+------+
| ^ ^ ^ ^ ^ ^ | ^
+--------- | | | | | | | |
| +--------+-------+ +---+-+-+ | | | | V |
| | f: o-----------+----->| o | o | | | | | +---+-+-+
| | | +-+-+---+ | | | | | o | o |
| | | | | | | | +-+-+---+
| | | | | | | | |
| +--------+-------+ V | | | | |
| ^ p: n | | | | V
| | b: (cond ...) | | | | p: f
| | | | | | b: (let ...)
| | +------+-----+ +-------+----+ +------+-----+ +-----+------+
| +--------+-------+ | n: 3 | | n: 2 | | n: 1 | | n: 0 |
| | table: {...} | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | |<----+ +------------+ +------------+ +------------+ +------------+
| | |<--+ |
| +----------------+ | |
| ^ ^ ^ ^ | +--------------------------------------------------------------+
| | | | | +-------------------------------------------------+ |
+------+ | | | +---------------------------------------+ | |
v | | +--------------------------+ | | |
+---+--+-+ +-------------+ | | | |
| o | o | | | | | |
+-+-+----+ +------+-----+ +------+-----+ +------+-----+ +------+-----+ +------+-----+
| | x: 3 | | x: 2 | | x: 1 | | x: 0 | | x: 1 |
| | | | | | | | | | |
V | | | | | | | | | |
p: x | | | | | | | | | |
b: (let ...) +------------+ +------------+ +------------+ +------------+ +------------+
memo-fib computes the nth Fibonacci number in a number of steps
proportional to n, because memo-fib never makes the same
computation more than once.
The scheme would not work if we had simply defined memo-fib to be
(memoize fib), because, in that case, the call (memo-fib 3) would
end up calling (fib 3) which would continue in the old non-memoized
way.
- We have seen that computational objects with local state are powerful tools for modeling.
- We had to pay a price though.
- Loss of referential transparency;
- Adoption of a more intricate environment model.
The central issue lurking beneath the complexity of state, sameness, and change is that by introducing assignment we are forced to admit time into our computational models. Before we introduced assignment, all our programs were timeless, in the sense that any expression that has a value always has the same value.
Building models in terms of computational objects with local state forces us to confront time as an essential concept in programming.
We can go further in structuring computational models to match our perception of the physical world. Objects in the world do not change one at a time in sequence. Rather we perceive them as acting “concurrently” — all at once.
- Introduction of assignment has meant admitting time.
- Our programs are not timeless anymore.
- Successive evaluations of the same expression can yield different values.
- Execution of assignment statements delineate a moment in time.
- The result of an evaluation now depends:
- not only on the expression itself,
- but also on whether the evaluation occurs before or after one the moments delineated by the execution of assignment statements.
- For any event A and B:
- either A happens and then B happens,
- or B happens and then A happens,
- or A and B happen at the same time.
- Authors give an example of Peter and Paul withdrawing from an
account at the same time in which concurrency is not handled
correctly.
- “The general phenomenon illustrated here is that several processes may share a common state variable.”
- “The above example typifies the subtle bugs that can creep into concurrent programs. The root of this complexity lies in the assignments to variables that are shared among the different processes.”
- Consider two processes, each of which with three ordered
events. Respectively: (a, b, c), and (x, y, z).
- there are 20 possible orderings (See p. 303)
- Consider a parallel execution of
(set! x (* x x))and(set! x (+ x 1)).- We can do so using
parallel-execute:(define x 10) (parallel-execute (lambda () (set! x (* x x))) (lambda () (set! x (+ x 1))))
- We can do so using
- There are five possible final values for the variable
x. - If we use a serializer, though, there are only two possible final
values.
- here is how we would use a serializer:
(define x 10) (define s (make-serializer)) (parallel-execute (s (lambda () (set! x (* x x)))) (s (lambda () (set! x (+ x 1)))))
- here is how we would use a serializer:
- We can now write a safer version of
make-account:(define (make-account balance) (define (withdraw amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")) (define (deposit amount) (set! balance (+ balance amount)) balance) (let ((protected (make-serializer))) (define (dispatch m) (cond ((eq? m 'withdraw) (protected withdraw)) ((eq? m 'deposit) (protected deposit)) ((eq? m 'balance) balance) (else (error "Unknown request -- MAKE-ACCOUNT" m)))) dispatch)) - Consider this procedure which swaps the value of two accounts:
(define (exchange account1 account2) (let ((difference (- (account1 'balance) (account2 'balance)))) ((account1 'withdraw) difference) ((account2 'deposit) difference))) - “For correct behavior, we must arrange for the
exchangeprocedure to lock out any other concurrent accesses to the accounts during the entire time of the exchange.” - Authors show how to implement a serializer using a mutex (aka
lock).
(define (make-serializer) (let ((mutex (make-mutex))) (lambda (p) (define (serialized-p . args) (mutex 'acquire) (let ((val (apply p args))) (mutex 'release) val)) serialized-p))) (define (make-mutex) (let ((cell (list false))) (define (the-mutex m) (cond ((eq? m 'acquire) (if (test-and-set! cell) (the-mutex 'acquire))) ; retry ((eq? m 'release) (clear! cell)))) the-mutex)) (define (clear! cell) (set-car! cell false)) (define (test-and-set! cell) (if (car cell) true (begin (set-car! cell true) false))) - Very important detail: the `test-and-set!’ operation must be performed “atomically”. (This operation is also known as Compare And Swap, (CAS). See Fedor Pikus’ presentation: https://youtu.be/ZQFzMfHIxng?t=1028)
- Authors explain what a deadlock is.
Suppose that Peter, Paul, and Mary share a joint ank account that initially contains $100. Concurrently, Peter eposits $10, Paul withdraws $20, and Mary withdraws half the oney in the account, by executing the following commands:
Peter: (set! balance (+ balance 10)) Paul: (set! balance (- balance 20)) Mary: (set! balance (- balance (/ balance 2)))
a. List all the different possible values for `balance’ after these three transactions have been completed, assuming that the banking system forces the three processes to run sequentially in some order.
b. What are some other values that could be produced if the system allows the processes to be interleaved? Draw timing diagrams like the one in *Note Figure 3-29 to explain how these values can occur.
Answer:
| peter | peter | mary | paul | paul | mary |
| paul | mary | peter | peter | mary | paul |
| mary | paul | paul | mary | peter | peter |
|---|---|---|---|---|---|
| 110 | 110 | 50 | 80 | 80 | 50 |
| 90 | 55 | 30 | 90 | 40 | 30 |
| 45 | 35 | 40 | 45 | 50 | 40 |
Here is an example of how we could end up with 110 in the bank:
Peter Paul Bank Mary
+----------------+--------------100--------------+
| | |
| V |
| Access val: 100 |
| | |
| | V
| | Access val: 100
| | |
V | |
Access val: 100 | |
| | |
| V |
| New val: 80 |
| | V
| | New val: 50
V | |
New val: 110 | |
| V |
| Set 80 ----------->80 |
| |
| |
| V
| 50<----------Set 50
|
V
Set 110--------------------------->110
Exercise:
Which of the five possibilities in the parallel execution shown above remain if we instead serialize execution as follows:
(define x 10) (define s (make-serializer)) (parallel-execute (lambda () (set! x ((s (lambda () (* x x)))))) (s (lambda () (set! x (+ x 1)))))
Answer:
I believe there are three possibilities:
- first:
- execution of
(* x x). A100value is created but not assigned; - execution of
(set! x (+ x 1)).xis now11; - execution of
(set! x 100). x is now100;
- execution of
- second:
- execution of
(* x x). A100value is created but not assigned; - execution of
(set! x 100). x is now100; - execution of
(set! x (+ x 1)).xis now101;
- execution of
- third:
- execution of
(set! x (+ x 1)).xis now11; - execution of
(* x x). A121value is created but not assigned; - execution of
(set! x 121). x is now121;
- execution of
Exercise:
Give all possible values of `x’ that can result from executing
(define x 10) (parallel-execute (lambda () (set! x (* x x))) (lambda () (set! x (* x x x))))Which of these possibilities remain if we instead use serialized procedures:
(define x 10) (define s (make-serializer)) (parallel-execute (s (lambda () (set! x (* x x)))) (s (lambda () (set! x (* x x x)))))
Answer:
- The first λ involves three events:
- two accesses of the variable
x; let’s called them `1a’ and `1b’; - one
set!; let’s call it `1s’.
- two accesses of the variable
- The second λ involves four events:
- three accesses of the variable
x; let’s called them `2a’, `2b’, and `2c’; - one
set!; let’s call it `1s’.
- three accesses of the variable
- If we serialize, then there are only two possible sequences.
- Here is one:
- 1a; (x is accessed as 10)
- 1b; (x is accessed as 10)
- 1s; (x = 10 * 10 = 100);
- 2a; (x is accessed as 100)
- 2b; (x is accessed as 100)
- 2c; (x is accessed as 100)
- 2s; (x = 100 * 100 * 100 = 1000000)
- Here is the other:
- 2a; (x is accesses as 10)
- 2b; (x is accesses as 10)
- 2c; (x is accesses as 10)
- 2s; (x = 10 * 10 * 10 = 1000)
- 1a; (x is accesses as 1000)
- 1b; (x is accesses as 1000)
- 1s; (x = 1000 * 1000 = 1000000)
- If we don’t serialize, then, besides the two sequences above, other sequences are possible.
- Here is one:
- 1a; (x is accessed as 10)
- 2a; (x is accessed as 10)
- 1b; (x is accessed as 10)
- 1s; (x = 10 * 10 = 100)
- 2b; (x is accessed as 100)
- 2c; (x is accessed as 100)
- 2s; (x = 10 * 100 * 100 = 100000)
Exercise
Ben Bitdiddle worries that it would be better to implement the bank account as follows (where the commented line has been changed):
(define (make-account balance) (define (withdraw amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")) (define (deposit amount) (set! balance (+ balance amount)) balance) ;; continued on next page (let ((protected (make-serializer))) (define (dispatch m) (cond ((eq? m 'withdraw) (protected withdraw)) ((eq? m 'deposit) (protected deposit)) ((eq? m 'balance) ((protected (lambda () balance)))) ; serialized (else (error "Unknown request -- MAKE-ACCOUNT" m)))) dispatch))because allowing unserialized access to the bank balance can result in anomalous behavior. Do you agree? Is there any scenario that demonstrates Ben’s concern?
Answer:
The only reason I can think of why one might want to adopt Ben Bitdiddle’s implementation is the following.
Without BB’s serialization, if one attempts to access the balance, while somebody else is depositing/withdrawing, then one could get a value which is would to change immediately after. With BB’s serialization, this would not happen. (The analogous “problem” of somebody depositing/withdrawing when someone else is accessing would remained. The person accessing the value would get a value which is going to change immediately after the access.)
However, it’s far-fetched to consider that as an anomaly. As far as I can see, unserialized access to the bank balance is safe.
Exercise:
Ben Bitdiddle suggests that it’s a waste of time to create a new serialized procedure in response to every `withdraw’ and `deposit’ message. He says that `make-account’ could be changed so that the calls to `protected’ are done outside the `dispatch’ procedure. That is, an account would return the same serialized procedure (which was created at the same time as the account) each time it is asked for a withdrawal procedure.
(define (make-account balance) (define (withdraw amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")) (define (deposit amount) (set! balance (+ balance amount)) balance) (let ((protected (make-serializer))) (let ((protected-withdraw (protected withdraw)) (protected-deposit (protected deposit))) (define (dispatch m) (cond ((eq? m 'withdraw) protected-withdraw) ((eq? m 'deposit) protected-deposit) ((eq? m 'balance) balance) (else (error "Unknown request -- MAKE-ACCOUNT" m)))) dispatch)))Is this a safe change to make? In particular, is there any difference in what concurrency is allowed by these two versions of `make-account’?
The change seems safe to me. I don’t see any change in the
concurrency. The only difference is that the calls (protected
withdraw) and (protected-deposit) are done only once.
Exercise:
Suppose that the balances in three accounts start out as $10, $20, and $30, and that multiple processes run, exchanging the balances in the accounts. Argue that if the processes are run sequentially, after any number of concurrent exchanges, the account balances should be $10, $20, and $30 in some order. Draw a timing diagram like the one in Figure 3-29 to show how this condition can be violated if the exchanges are implemented using the first version of the account-exchange program in this section. On the other hand, argue that even with this `exchange’ program, the sum of the balances in the accounts will be preserved. Draw a timing diagram to show how even this condition would be violated if we did not serialize the transactions on individual accounts.
Answer:
- “Argue that if the processes are run sequentially, after any number
of concurrent exchanges, the account balances should be $10, $20,
and $30 in some order.”
An exchange just moves the value of a variable
foointo another variablebar, as well as the value ofbarinfoo. So, if any exchange is atomic (that is, cannot be be interleaved with another exchange), then the final value values of the variable involved can only change in their order - “Draw a timing diagram like the one in Figure 3-29 to show how this
condition can be violated if the exchanges are implemented using the
first version of the account-exchange program in this section.”
An example (without the diagram) is offered by Authors themselves at page 308.
Peters swaps A1 and A2, and Paul swaps A1 and A3: Peter A1 A2 A3 Paul 10 20 30 calculates diff A1/A2 (-10) calculates diff A1/A3 (-20) 30<-------------------withdraw -20 A1 10<-----deposit -20 A3 withdraw -10 A1-->40 deposit -10 A2---------->10 - “On the other hand, argue that even with this `exchange’ program,
the sum of the balances in the accounts will be preserved.”
Each exchange adds and removes the same amount to a variable and from another variable. This is enough to conclude that the sum of everything cannot change.
- “Draw a timing diagram to show how even this condition would be
violated if we did not serialize the transactions on individual
accounts”
In order to violate the condition we can reproduce the kind of situation previously presented by Authors at page 301 (interleaving the events of two withdrawals):
Peters swaps A1 and A2, and Paul swaps A1 and A3: Peter A1 A2 A3 Paul 10 20 30 calculates diff (-10) calculates diff (-20) accesses A1 (10) accesses A1 (10) computes 20 computes 30 sets A1 to 20---->20 30<--------------------sets A1 to 30 deposits -10 2---------->20 10<------deposits -20 3
Exercise:
Suppose that we implement
test-and-set!using an ordinary procedure as shown in the text, without attempting to make the operation atomic. Draw a timing diagram like the one in Figure 3-29 to demonstrate how the mutex implementation can fail by allowing two processes to acquire the mutex at the same time.
Answer:
| Peter mutex Paul | | | | | false | | | | | test: | | okay | | | | | | test: | | okay | | | | | does | | stuff | | | | does | | stuff | | | | | set------------->true | | | V true<-------------set time
- This section introduces an alternative approach (alternative to assignment) to modeling state.
- Modeling state was somehow complex.
- Where was this complexity coming from?
- Real-world world objects with local state modeled by computational objects with local variables;
- time variation in the real-world identified with time variation in the computer.
- time variation of the states of the model objects in the computer implemented with assignment to the local variables in the model objects.
- “Can we avoid identifying time in the computer with time in the modeled world?”
- “time history”
- A new data structure is introduced: streams.
- Technique of delayed evaluation.
- We can model systems that have a state without ever using assignment
or mutable data.
- No more drawbacks…
- There are, though, other difficulties…
Exercise:
Complete the following definition, which generalizes stream-map to
allow procedures that take multiple arguments, analogous to map in
section 2-2-3, footnote 12.
(define (stream-map proc . argstreams)
(if (<??> (car argstreams))
the-empty-stream
(<??>
(apply proc (map <??> argstreams))
(apply stream-map
(cons proc (map <??> argstreams))))))Answer:
AFAICS, Authors haven’t shown the implementation of the map procedure
presented in the footnote 12. Let’s implement that first. I will call
it map*.
(define (map* proc . args)
(if (null? (car args))
nil
(cons
(apply proc (map car args))
(apply map* (cons proc (map cdr args))))))Here is the stream version:
(define (stream-map proc . argstreams)
(if (stream-null? (car argstreams))
the-empty-stream
(cons-stream
(apply proc (map stream-car argstreams))
(apply stream-map
(cons proc (map stream-cdr argstreams))))))Exercise:
In order to take a closer look at delayed evaluation, we will use the following procedure, which simply returns its argument after printing it:
(define (show x) (display-line x) x)What does the interpreter print in response to evaluating each expression in the following sequence?(7)
(define x (stream-map show (stream-enumerate-interval 0 10))) (stream-ref x 5) (stream-ref x 7)
Answer:
;; relevant code
(define (stream-car stream) (car stream))
(define (stream-cdr stream) (force (cdr stream)))
(define (show x)
(display-line x)
x)
(define (display-line x)
(newline)
(display x))
(define (stream-map proc s)
(if (stream-null? s)
the-empty-stream
(cons-stream (proc (stream-car s))
(stream-map proc (stream-cdr s)))))
(define (stream-enumerate-interval low high)
(if (> low high)
the-empty-stream
(cons-stream low
(stream-enumerate-interval (+ low 1) high))))
(define (stream-ref s n)
(if (= n 0)
(stream-car s)
(stream-ref (- n 1) (stream-cdr s))))Executing (define x (stream-map show (stream-enumerate-interval 0
10))) only prints 0.
Let’s try to think why is that so.
First, (stream-enumerate-interval 0 10) evaluates to a list whose
car is 0 and whose cdr is a promise:
(0 . #<promise>)Then we apply stream-map to show and to (0 . #<promise>).
stream-map evaluates to a list whose cdr is a promise; its car is
(show (stream-car (0 . #<promise>))). This latter expression
evaluates to 0, but it also has the side effect of printing a new line
and 0.
So, when evaluating (define x (stream-map show
(stream-enumerate-interval 0 10))), the interpreter prints 0.
When we evaluate (stream-ref x 5), stream-cdr is repeatedly called
and the stream is consumed until we find the 5. Therefore, we print
all the numbers from 1 to 5 (and the whole expression evaluates to 5).
- We can use streams to represent infinite sequences.
- For example, this is the definition of the stream of positive
integers:
(define (integers-starting-from n) (cons-streams n (integers-starting-from (+ n 1)))) (define integers (integers-starting-from n))
“Our programs will never know that the entire infinite stream is not there.”
- We can now define other infinite streams based on this one, e.g.:
(define (divisible? x y) (= (remainder x y) 0)) (define no-sevens ;; streams of integers that are not divisible by 7 (stream-filter (lambda (x) (not (divisible? x 7))) integers)) (stream-ref no-sevens 100) ;; => 117
- Authors show the analog way to define the infinite streams of Fibonacci numbers.
- Authors show the method, known as the “sieve of Eratosthenes”, to construct the infinite streams of prime numbers.
integersisdefined by specifying “generating” procedures that explicitly compute the stream elements one by one. An alternative way to specify streams is to take advantage of delayed evaluation to define streams implicitly. (328)
- Here is an infinite streams of ones:
(define ones (cons-stream 1 ones))
- Consider the following operation, which uses the generalized version
of
stream-mapfrom exercise 3.50:(define (add-stream s1 s2) (stream-map + s1 s2))
- Now
integerscan be defined as follows:(define integers (cons-stream 1 (add-streams ones integers)))
- Authors show “[a]n alternative way to specify a stream.”
- Here is an infinite stream of ones
(define ones (cons-stream 1 ones))
- And here is a way to define
integers:(define (add-streams s1 s2) (stream-map + s1 s2)) (define integers (cons-stream 1 (add-streams ones integers)))
Exercise:
Without running the program, describe the elements of the stream defined by
(define s (cons-stream 1 (add-streams s s)))
Answer:
The elements of the streams are the powers of 2.
s is the the list whose car is 1 and whose cdr is the promise to
execute (add-stream s s).
Forcing the cdr of s gives us the the list whose car is 2 and
whose cdr is the promise to execute (add-stream (stream-cdr s)
(stream-cdr s)).
Forcing the cdr of the cdr of s gives us the list whose car is 4
and whose cdr…
We have seen several techniques that programmers can use to tame complexity.
So far we have used Lisp. But, as complexity grows, it will not be sufficient. To the strategies for controlling complexity we must add that of establishing new languages: metalinguistic abstraction.
Establishing new languages is a powerful strategy for controlling complexity in engineering design; we can often enhance our ability to deal with a complex problem by adopting a new language that enables us to describe (and hence to think about) the problem in a different way, using primitives, means of combination, and means of abstraction that are particularly well suited to the problem at hand.
In computer programming, not only new languages can be formulated; they can also be implemented by constructing evaluators (aka interpreters), that is, procedures that, when applied to an expression of the relevant language (the language they are evaluators of), perform the actions required to evaluate the expression.
It is no exaggeration to regard this as the most fundamental idea in programming:
The evaluator, which determines the meaning of expressions in a programming language, is just another program.
To appreciate this point is to change our images of ourselves as programmers. We come to see ourselves as designers of languages, rather than only users of languages designed by others.
In fact, we can regard almost any program as the evaluator for some language.
From a certain perspective,
the technology for coping with large-scale computer systems merges with the technology for building new computer languages, and computer science itself becomes no more (and no less) than the discipline of constructing appropriate descriptive languages.
That’s the technology this chapter explores. More precisely: the technology by which languages are established in terms of other languages. Needless to say, our evaluators will be written in Lisp. The first evaluator will be for Lisp itself (a subset of the Scheme dialect).
We are going to write in Lisp an evaluator for Lisp. There’s nothing wrong with that.
An evaluator that is written in the same language that it evaluates is said to be metacircular.
The metacircular evaluator is essentially a Scheme formulation of the environment model of evaluation described in section 3.2. (362)
The environment model of evaluation has two basic parts:
- To evaluate a combination (a compound expression other than a special form), evaluate the subexpressions and then apply the value of the operator subexpression to the values of the operand subexpressions.
- To apply a compound procedure to a set of arguments, evaluate the body of the procedure in a new environment. To construct this environment, extend the environment part of the procedure object by a frame in which the formal parameters of the procedure are bound to the arguments to which the procedure is applied.
Authors say that those two rules “describe the essence of the evaluation process.” Such a process is a cycle in which expressions which are to be evaluated in environments are reduced to procedures which are to be applied to arguments, which, in turn are reduced to other expression which are to evaluated in other environments, and so on. The process terminates when the evaluator has either to look up the value of a symbol in an environment or to apply a primitive procedure (See Figure 4.1).
I find footnote 2 quite illuminating: given that the primitive procedures are not implemented in the evaluator, Authors feel the need to note that “[t]he job of the evaluator is not to specify the primitive of the language, but rather to provide the connective tissue — the means of combination and the means of abstraction — that binds a collection of primitives to form a language.” Authors, after having said that, are more specific:
- The evaluator lets us deal with nested expressions. Consider:
(+ 1 (* 2 3)). The+procedure does not know how to deal with(* 2 3)by itself; it expects number. - The evaluator lets us use variables. Consider:
(+ x 1). The primitive procedure+does not know how to deal withx; it expects numbers. - The evaluator lets us define compound procedures.
- The evaluator provides the special forms.
The implementation of the evaluator will depend upon procedures that define the “syntax” of the expressions to be evaluated. We will use data abstraction…
“Abstract syntax”:
Each type of expression has a predicate that tests for it and an abstract means for selecting its parts.
- Primitive expressions
- Special forms
- quoted expressions
- assignments/definitions of a variable
ifexpressionslambdaexpressionsbegincond
- Combinations
*Figure 4.1:* The `eval'-`apply' cycle exposes the essence of a
computer language.
.,ad88888888baa,
_ ,d8P""" ""9888ba. _
/ .a8" ,ad88888888888a |\
/ aP' ,88888888888888888a \
/ ,8" ,88888888888888888888, \
| ,8' (888888888888888888888, |
/ ,8' `8888888888888888888888 \
| 8) `888888888888888888888, |
Procedure, | 8 "88888 Apply 8888888) | Expression
Arguments | 8 Eval `888888888888888888) | Environment
| 8) "8888888888888888 |
\ (b "88888888888888' /
| `8, 8888888888888) |
\ "8a ,888888888888) /
\ V8, d88888888888" /
_\| `8b, ,d8888888888P' _/
`V8a, ,ad8888888888P'
""88888888888888888P"
""""""""""""
[graphic by Normand Veillux, modified]
[Figure from SICP Unofficial Texinfo Format version 2.neilvandyke4 (January 10, 2007)]
“Eval is a `universal machine”’. It is a machine that takes as input a description of another machine. It becomes a simulator for the machine it takes. It’s amazing that it fits on a blackboard. (https://youtu.be/aAlR3cezPJg?t=140).
(define (eval exp env)
(cond ((self-evaluating? exp) exp)
((variable? exp) (lookup-variable-value exp env))
((quoted? exp) (text-of-quotation exp))
((assignment? exp) (eval-assignment exp env))
((definition? exp) (eval-definition exp env))
((if? exp) (eval-if exp env))
((lambda? exp)
(make-procedure (lambda-parameters exp)
(lambda-body exp)
env))
((begin? exp)
(eval-sequence (begin-actions exp) env))
((cond? exp) (eval (cond->if exp) env))
((application? exp)
(apply (eval (operator exp) env)
(list-of-values (operands exp) env)))
(else
(error "Unknown expression type -- EVAL" exp))))(define (apply procedure arguments)
(cond ((primitive-procedure? procedure)
(apply-primitive-procedure procedure arguments))
((compound-procedure? procedure)
(eval-sequence
(procedure-body procedure)
(extend-environment
(procedure-parameters procedure)
arguments
(procedure-environment procedure))))
(else
(error
"Unknown procedure type -- APPLY" procedure))))(define (list-of-values exps env)
(if (no-operands? exps)
'()
(cons (eval (first-operand exps) env)
(list-of-values (rest-operands exps) env))))(define (eval-if exp env)
(if (true? (eval (if-predicate exp) env))
(eval (if-consequent exp) env)
(eval (if-alternative exp) env)))(define (eval-sequence exps env)
(cond ((last-exp? exps) (eval (first-exp exps) env))
(else (eval (first-exp exps) env)
(eval-sequence (rest-exps exps) env))))(define (eval-assignment exp env)
(set-variable-value! (assignment-variable exp)
(eval (assignment-value exp) env)
env)
'ok)(define (eval-definition exp env)
(define-variable! (definition-variable exp)
(eval (definition-value exp) env)
env)
'ok)Exercise:
Notice that we cannot tell whether the metacircular evaluator evaluates operands from left to right or from right to left. Its evaluation order is inherited from the underlying Lisp: If the arguments to `cons’ in `list-of-values’ are evaluated from left to right, then `list-of-values’ will evaluate operands from left to right; and if the arguments to `cons’ are evaluated from right to left, then `list-of-values’ will evaluate operands from right to left.
Write a version of `list-of-values’ that evaluates operands from left to right regardless of the order of evaluation in the underlying Lisp. Also write a version of `list-of-values’ that evaluates operands from right to left.
Answer:
Looking at the solutions published online, this is the widespread approach:
;; left to right
(define (list-of-values exps env)
(if (no-operands? exps)
'()
(let ((fst (eval (first-operand exps) env)))
(cons fst
(list-of-values (rest-operands exps) env)))))
;; see, for example: https://youtu.be/eoNyHC_cM7w?list=PLVFrD1dmDdvdvWFK8brOVNL7bKHpE-9w0Analogously, but without using `let` (which is just syntactic sugar):
(define (list-of-values-left exp env)
(if (no-operands? exp)
'()
((lambda (first-value)
(cons first-value (list-of-values-left (rest-operands-exps) env)))
(eval (first-operand exps) env))))
;; found here: https://github.com/cmccloud/SICP/blob/master/exercise-4.1.scmMy solution was a bit more… complex. But it should count as valid, shouldn’t it?
(define (list-of-values exps env)
;; return exps as they are except for the nth exp which is evaluated
;; as an operand
(define (eval-nth-operand exps env n)
(cond ((no-operands? exps)
'())
((= n 0)
(cons (eval (first-operand exps) env)
(cdr exps)))
(else (cons (car exps)
(eval-nth-operand (cdr exps) env (- n 1))))))
;; iteratively call eval-nth-operand for each exp
(define (iter exps env count)
(if (= count (length exps))
exps
(iter (eval-nth-operand exps env count)
env
(+ count 1))))
(iter exps env 0))Exercise:
Louis Reasoner plans to reorder the
condclauses inevalso that the clause for procedure applications appears before the clause for assignments. He argues that this will make the interpreter more efficient: Since programs usually contain more applications than assignments, definitions, and so on, his modifiedevalwill usually check fewer clauses than the originalevalbefore identifying the type of an expression.a. What is wrong with Louis’s plan? (Hint: What will Louis’s evaluator do with the expression
(define x 3)?)b. Louis is upset that his plan didn’t work. He is willing to go to any lengths to make his evaluator recognize procedure applications before it checks for most other kinds of expressions. Help him by changing the syntax of the evaluated language so that procedure applications start with
call. For example, instead of(factorial 3)we will now have to write(call factorial 3)and instead of(+ 1 2)we will have to write(call + 1 2).
Answer:
If we do as Louis say, then, the evaluator will think that (define x
3) is an application, because (application? exp) will return
true. Given so, the evaluator will evaluate the expression
(apply (eval (operator exp) env)
(list-of-values (operands exp) env))(operator exp) evaluates to x, and (operands exp) evaluates to
the list (3).
So we have
(apply (eval x env)
(list-of-values (3) env))The problem is that x in (eval x env) will be taken as a variable
and, therefore, we will try to evaluate (lookup-variable-value x
env).
We haven’t looked at lookup-variable-value yet, but, regardless,
given that x hasn’t been defined, we shouldn’t be looking it up.
This should be enough as far as I can see:
(define (application? exp)
(tagged-list exp 'call))
(define (operator exp)
(cadr exp))
(define (operands exp)
(cddr exp))Exercise:
Rewrite `eval’ so that the dispatch is done in data-directed style. Compare this with the data-directed differentiation procedure of Exercise 2-73. (You may use the `car’ of a compound expression as the type of the expression, as is appropriate for the syntax implemented in this section.)
Answer:
I think the code would look like something like this:
(define (type-tag datum) ;; p. 176
(if (pair? datum)
(car datum)
(error "Bad tagged datum -- TYPE-TAG" datum)))
(define (contents datum) ;; p. 176
(if (pair? datum)
(cdr datum)
(error "Bad tagged datum -- CONTENTS" datum)))
(define (eval exp env)
(let ((tag (type-tag exp)))
(let ((proc (get 'eval tag))
(if proc
(apply proc (list contents env))
(error "no proc found"))))))
(put 'eval
'self-evaluating
(lambda (exp env) exp))
(put 'eval
'variable
lookup-variable-value))
;; etc.Exercise:
Recall the definitions of the special forms
andandorfrom Chapter 1:
and: The expressions are evaluated from left to right. If any expression evaluates to false, false is returned; any remaining expressions are not evaluated. If all the expressions evaluate to true values, the value of the last expression is returned. If there are no expressions then true is returned.
or: The expressions are evaluated from left to right. If any expression evaluates to a true value, that value is returned; any remaining expressions are not evaluated. If all expressions evaluate to false, or if there are no expressions, then false is returned.Install
andandoras new special forms for the evaluator by defining appropriate syntax procedures and evaluation procedureseval-andandeval-or. Alternatively, show how to implementandandoras derived expressions.
Answer:
;; syntax procedures
(define (and? exp)
(tagged-list exp 'and))
(define (or? exp)
(tagged-list exp 'and))
;; evaluation procedures
(define (eval-and exp env)
(if (null? (conjuncts exp))
true
(let ((1st-evaluated-conjunct
(eval (1st-conjunct exp) env)))
(if (false? 1st-evaluated-conjunct)
false
(let ((rest (rest-conjuncts exp)))
(if (null? rest)
1st-evaluated-conjunct
(eval-and (cons 'and rest) env)))))))
(define (eval-or exp env)
(if (null? (disjuncts exp))
false
(let ((1st-evaluated-disjunct
(eval (1st-disjunct exp) env)))
(if (true? 1st-evaluated-disjunct)
1st-evaluated-disjunct
(eval-or (cons 'or (rest-disjuncts exp)) env)))))Exercise:
Scheme allows an additional syntax for
condclauses,(<TEST> => <RECIPIENT>). If <TEST> evaluates to a true value, then <RECIPIENT> is evaluated. Its value must be a procedure of one argument; this procedure is then invoked on the value of the <TEST>, and the result is returned as the value of the `cond’ expression. For example(cond ((assoc 'b '((a 1) (b 2))) => cadr) (else false))returns 2. Modify the handling of
condso that it supports this extended syntax.
Answer:
#lang sicp
(define (tagged-list? exp tag)
(if (pair? exp)
(eq? (car exp) tag)
false))
(define (begin? exp) (tagged-list? exp 'begin))
(define (begin-actions exp) (cdr exp))
(define (last-exp? seq) (null? (cdr seq)))
(define (first-exp seq) (car seq))
(define (rest-exps seq) (cdr seq))
(define (sequence->exp seq)
(cond ((null? seq) seq)
((last-exp? seq) (first-exp seq))
(else (make-begin seq))))
(define (sequence->exp2 seq)
(cond ((null? seq) seq)
((last-exp? seq) (first-exp seq))
(else (make-begin seq))))
(define (make-begin seq) (cons 'begin seq))
(define (cond? exp) (tagged-list? exp 'cond))
(define (cond-clauses exp) (cdr exp))
(define (cond-else-clause? clause)
(eq? (cond-predicate clause) 'else))
(define (cond-predicate clause) (car clause))
(define (cond-actions clause) (cdr clause))
(define (alternative-cond-actions clause)
(list (caddr clause) (car clause)))
(define (cond->if exp)
(expand-clauses (cond-clauses exp)))
(define (make-if predicate consequent alternative)
(list 'if predicate consequent alternative))
(define (alternative-cond? exp)
(eq? (cadr exp) '=>))
(define (expand-clauses clauses)
(if (null? clauses)
'false ; no `else' clause
(let ((first (car clauses))
(rest (cdr clauses)))
(if (cond-else-clause? first)
(if (null? rest)
(if (alternative-cond? first)
(alternative-cond-actions first)
(sequence->exp (cond-actions first)))
(error "ELSE clause isn't last -- COND->IF"
clauses))
(make-if (cond-predicate first)
(if (alternative-cond? first)
(alternative-cond-actions first)
(sequence->exp (cond-actions first)))
(expand-clauses rest))))))
(cond->if
'(cond ((assoc 'b '((a 1) (b 2))) => cadr)
(else false)))
;; =>
;;(if (assoc 'b '((a 1) (b 2)))
;; (cadr (assoc 'b '((a 1) (b 2))))
;; false)Exercise:
`Let’ expressions are derived expressions, because
(let ((<VAR_1> <EXP_1>) ... (<VAR_N> <EXP_N>)) <BODY>)is equivalent to
((lambda (<VAR_1> ... <VAR_N>) <BODY>) <EXP_1> ... <EXP_N>)Implement a syntactic transformation
let->combinationthat reduces evaluatingletexpressions to evaluating combinations of the type shown above, and add the appropriate clause toevalto handleletexpressions.
Answer:
#lang sicp
(define (tagged-list? exp tag)
(if (pair? exp)
(eq? (car exp) tag)
false))
(define (let? exp) (tagged-list? exp 'let))
(define (let-vars exp)
(map car (cadr exp)))
(define (let-exps exp)
(map cadr (cadr exp)))
(define (let-body exp)
(cddr exp))
(define (let-combination exp)
(cons (cons 'lambda
(cons (let-vars exp)
(let-body exp)))
(let-exps exp)))
;; Example:
(let ((let-exp '(let ((foo (* 2 4))
(bar (* 4 6)))
(display foo)
(display bar))))
(let-combination let-exp))
;; =>
;;((lambda (foo bar)
;; ((display foo)
;; (display bar)))
;; (* 2 4) (* 4 6))
;; Modifying eval:
(define (eval exp env)
(cond ((self-evaluating? exp) exp)
((variable? exp) (lookup-variable-value exp env))
((quoted? exp) (text-of-quotation exp))
((assignment? exp) (eval-assignment exp env))
((definition? exp) (eval-definition exp env))
((if? exp) (eval-if exp env))
((lambda? exp)
(make-procedure (lambda-parameters exp)
(lambda-body exp)
env))
((begin? exp)
(eval-sequence (begin-actions exp) env))
((cond? exp) (eval (cond->if exp) env))
((let? exp) (eval (let-combination exp) env)) ;; <----------------
((application? exp)
(apply (eval (operator exp) env)
(list-of-values (operands exp) env)))
(else
(error "Unknown expression type -- EVAL" exp))))Exercise:
Let*is similar tolet, except that the bindings of theletvariables are performed sequentially from left to right, and each binding is made in an environment in which all of the preceding bindings are visible. For example(let* ((x 3) (y (+ x 2)) (z (+ x y 5))) (* x z))returns 39. Explain how a
let*expression can be rewritten as a set of nestedletexpressions, and write a procedurelet*->nested-letsthat performs this transformation. If we have already implementedlet(exercise 4-6) and we want to extend the evaluator to handlelet*, is it sufficient to add a clause toevalwhose action is(eval (let*->nested-lets exp) env)or must we explicitly expand
let*in terms of non-derived expressions?
Answer:
This is the way we can translate the example given:
(let (x 3)
(let (y (+ x 2))
(let (z (+ x y 5))
(* x z))))Here is let*->nested-lets:
(define (let*-bindings exp)
(cadr exp))
(define (let*-first-binding exp)
(car (let*-bindings exp)))
(define (let*-rest-bindings exp)
(cdr (let*-bindings exp)))
(define (let*-body exp)
(caddr exp))
(define (let*->nested-lets exp)
(cond ((null? (let*-bindings exp))
(let*-body exp))
(else (cons 'let
(list (list (let*-first-binding exp))
(let*->nested-lets
(cons 'let*
(list (let*-rest-bindings exp)
(let*-body exp)))))))))
(let*->nested-lets '(let* ((x 3)
(y (+ x 2)))
(* x y)))
;; =>
;; (let ((x 3))
;; (let ((y (+ x 2)))
;; (* x y)))
(let*->nested-lets '(let* ((x 3)
(y (+ x 2))
(z (+ x y 5)))
(* x z)))
;; =>
;; (let ((x 3))
;; (let ((y (+ x 2)))
;; (let ((z (+ x y 5)))
;; (* x z))))Adding (eval (let*->nested-lets exp) env) to eval should be
sufficient, in the same way we do for cond. Or am I missing
something?
“Named
let” is a variant ofletthat has the form
(let <VAR> <BINDINGS> <BODY>)The <BINDINGS> and <BODY> are just as in ordinary
let, except that <VAR> is bound within <BODY> to a procedure whose body is <BODY> and whose parameters are the variables in the <BINDINGS>. Thus, one can repeatedly execute the <BODY> by invoking the procedure named <VAR>. For example, the iterative Fibonacci procedure (1.2.2) can be rewritten using namedletas follows:(define (fib n) (let fib-iter ((a 1) (b 0) (count n)) (if (= count 0) b (fib-iter (+ a b) a (- count 1)))))Modify
let->combinationof Exercise 4-6 to also support namedlet.
Answer:
Basically I’m making let->combination transform the “named let”
into the fib-iter definition and call as from 1.2.2.
#lang sicp
(define (tagged-list? exp tag)
(if (pair? exp)
(eq? (car exp) tag)
false))
(define (let? exp) (tagged-list? exp 'let))
(define (let-vars exp)
(map car (cadr exp)))
(define (let-exps exp)
(map cadr (cadr exp)))
(define (let-body exp)
(cddr exp))
(define (named-let->combination exp)
(let ((nameless (cons (car exp) (cddr exp)))
(name (cadr exp)))
(cons 'begin (list (cons 'define
(cons (cons name (let-vars nameless))
(let-body nameless)))
(cons name (let-exps nameless))))))
(define (let->combination exp)
(if (not (pair? (cadr exp)))
(named-let->combination exp)
(cons (list 'lambda
(let-vars exp)
(let-body exp))
(let-exps exp))))
(let ((let-exp '(let fib-iter ((a 1) (b 0) (count n))
(if (= count 0)
b
(fib-iter (+ a b) a (- count 1))))))
(let->combination let-exp))
;; =>
;; (begin
;; (define (fib-iter a b count)
;; (if (= count 0) b (fib-iter (+ a b) a (- count 1))))
;; (fib-iter 1 0 n))Should we define fib-iter only if it hasn’t already been defined? We
could add an if:
(define (named-let->combination exp)
(let ((nameless (cons (car exp) (cddr exp)))
(name (cadr exp)))
(cons 'begin (cons
(list 'if
(list 'not name)
(cons 'define
(cons (cons name (let-vars nameless))
(let-body nameless))))
(list
(cons name (let-exps nameless)))))))
(define (let->combination exp)
(if (not (pair? (cadr exp)))
(named-let->combination exp)
(cons (list 'lambda
(let-vars exp)
(let-body exp))
(let-exps exp))))
(let ((let-exp '(let fib-iter ((a 1) (b 0) (count n))
(if (= count 0)
b
(fib-iter (+ a b) a (- count 1))))))
(let->combination let-exp))
;; =>
;; (begin
;; (if (not fib-iter)
;; (define
;; (fib-iter a b count)
;; (if (= count 0) b (fib-iter (+ a b) a (- count 1)))))
;; (fib-iter 1 0 n))Many languages support a variety of iteration constructs, such as `do’, `for’, `while’, and `until’. In Scheme, iterative processes can be expressed in terms of ordinary procedure calls, so special iteration constructs provide no essential gain in computational power. On the other hand, such constructs are often convenient. Design some iteration constructs, give examples of their use, and show how to implement them as derived expressions.Many languages support a variety of iteration constructs, such as `do’, `for’, `while’, and `until’. In Scheme, iterative processes can be expressed in terms of ordinary procedure calls, so special iteration constructs provide no essential gain in computational power. On the other hand, such constructs are often convenient. Design some iteration constructs, give examples of their use, and show how to implement them as derived expressions.
Answer:
We could design a while construct with this syntax:
(while (<operator> <operand1> <operand2>)
<body>)Here is an example:
(while (> foo 0)
(display foo)
(set! foo (- foo 1)))We have learnt that we can iterate using procedures. The while loop
above can be implement in the following way:
(define (gp-while)
(if (> foo 0)
(begin
(display foo)
(set! foo (- foo 1))
(gp-while))))
(gp-while)While->combination transforms the new while syntax into procedural
syntax:
(define (append l1 l2)
(if (null? l1)
l2
(cons (car l1) (append (cdr l1) l2))))
(define (while-cond exp)
(cadr exp))
(define (while-body exp)
(cddr exp))
(define (while->combination exp)
(list 'begin
(list 'define
(list 'gp-while)
(list 'if
(while-cond exp)
(cons
'begin
(append
(while-body exp)
(list (list 'gp-while))))))
(list 'gp-while)))
;; =>
;; (begin (define (gp-while)
;; (if (> foo 0)
;; (begin (display foo)
;; (set! foo (- foo 1))
;; (gp-while))))
;; (gp-while))Now while can be handled as a derived expression by the evaluator:
(define (eval exp env)
(cond
;; ...
((while? exp) (eval (while->combination exp) env)
;; ...
))By using data abstraction, we were able to write an
evalprocedure that is independent of the particular syntax of the language to be evaluated. To illustrate this, design and implement a new syntax for Scheme by modifying the procedures in this section, without changingevalorapply.
Answer: A couple of examples:
;; 'quotation instead of 'quote
(define (quoted? exp)
(tagged-list? exp 'quotation))
(define (text-of-quotation exp) (cadr exp))
;; (assign! <value> <exp>) instead of (set! <exp> <val>)
(define (assignment? exp)
(tagged-list? exp 'assing!))
(define (assignment-variable exp) (caddr exp))
(define (assignment-value exp) (cadr exp))Testing predicates:
(define (true? x)
(not (eq? x false)))
(define (false? x)
(eq? x false))We assume we have these two procedures:
(apply-primitive-procedure <PROC> <ARGS>)
(primitive-procedure? <PROC>)Compound procedures:
(define (make-procedure parameters body env)
(list 'procedure parameters body env))
(define (compound-procedure? p)
(tagged-list? p 'procedure))
(define (procedure-parameters p) (cadr p))
(define (procedure-body p) (caddr p))
(define (procedure-environment p) (cadddr p))Operations for manipulating environments:
(lookup-variable-value <VAR> <ENV>)
(extend-environment <VARIABLES> <VALUES> <BASE-ENV>)
(define-variable! <VAR> <VALUE> <ENV>)
(set-variable-value! <VAR> <VALUE> <ENV>)To implement these operations we represent an environment as a list of frames. The enclosing environment of an environment is the
cdrof the list. The empty environment is simply the empty list.
(define (enclosing-environment env) (cdr env))
(define (first-frame env) (car env))
(define the-empty-environment '())(define (make-frame variables values)
(cons variables values))
(define (frame-variables frame) (car frame))
(define (frame-values frame) (cdr frame))
(define (add-binding-to-frame! var val frame)
(set-car! frame (cons var (car frame)))
(set-cdr! frame (cons val (cdr frame))))(define (extend-environment vars vals base-env)
(if (= (length vars) (length vals))
(cons (make-frame vars vals) base-env)
(if (< (length vars) (length vals))
(error "Too many arguments supplied" vars vals)
(error "Too few arguments supplied" vars vals))))(define (lookup-variable-value var env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (car vars))
(car vals))
(else (scan (cdr vars) (cdr vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))(define (set-variable-value! var val env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (car vars))
(set-car! vals val))
(else (scan (cdr vars) (cdr vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable -- SET!" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))(define (define-variable! var val env)
(let ((frame (first-frame env)))
(define (scan vars vals)
(cond ((null? vars)
(add-binding-to-frame! var val frame))
((eq? var (car vars))
(set-car! vals val))
(else (scan (cdr vars) (cdr vals)))))
(scan (frame-variables frame)
(frame-values frame))))Exercise:
Instead of representing a frame as a pair of lists, we can represent a frame as a list of bindings, where each binding is a name-value pair. Rewrite the environment operations to use this alternative representation.
Answer:
Let’s remember that these are the operations presented at the beginning:
(lookup-variable-value <VAR> <ENV>)
(extend-environment <VARIABLES> <VALUES> <BASE-ENV>)
(define-variable! <VAR> <VALUE> <ENV>)
(set-variable-value! <VAR> <VALUE> <ENV>)Enclosing-environment, first-frame, and the-empty-environment
can remain the way they are. For an environment remains a list of
frames.
Make-frame, instead, has to change:
(define (make-frame variable values)
(if (null? variable) ;; assumes variable and values have the same length
nil
(cons (cons (car variable) (car values))
(make-frame (cdr variable) (cdr values)))))Not sure we need frame-variables and frame-values given our new
implementation. Let’s see
For sure, though, we need a way to add a binding to a frame. Here is one way of doing it:
(define (add-binding-to-frame! var val frame)
(set-car! frame (cons var val))
(set-cdr! frame (cons (car frame) (cdr frame))))Extend-environment can be left the way it is:
(define (extend-environment vars vals base-env)
(if (= (length vars) (length vals))
(cons (make-frame vars vals) base-env)
(if (< (length vars) (length vals))
(error "Too many arguments supplied" vars vals)
(error "Too few arguments supplied" vars vals))))Here is lookup-variable-value:
(define (lookup-variable-value var env)
(define (env-loop env)
(define (scan frame)
(cond ((null? frame)
(env-loop (enclosing-environment env)))
((eq? var (caar frame))
(cdar frame))
(else (scan (cdr frame)))))
(if (eq? env the-empty-environment)
(error "Unbound variable" var)
(scan (first-frame env))))
(env-loop env))Example:
(let ((gp-env (list (make-frame '(foo bar baz) '(1 2 3))
(make-frame '(foobaz) '(4))
(make-frame '(x y z) '(5 6 7)))))
(lookup-variable-value 'foobaz gp-env))
;; => 4Here is set-variable-value!:
(define (set-variable-value! var val env)
(define (env-loop env)
(define (scan frame)
(cond ((null? frame)
(env-loop (enclosing-environment env)))
((eq? var (caar frame))
(set-cdr! (car frame) val))
(else (scan (cdr frame)))))
(if (eq? env the-empty-environment)
(error "Unbound variable -- SET!" var)
(scan (first-frame env))))
(env-loop env))Example:
(let ((gp-env (list (make-frame '(foo bar baz) '(1 2 3))
(make-frame '(foobaz) '(4))
(make-frame '(x y z) '(5 6 7)))))
(set-variable-value! 'foobaz 'FOOBAZ gp-env)
(lookup-variable-value 'foobaz gp-env))Define-variable! was a bit more problematic.
First of all let’s notice that Authors version assumes that the enviroment is not empty. We will assume that too.
The main problem I had to solve was this: if a frame is an empty list
because there are no bindings, add-binding-to-frame! won’t work. For
neither set-car! nor set-cdr! can applied to an empty list. So, my
solution assumes that we established the convention that that an empty
frame is a list with an empty list in it.
This is an empty frame:
'(())And this is an environment with an empty frame:
'((()))Given this, here is define-variable!:
(define (define-variable! var val env)
(let ((frame (first-frame env)))
(define (scan frame)
(cond ((null? (car frame))
(set-car! frame (cons var val)))
((eq? var (caar frame))
(set-car! frame (cons var val)))
(else
(if (null? (cdr frame))
(begin
(set-car! frame '())
(scan frame))
(scan (cdr frame))))))
(scan frame)))Exercise:
The procedures `set-variable-value!’, `define-variable!’, and `lookup-variable-value’ can be expressed in terms of more abstract procedures for traversing the environment structure. Define abstractions that capture the common patterns and redefine the three procedures in terms of these abstractions.
Answer:
(define (rest-of-vars vars)
(cdr vars))
(define (rest-of-vals vals)
(cdr vals))
(define (set-first-value! vals val)
(set-car! vals val))
(define (first-var vars)
(car vars))
(define (set-variable-value! var val env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (first-var vars))
(set-first-value! vals val))
(else (scan (rest-of-vars vars) (rest-of-vals vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable -- SET!" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))
(define (lookup-variable-value var env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (first-var vars))
(car vals))
(else (scan (rest-of-vars vars) (rest-of-vals vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))
(define (define-variable! var val env)
(let ((frame (first-frame env)))
(define (scan vars vals)
(cond ((null? vars)
(add-binding-to-frame! var val frame))
((eq? var (first-var vars))
(set-first-value! vals val))
(else (scan (rest-of-vars vars) (rest-of-vals vals)))))
(scan (frame-variables frame)
(frame-values frame))))Exercise:
Scheme allows us to create new bindings for variables by means of `define’, but provides no way to get rid of bindings. Implement for the evaluator a special form `make-unbound!’ that removes the binding of a given symbol from the environment in which the `make-unbound!’ expression is evaluated. This problem is not completely specified. For example, should we remove only the binding in the first frame of the environment? Complete the specification and justify any choices you make.
I think we should remove the binding only in the first frame. If we did otherwise, then couldn’t we mutate frames other parts of the program rely on?
Given that, as far as I know, we cannot mutate a list with one
member into an empty list, I’m using an iterative-process-evolving
filter-frame procedure which construct a new list (well two new
lists, new-vars and new-vals) and then I set the car of the
environment (that is, I replace the first frame with a new one).
(define (append l1 l2)
(if (null? l1)
l2
(cons (car l1) (append (cdr l1) l2))))
;; Usage:
;; (make-unbound! 'foo)
(define (var-to-unbind exp)
(cadr exp))
(define (eval-make-unbound exp env)
(define (filter-frame vars vals var new-vars new-vals)
(cond ((null? vars)
(set-car! env (cons new-vars new-vals)))
((eq? (car vars) var)
(filter-frame nil
nil
var
(append (cdr vars) new-vars)
(append (cdr vals) new-vals)))
(else (filter-frame (cdr vars)
(cdr vals)
var
(append (list (car vars)) new-vars)
(append (list (car vals)) new-vals)))))
(filter-frame (frame-variables (first-frame env))
(frame-values (first-frame env))
(var-to-unbind exp)
nil
nil))
(define gp-env '(((a b c) 1 2 3) ((d e f) 4 5 6)))
(eval-make-unbound '(make-unbound b) gp-env)
gp-env
;; => (((c a) 3 1) ((d e f) 4 5 6))- The evaluator provides a description of the process to evaluate a Lisp expression.
- Such a description is in a programming language (Lisp), so we can run it.
- Given that evaluator “reduces expressions ultimately to the application of primitive procedures”, we need a way to use the underlying Lisp system to apply those procedures.
- The global environment, consequently, shall contain bindings for each primitive procedure name.
- The global environment shall also contain bindings for
trueandfalse.
(define (setup-environment)
(let ((initial-env
(extend-environment (primitive-procedure-names)
(primitive-procedure-objects)
the-empty-environment)))
(define-variable! 'true true initial-env)
(define-variable! 'false false initial-env)
initial-env))
(define the-global-environment (setup-environment))Primitive procedure are represented as tagged lists. This specific
representation is hidden behind the primitive-procedure? and
primitive-implementation abstractions so it could be replaced by a
different one.
(define (primitive-procedure? proc)
(tagged-list? proc 'primitive))
(define (primitive-implementation proc) (cadr proc))(define primitive-procedures
(list (list 'car car)
(list 'cdr cdr)
(list 'cons cons)
(list 'null? null?)
<MORE PRIMITIVES>
))
(define (primitive-procedure-names)
(map car
primitive-procedures))
(define (primitive-procedure-objects)
(map (lambda (proc) (list 'primitive (cadr proc)))
primitive-procedures))Here is how we apply a primitive
procedure. Apply-in-underlying-scheme is nothing more than the
apply procedures from the underlying scheme we have used in the
previous chapters.
(define (apply-primitive-procedure proc args)
(apply-in-underlying-scheme
(primitive-implementation proc) args))Authors provide what they call a “driver loop” as a convenience for running the evaluator, which “models the read-eval-print loop of the underlying Lisp system.”
(define input-prompt ";;; M-Eval input:")
(define output-prompt ";;; M-Eval value:")
(define (driver-loop)
(prompt-for-input input-prompt)
(let ((input (read)))
(let ((output (eval input the-global-environment)))
(announce-output output-prompt)
(user-print output)))
(driver-loop))
(define (prompt-for-input string)
(newline) (newline) (display string) (newline))
(define (announce-output string)
(newline) (display string) (newline))User-print is used to avoid printing the the environment part of a
compound procedure:
(define (user-print object)
(if (compound-procedure? object)
(display (list 'compound-procedure
(procedure-parameters object)
(procedure-body object)
'<procedure-env>))
(display object)))Finally:
(define the-global-environment (setup-environment))
(driver-loop)
;;; M-Eval input:
(define (append x y)
(if (null? x)
y
(cons (car x)
(append (cdr x) y))))
;;; M-Eval value:
ok
;;; M-Eval input:
(append '(a b c) '(d e f))
;;; M-Eval value:
(a b c d e f)What follows is the whole code for the evaluator presented so far. I’ve evaluated it in DrRacket and I can confirm that it works.
Notice: I’ve renamed apply into apply-evaluator. Racket would
otherwise complain about the first definition ((define
apply-in-underlying-scheme apply)), telling me that I cannot use
apply before defining it.
#lang sicp
(define apply-in-underlying-scheme apply)
(define (eval exp env)
(cond ((self-evaluating? exp) exp)
((variable? exp) (lookup-variable-value exp env))
((quoted? exp) (text-of-quotation exp))
((assignment? exp) (eval-assignment exp env))
((definition? exp) (eval-definition exp env))
((if? exp) (eval-if exp env))
((lambda? exp)
(make-procedure (lambda-parameters exp)
(lambda-body exp)
env))
((begin? exp)
(eval-sequence (begin-actions exp) env))
((cond? exp) (eval (cond->if exp) env))
((application? exp)
(apply-evaluator (eval (operator exp) env)
(list-of-values (operands exp) env)))
(else
(error "Unknown expression type -- EVAL" exp))))
(define (apply-evaluator procedure arguments)
(cond ((primitive-procedure? procedure)
(apply-primitive-procedure procedure arguments))
((compound-procedure? procedure)
(eval-sequence
(procedure-body procedure)
(extend-environment
(procedure-parameters procedure)
arguments
(procedure-environment procedure))))
(else
(error
"Unknown procedure type -- APPLY" procedure))))
(define (list-of-values exps env)
(if (no-operands? exps)
'()
(cons (eval (first-operand exps) env)
(list-of-values (rest-operands exps) env))))
(define (eval-if exp env)
(if (true? (eval (if-predicate exp) env))
(eval (if-consequent exp) env)
(eval (if-alternative exp) env)))
(define (eval-sequence exps env)
(cond ((last-exp? exps) (eval (first-exp exps) env))
(else (eval (first-exp exps) env)
(eval-sequence (rest-exps exps) env))))
(define (eval-assignment exp env)
(set-variable-value! (assignment-variable exp)
(eval (assignment-value exp) env)
env)
'ok)
(define (eval-definition exp env)
(define-variable! (definition-variable exp)
(eval (definition-value exp) env)
env)
'ok)
(define (self-evaluating? exp)
(cond ((number? exp) true)
((string? exp) true)
(else false)))
(define (variable? exp) (symbol? exp))
(define (quoted? exp)
(tagged-list? exp 'quote))
(define (text-of-quotation exp) (cadr exp))
(define (tagged-list? exp tag)
(if (pair? exp)
(eq? (car exp) tag)
false))
(define (assignment? exp)
(tagged-list? exp 'set!))
(define (assignment-variable exp) (cadr exp))
(define (assignment-value exp) (caddr exp))
(define (definition? exp)
(tagged-list? exp 'define))
(define (definition-variable exp)
(if (symbol? (cadr exp))
(cadr exp)
(caadr exp)))
(define (definition-value exp)
(if (symbol? (cadr exp))
(caddr exp)
(make-lambda (cdadr exp) ; formal parameters
(cddr exp)))) ; body
(define (lambda? exp) (tagged-list? exp 'lambda))
(define (lambda-parameters exp) (cadr exp))
(define (lambda-body exp) (cddr exp))
(define (make-lambda parameters body)
(cons 'lambda (cons parameters body)))
(define (if? exp) (tagged-list? exp 'if))
(define (if-predicate exp) (cadr exp))
(define (if-consequent exp) (caddr exp))
(define (if-alternative exp)
(if (not (null? (cdddr exp)))
(cadddr exp)
'false))
(define (make-if predicate consequent alternative)
(list 'if predicate consequent alternative))
(define (begin? exp) (tagged-list? exp 'begin))
(define (begin-actions exp) (cdr exp))
(define (last-exp? seq) (null? (cdr seq)))
(define (first-exp seq) (car seq))
(define (rest-exps seq) (cdr seq))
(define (sequence->exp seq)
(cond ((null? seq) seq)
((last-exp? seq) (first-exp seq))
(else (make-begin seq))))
(define (make-begin seq) (cons 'begin seq))
(define (application? exp) (pair? exp))
(define (operator exp) (car exp))
(define (operands exp) (cdr exp))
(define (no-operands? ops) (null? ops))
(define (first-operand ops) (car ops))
(define (rest-operands ops) (cdr ops))
(define (cond? exp) (tagged-list? exp 'cond))
(define (cond-clauses exp) (cdr exp))
(define (cond-else-clause? clause)
(eq? (cond-predicate clause) 'else))
(define (cond-predicate clause) (car clause))
(define (cond-actions clause) (cdr clause))
(define (cond->if exp)
(expand-clauses (cond-clauses exp)))
(define (expand-clauses clauses)
(if (null? clauses)
'false ; no `else' clause
(let ((first (car clauses))
(rest (cdr clauses)))
(if (cond-else-clause? first)
(if (null? rest)
(sequence->exp (cond-actions first))
(error "ELSE clause isn't last -- COND->IF"
clauses))
(make-if (cond-predicate first)
(sequence->exp (cond-actions first))
(expand-clauses rest))))))
(define (true? x)
(not (eq? x false)))
(define (false? x)
(eq? x false))
(define (make-procedure parameters body env)
(list 'procedure parameters body env))
(define (compound-procedure? p)
(tagged-list? p 'procedure))
(define (procedure-parameters p) (cadr p))
(define (procedure-body p) (caddr p))
(define (procedure-environment p) (cadddr p))
(define (enclosing-environment env) (cdr env))
(define (first-frame env) (car env))
(define the-empty-environment '())
(define (make-frame variables values)
(cons variables values))
(define (frame-variables frame) (car frame))
(define (frame-values frame) (cdr frame))
(define (add-binding-to-frame! var val frame)
(set-car! frame (cons var (car frame)))
(set-cdr! frame (cons val (cdr frame))))
(define (extend-environment vars vals base-env)
(if (= (length vars) (length vals))
(cons (make-frame vars vals) base-env)
(if (< (length vars) (length vals))
(error "Too many arguments supplied" vars vals)
(error "Too few arguments supplied" vars vals))))
(define (lookup-variable-value var env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (car vars))
(car vals))
(else (scan (cdr vars) (cdr vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))
(define (set-variable-value! var val env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (car vars))
(set-car! vals val))
(else (scan (cdr vars) (cdr vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable -- SET!" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))
(define (define-variable! var val env)
(let ((frame (first-frame env)))
(define (scan vars vals)
(cond ((null? vars)
(add-binding-to-frame! var val frame))
((eq? var (car vars))
(set-car! vals val))
(else (scan (cdr vars) (cdr vals)))))
(scan (frame-variables frame)
(frame-values frame))))
(define primitive-procedures
(list (list 'car car)
(list 'cdr cdr)
(list 'cons cons)
(list 'null? null?)
(list '+ +)
(list '- -)
(list '* *)
(list '/ /)))
(define (primitive-procedure-names)
(map car
primitive-procedures))
(define (primitive-procedure-objects)
(map (lambda (proc) (list 'primitive (cadr proc)))
primitive-procedures))
(define (setup-environment)
(let ((initial-env
(extend-environment (primitive-procedure-names)
(primitive-procedure-objects)
the-empty-environment)))
(define-variable! 'true true initial-env)
(define-variable! 'false false initial-env)
initial-env))
(define (primitive-procedure? proc)
(tagged-list? proc 'primitive))
(define (primitive-implementation proc) (cadr proc))
(define (apply-primitive-procedure proc args)
(apply-in-underlying-scheme
(primitive-implementation proc) args))
(define input-prompt ";;; M-Eval input:")
(define output-prompt ";;; M-Eval value:")
(define (driver-loop)
(prompt-for-input input-prompt)
(let ((input (read)))
(let ((output (eval input the-global-environment)))
(announce-output output-prompt)
(user-print output)))
(driver-loop))
(define (prompt-for-input string)
(newline) (newline) (display string) (newline))
(define (announce-output string)
(newline) (display string) (newline))
(define (user-print object)
(if (compound-procedure? object)
(display (list 'compound-procedure
(procedure-parameters object)
(procedure-body object)
'<procedure-env>))
(display object)))
(define the-global-environment (setup-environment))
(driver-loop)Exercise:
Eva Lu Ator and Louis Reasoner are each experimenting with the metacircular evaluator. Eva types in the definition of
map, and runs some test programs that use it. They work fine. Louis, in contrast, has installed the system version ofmapas a primitive for the metacircular evaluator. When he tries it, things go terribly wrong. Explain why Louis’smapfails even though Eva’s works.
Answer:
Apply is called in both scenarios. The arguments that apply
receives are the already-evaluated operands of the combination
(evaluated by list-of-values). I think that the problem with using
the primitive map is that one the arguments received by apply is
an entity representing a procedure using our implementation (our
implementation is a list whose car is the tag 'procedure, among
other aspects). But the primitive car expects a different kind of
procedure object (whatever Scheme natively uses).
- One operational view of the meaning of a program: a program is a description of an abstract machine. (Cf. the lecture)
- Example:
factorial. - The evaluator can be thought of as a special machine that takes as
input a description of a machine and emulates the machine whose
description it takes.
- The evaluator could, for example, take
factorialand be able to compute factorials.
- The evaluator could, for example, take
- The evaluator can, therefore, be seen as a universal machine.
- “This is striking” (386)
- “Another striking aspect of the evaluator is that it acts as a
bridge between the data objects that are manipulated by our
programming language and the programming language itself”. (386)
- “…the user’s program are the evaluator’s data…”
Exercise:
Given a one-argument procedure p and an object a, p is said to
“halt” on a if evaluating the expression (p a) returns a value (as
opposed to terminating with an error message or running forever).
Show that it is impossible to write a procedure halts? that
correctly determines whether p halts on a for any procedure p
and object a. Use the following reasoning: If you had such a
procedure halts?, you could implement the following program:
(define (run-forever) (run-forever))
(define (try p)
(if (halts? p p)
(run-forever)
'halted))Now consider evaluating the expression (try try) and show that any
possible outcome (either halting or running forever) violates the
intended behavior of halts?.[fn::Although we stipulated that
`halts?’ is given a procedure object, notice that this reasoning still
applies even if `halts?’ can gain access to the procedure’s text and
its environment. This is Turing’s celebrated “Halting Theorem”, which
gave the first clear example of a “non-computable” problem, i.e., a
well-posed task that cannot be carried out as a computational
procedure.]
Answer:
Suppose that applying try to try halts. If so, then, when calling
(try try), we will call (run-forever) and, indeed, run forever.
Suppose that applying try to try does not halt. If so, then, when
calling (try try), we would return halted.
This is the way I would put it: we have got a paradox. On the one
hand, if (try try) halts, then it doesn’t halt. On the other hand,
if (try try) does not halt, then it halts.
- Environment model of evaluation & metacircular evaluator: definition are executed “in sequence, extending the environment frame one definition at a time.”
- “This is particularly convenient for interactive program development…”
- “However, if we think carefully about the internal definitions used to implement block structure […] we will find that name-by-name extension of the environment may not be the best way to define local variables.”
- Example:
(define (f x) (define (even? n) (if (= n 0) true (odd? (- n 1)))) (define (odd? n) (if (= n 0) false (even? (- n 1)))) <REST OF BODY OF `F'>)
- “the only satisfactory interpretation of the two
define’s is to regard them as if the nameeven?andodd?were being added to the environment simultaneously.” - “More generally, in block structure, the scope of a local name is the entire procedure body in which the `define’ is evaluated.”
- “…our interpreter will evaluate calls to `f’ correctly, but for an “accidental” reason…”
- There is “a simple way to treat definitions so that internally defined names have truly simultaneous scope”…
- The procedure
(lambda <VARS> (define u <E1>) (define v <E2>) <E3>)
can be transformed into
(lambda <VARS> (let ((u '*unassigned*) (v '*unassigned*)) (set! u <E1>) (set! v <E2>) <E3>))
“where `*unassigned*’ is a special symbol that causes looking up a variable to signal an error if an attempt is made to use the value of the not-yet-assigned variable.”
- “An alternative strategy for scanning out internal definitions is shown in *Note Exercise 4-18.”
Exercise:
In this exercise we implement the method just described for interpreting internal definitions. We assume that the evaluator supports
let(See Exercise 4.6).a. Change
lookup-variable-value(Section 4.1.3) to signal an error if the value it finds is the symbol*unassigned*.b. Write a procedure
scan-out-definesthat takes a procedure body and returns an equivalent one that has no internal definitions, by making the transformation described above.c. Install
scan-out-definesin the interpreter, either inmake-procedureor inprocedure-body(section 4-1-3). Which place is better? Why?
Answer:
- a:
(define (lookup-variable-value var env) (define (env-loop env) (define (scan vars vals) (cond ((null? vars) (env-loop (enclosing-environment env))) ((eq? var (car vars)) (if (eq? (car vals) '*unassigned*) (error "not-yet-assigned variable" var) (car vals))) (else (scan (cdr vars) (cdr vals))))) (if (eq? env the-empty-environment) (error "Unbound variable" var) (let ((frame (first-frame env))) (scan (frame-variables frame) (frame-values frame))))) (env-loop env))
- b:
(define (filter pred seq) (cond ((null? seq) nil) ((pred (car seq)) (cons (car seq) (filter pred (cdr seq)))) (else (filter pred (cdr seq))))) (define (append l1 l2) (if (null? l1) l2 (cons (car l1) (append (cdr l1) l2)))) ;; example of a procedure body (define body-example '((define even? (lambda (n) (if (= n 0) true (odd? (- n 1))))) (define odd? (lambda (n) (if (= n 0) false (even? (- n 1))))) (message "hello world") (progn (* 3 3) (message "foobar")) (define another-var (* 3 2)))) ;; return a list with: ;; car (1st el): body without definitions ;; cadr (2nd el): a list of the variables ;; caddr (3rd el): a list of the values for the variables (define (gp-build-lists body body-no-defs vars vals) (cond ((null? body) (list body-no-defs vars vals)) ;; we finished scanning, return results ((eq? (caar body) 'define) (gp-build-lists (cdr body) ;; filter definition out body-no-defs ;; nothing to be addedd to new-body (we ;; want the define to be gone) (cons (cadar body) vars) ;; add var (cons (caddar body) vals))) ;; add val (else (gp-build-lists (cdr body) (append body-no-defs (list (car body))) vars vals)))) ;; map vars to lists whose car is the var and show cadr is the symbol ;; '*unassigned* (define (build-unassigned-vars vars) ;; we could use map, but I'm doing it manually (if (null? vars) nil (cons (list (car vars) '*unassigned*) (build-unassigned-vars (cdr vars))))) ;; maps vars to lists whose car is the var and whose cadr is the ;; associated val (define (build-sets vars vals) ;; we could use map, but I'm doing it manually (if (null? vars) nil (cons (list 'set! (car vars) (car vals)) (build-sets (cdr vars) (cdr vals))))) (define (scan-out-defines body) (let ((lists (gp-build-lists body nil nil nil))) (let ((body-no-defs (car lists)) (vars (cadr lists)) (vals (caddr lists))) (append (append (cons 'let (list (build-unassigned-vars vars))) (build-sets vars vals)) body-no-defs)))) ;; example: (scan-out-defines body-example) ;; => ;; (let ((another-var *unassigned*) (odd? *unassigned*) (even? *unassigned*)) ;; (set! another-var (* 3 2)) ;; (set! odd? (lambda (n) (if (= n 0) false (even? (- n 1))))) ;; (set! even? (lambda (n) (if (= n 0) true (odd? (- n 1))))) ;; (message "hello world") ;; (progn (* 3 3) (message "foobar")))
- c:
Make-procedureis used inevalto construct procedures.Procedure-bodyis used inapplyto select the bodies of procedures.I think it would be better to install
scan-out-definesinmake-procedure, rather than inprocedure-body, because we would avoid callingscan-out-definesmore than once for the same procedure (scan-out-defineswould be called for each application).(define (make-procedure parameters body env) (list 'procedure parameters (scan-out-defines body) env))
Exercise:
Draw diagrams of the environment in effect when evaluating the expression <e3> in the procedure in the text, comparing how this will be structured when definitions are interpreted sequentially with how it will be structured if definitions are scanned out as described. Why is there an extra frame in the transformed program? Explain why this difference in environment structure can never make a difference in the behavior of a correct program. Design a way to make the interpreter implement the “simultaneous” scope rule for internal definitions without constructing the extra frame.
Answer:
The following is the environment structure when definition are interpreted sequentially; <e3> is evaluated in E1.
global env
|
V
+-------------+
| ... |
| |
+-------------+
^ ^ E1
| | |
| | V
+---+-+-+ | +-------------+
| . | . | +----+ u: e1 |
+-+-+---+ | v: e2 |
| +-------------+
|
V
params: vars
body: (define u <E1>)
(define v <E2>)
<E3>
The following is the environment structure when definition are scanned out; <e3> is evaluated in E2.
global env
|
V
+-------------+
| ... |
| |
+-------------+
^ ^ E1
| | |
| | V
+---+-+-+ | +-------------+
| . | . | +-------------+ vars |
+-+-+---+ | |
| +-------------+ E2
| ^ |
V | V
params: vars | +-------------+
body: (let ((u '*unassigned*) +--+ u: e1 |
(v '*unassigned*)) | v: e2 |
(set! u <E1>) +-------------+
(set! v <E2>)
<E3>)
In the second structure there is an extra frame because a let is
equivalent to the application of a lambda, and the application of a
lambda involves the creation of a new frame.
As long as <e3> is evaluated after u is set to e1 and v to
e2 there won’t be any difference between the behaviuor in the two
environments, because there is no difference with respect to the
values of the bindings in the environment.
Simultaneous scope without an extra frame could be achieved by
transforming the body of the lambda so that all its internal
definitions come before all the rest (cf. the “accidental reason”,
Authors mention, because calls to the example procedure f work).
Exercise:
Ben Bitdiddle, Alyssa P. Hacker, and Eva Lu Ator are arguing about the desired result of evaluating the expression
(let ((a 1)) (define (f x) (define b (+ a x)) (define a 5) (+ a b)) (f 10))Ben asserts that the result should be obtained using the sequential rule for
define:bis defined to be 11, thenais defined to be 5, so the result is 16. Alyssa objects that mutual recursion requires the simultaneous scope rule for internal procedure definitions, and that it is unreasonable to treat procedure names differently from other names. Thus, she argues for the mechanism implemented Exercise 4.16. This would lead toabeing unassigned at the time that the value forbis to be computed. Hence, in Alyssa’s view the procedure should produce an error. Eva has a third opinion. She says that if the definitions ofaandbare truly meant to be simultaneous, then the value 5 forashould be used in evaluatingb. Hence, in Eva’s viewashould be 5,bshould be 15, and the result should be 20. Which (if any) of these viewpoints do you support? Can you devise a way to implement internal definitions so that they behave as Eva prefers?
Answer:
Both Ben’s approach and Alyssa’s approach seem okay to me. As far as
I can see, a serious obstacle for Eva’s approach is represented by
what we might call “interdependent definitions”. For example, what
would we be supposed to do if the definitions of b and a were the
following?
(define b (+ a x))
(define a (b + 5))I cannot see a way to follow Eva’s approach, given the possibility of this kind of situations, can I?
(
Authors say that MIT Scheme generates an error. Javascript raises an error too, when evaluating equivalent code:
((a) => {
function f(x) {
let b = a + x;
let a = 5;
return a + b;
}
f(10);
})(1)
/*
Uncaught ReferenceError: Cannot access 'a' before initialization
at f (REPL11:4:15)
at REPL11:9:5
*/)
Exercise:
Because internal definitions look sequential but are actually simultaneous, some people prefer to avoid them entirely, and use the special form
letrecinstead.Letreclooks likelet, so it is not surprising that the variables it binds are bound simultaneously and have the same scope as each other. The sample procedurefabove can be written without internal definitions, but with exactly the same meaning, as(define (f x) (letrec ((even? (lambda (n) (if (= n 0) true (odd? (- n 1))))) (odd? (lambda (n) (if (= n 0) false (even? (- n 1)))))) <rest of body of f>))
Letrecexpressions, which have the form(letrec ((<var_1> <exp_1>) ... (<var_n> <exp_n>)) <body>)are a variation on
letin which the expressions <exp_k> that provide the initial values for the variables <var_k> are evaluated in an environment that includes all theletrecbindings. This permits recursion in the bindings, such as the mutual recursion ofeven?andodd?in the example above, or the evaluation of 10 factorial with(letrec ((fact (lambda (n) (if (= n 1) 1 (* n (fact (- n 1))))))) (fact 10))a. Implement
letrecas a derived expression, by transforming aletrecexpression into aletexpression as shown in the text above or in Exercise 4.18. That is, theletrecvariables should be created with aletand then be assigned their values withset!.b. Louis Reasoner is confused by all this fuss about internal definitions. The way he sees it, if you don’t like to use
defineinside a procedure, you can just uselet. Illustrate what is loose about his reasoning by drawing an environment diagram that shows the environment in which the<rest of body of f>is evaluated during evaluation of the expression(f 5), withfdefined as in this exercise. Draw an environment diagram for the same evaluation, but withletin place ofletrecin the definition off.
Answer:
a:
(define (append l1 l2)
(if (null? l1)
l2
(cons (car l1) (append (cdr l1) l2))))
(define example-letrec
'(letrec ((even?
(lambda (n)
(if (= n 0)
true
(odd? (- n 1)))))
(odd?
(lambda (n)
(if (= n 0)
false
(even? (- n 1))))))
(message "ciao")
(message "hola")))
(define (letrec-body exp)
(cddr exp))
(define (letrec-bindings exp)
(cadr exp))
(define (letrec-vars bindings)
(if (null? bindings)
nil
(cons (caar bindings) (letrec-vars (cdr bindings)))))
(define (letrec-vals bindings)
(if (null? bindings)
nil
(cons (cadar bindings) (letrec-vals (cdr bindings)))))
(define (letrec-build-unassigned-vars vars)
(if (null? vars)
nil
(cons (list (car vars) '*unassigned*) (letrec-build-unassigned-vars (cdr vars)))))
(define (letrec-build-sets vars vals)
(if (null? vars)
nil
(cons (list 'set! (car vars) (car vals))
(letrec-build-sets (cdr vars) (cdr vals)))))
(define (letrec-to-let exp)
(append
(cons 'let (list (letrec-build-unassigned-vars (letrec-vars (letrec-bindings exp)))))
(append (letrec-build-sets (letrec-vars (letrec-bindings exp))
(letrec-vals (letrec-bindings exp)))
(letrec-body exp))))
(letrec-to-let example-letrec)
;; =>
;; (let ((even? *unassigned*) (odd? *unassigned*))
;; (set! even? (lambda (n) (if (= n 0) true (odd? (- n 1)))))
;; (set! odd? (lambda (n) (if (= n 0) false (even? (- n 1)))))
;; (message "ciao")
;; (message "hola"))b:
I had a bit of trouble doing part b of the exercise. But, after
looking on the web for what people have said and asking for help…,
the following should be the correct drawings. The key thing to notice,
assuming this is correct, is that, when using let (which is just a
lambda; see p. 64), the expressions whose evaluation gives the values
of the let bindings are not evaluated in the context of the new
frame created by the let, but they are evaluated in the context of
the frame to which the new frame created by the let points to (that
is, its “enclosing environment”). In a sense, we can say, they are
evaluated while the new frame is in the process of being created.
When using letrec, <rest of body of f> is evaluated in the following E2 frame:
E0
+-------------------+
|f:--+ |
| | |
| | |
+----+--------------+
| ^ ^
| | |
V | | E1
+---+---+ | | +--+------+---------+
| | | -+--+ +---+x: 5 |
+-+-+---+ +-------------------+
| ^
V |
... |
| E2
+-------+------------+
| even?:-------------+---------------+
| | |
| |<----------- |
| odd?:---+ | \ |
+---------+----------+ \ V
| ^ +---+-\-+
| | | | | +
| | +-+-+---+
V | |
+---+---+ | |
| | | -+--+ V
+-+-+---+ ...
|
|
V
...
When using let, <rest of body of f> is evaluated in the following E2 frame:
E0
+-------------------+
|f:--+ |
| | |
| | |
+----+--------------+
| ^ ^
| | |
V | | E1
+---+---+ | | +--+------+---------+ <----------------------------+
| | | -+--+ +---+x: 5 | <---------------------+ |
+-+-+---+ +-------------------+ | |
| ^ | |
V | | |
... | | |
| E2 | |
+-------+------------+ | |
| even?:-------------+---------------+ | |
| | | | |
| | | | |
| odd?:---+ | | | |
+---------+----------+ V | |
| +---+---+ | |
| | | | -+----+ |
| +-+-+---+ |
V | |
+---+---+ | |
| | | +---------+ V |
+-+-+---+ | ... |
| | |
| | |
V | |
... | |
| |
+--------------------------+
Exercise:
Amazingly, Louis’s intuition in Exercise 4.20 is correct. It is indeed possible to specify recursive procedures without using
letrec(or evendefine), although the method for accomplishing this is much more subtle than Louis imagined. The following expression computes 10 factorial by applying a recursive factorial procedure[fn::This example illustrates a programming trick for formulating recursive procedures without usingdefine. The most general trick of this sort is the Y “operator”, which can be used to give a “pure λ-calculus” implementation of recursion. (See Stoy 1977 for details on the λ calculus, and Gabriel 1988 for an exposition of the Y operator in Scheme.)].((lambda (n) ((lambda (fact) (fact fact n)) (lambda (ft k) (if (= k 1) 1 (* k (ft ft (- k 1))))))) 10)a. Check (by evaluating the expression) that this really does compute factorials. Devise an analogous expression for computing Fibonacci numbers.
b. Consider the following procedure, which includes mutually recursive internal definitions:
(define (f x) (define (even? n) (if (= n 0) true (odd? (- n 1)))) (define (odd? n) (if (= n 0) false (even? (- n 1)))) (even? x))Fill in the missing expressions to complete an alternative definition of
f, which uses neither internal definitions norletrec:(define (f x) ((lambda (even? odd?) (even? even? odd? x)) (lambda (ev? od? n) (if (= n 0) true (od? <??> <??> <??>))) (lambda (ev? od? n) (if (= n 0) false (ev? <??> <??> <??>)))))
Answer:
a:
((lambda (n)
((lambda (fib)
(fib fib n))
(lambda (ft k)
(cond ((= k 0)
0)
((= k 1)
1)
(else (+ (ft ft (- k 1))
(ft ft (- k 2))))))))
12) ;; => 144b:
(define (f x)
((lambda (even? odd?)
(even? even? odd? x))
(lambda (ev? od? n)
(if (= n 0) true (od? ev? od? (- n 1))))
(lambda (ev? od? n)
(if (= n 0) false (ev? ev? od? (- n 1))))))- Our evaluator is inefficient in that it interleaves syntactic analysis and execution of expressions.
- If a program is executed many times, then its syntax is expensively and wastefully analyzed each of those times.
- Consider:
(define (factorial n) (if (= n 1) 1 (* (factorial (- n 1)) n)))
Each time
factorialis called the evaluator must determine that the body is anifstatement and act accordingly. Each time(* (factorial (- n 1)) n),(factorial (- n 1)), and(- n 1)are evaluated, the evaluator must determine that they are applications and act accordingly. - Authors present a way, used by Jonathan Rees in 1982 and indepedently invented by Marc Feeley in 1986, to perform syntactic analysis only once.
Evalis split into two parts.- “The procedure
analyzetakes only the expression. It performs the syntactic analysis and returns a new procedure, the execution procedure, that encapsulates the work to be done in executing the analyzed expression. The execution procedure takes an environment as its argument and completes the evaluation. This saves work becauseanalyzewill be called only once on an expression, while the execution procedure may be called many times.” (394)(define (eval exp env) ((analyze exp) env)) (define (analyze exp) (cond ((self-evaluating? exp) (analyze-self-evaluating exp)) ((quoted? exp) (analyze-quoted exp)) ((variable? exp) (analyze-variable exp)) ((assignment? exp) (analyze-assignment exp)) ((definition? exp) (analyze-definition exp)) ((if? exp) (analyze-if exp)) ((begin? exp) (analyze-sequence (begin-action exp))) ((cond? exp) (analyze (cond->if exp))) ((application? exp) (analyze-application exp)) (else (error "Unknown expression type -- ANALYZE" exp)))) (define (analyze-self-evaluating exp) (lambda (env) exp)) (define (analyze-quoted exp) (let ((qval (text-of-quotation exp))) (lambda (env) qval))) ;; Looking up a variable depends upon knowing the environment, so it ;; must be done at execution time (Sec. 5.5.6 will show, though, how ;; to perform an important part of the variable search as part of the ;; syntactic analysis). (define (analyze-variable exp) (lambda (env) (lookup-variable-value exp env))) ;; Assignments and definitions, too, can be performed only when the ;; env is known. However, the recursive analysis of `assignment-value` ;; and `definition-value` during syntactic analys is a ``major gain in ;; efficiency''. (define (analyze-assignment exp) (let ((var (assignment-variable exp)) (vproc (analyze (assignment-value exp)))) (lambda (env) (set-variable-value! var (vproc env) env) 'ok))) (define (analyze-definition exp) (let ((var (definition-variable exp)) (vproc (analyze (definition-value exp)))) (lambda (env) (define-variable! var (vproc env) env) 'ok))) ;; We now analyze predicates, consequents, and alternatives of if ;; statements at analysis time: (define (analyze-if exp) (let ((pproc (analyze (if-predicate exp))) (cproc (analyze (if-consequent exp))) (aproc (analyze (if-alternative exp)))) (lambda (env) (if (true? (pproc env)) (cproc env) (aproc env))))) ;; λ: (define (analyze-lambda exp) (let ((vars (lambda-parameters exp)) (bproc (analyze-sequence (lambda-body exp)))) (lambda (env) (make-procedure vars bproc env)))) ;; The analysis of sequences is ``more involved'': ... (define (analyze-sequence exps) (define (sequentially proc1 proc2) (lambda (env) (proc1 env) (proc2 env))) (define (loop first-proc rest-procs) (if (null? rest-procs) first-proc (loop (sequentially first-proc (car rest-procs)) (cdr rest-procs)))) (let ((procs (map analyze exps))) (if (null? procs) (error "Empty sequence -- ANALYZE")) (loop (car procs) (cdr procs)))) ;; Finally, to analyze an application... (define (analyze-application exp) (let ((fproc (analyze (operator exp))) (aprocs (map analyze (operands exp)))) (lambda (env) (execute-application (fproc env) (map (lambda (aproc) (aproc env)) aprocs))))) (define (execute-application proc args) (cond ((primitive-procedure? proc) (apply-primitive-procedure proc args)) ((compound-procedure? proc) ((procedure-body proc) (extend-environment (procedure-parameters proc) args (procedure-environment proc)))) (else (error "Unknown procedure type -- EXECUTE-APPLICATION" proc))))
Exercise:
Extend the evaluator in this section to support the special form
let. (See Exercise 4.6)
Answer:
(define (analyze exp)
(cond ((self-evaluating? exp)
(analyze-self-evaluating exp))
((quoted? exp) (analyze-quoted exp))
((variable? exp) (analyze-variable exp))
((assignment? exp) (analyze-assignment exp))
((definition? exp) (analyze-definition exp))
((if? exp) (analyze-if exp))
((lambda? exp) (analyze-lambda exp))
((begin? exp) (analyze-sequence (begin-actions exp)))
((cond? exp) (analyze (cond->if exp)))
((let? exp) (analyze (let-combination exp)))
((application? exp) (analyze-application exp))
(else
(error "Unknown expression type -- ANALYZE" exp))))
;; where `let-combination' is the procedure (shown in the answer to
;; Exercise 4.6) that transforms a let expression into (the
;; application of) a lambda expression.Exercise:
Alyssa P. Hacker doesn’t understand why analyze-sequence needs to be
so complicated. All the other analysis procedures are straightforward
transformations of the corresponding evaluation procedures (or eval
clauses) in section 4.1.1. She expected analyze-sequence to look
like this:
(define (analyze-sequence exps)
(define (execute-sequence procs env)
(cond ((null? (cdr procs)) ((car procs) env))
(else ((car procs) env)
(execute-sequence (cdr procs) env))))
(let ((procs (map analyze exps)))
(if (null? procs)
(error "Empty sequence -- ANALYZE"))
(lambda (env) (execute-sequence procs env))))Eva Lu Ator explains to Alyssa that the version in the text does more of the work of evaluating a sequence at analysis time. Alyssa’s sequence-execution procedure, rather than having the calls to the individual execution procedures built in, loops through the procedures in order to call them: In effect, although the individual expressions in the sequence have been analyzed, the sequence itself has not been.
Compare the two versions of analyze-sequence. For example, consider
the common case (typical of procedure bodies) where the sequence has
just one expression. What work will the execution procedure produced
by Alyssa’s program do? What about the execution procedure produced
by the program in the text above? How do the two versions compare for
a sequence with two expressions?
Answer:
Let’s consider a sequence with one expression, the sequence which
contains the self-evaluating expression 1: (1).
This is what happens when the program in the main text is applied to that sequence:
procsis assigned this value:((lambda (env) 1))
loopis called:(loop (lambda (env) 1) nil)
- final value:
(lambda (env) 1)
- If we apply this latter value (which is a
lambda) to an environment, then it evaluates to1.
This, instead, is what happens with Alyssa’s program:
procsare assigned the same value they are assigned by the program in the main text;- final value:
(lambda (env) (execute-sequence ((lambda (env) q)) env))
- if this latter value is applied to an environment, then it evaluates
to this call:
((lambda (env) 1) env)
which evaluates to 1.
Let’s now consider the sequence with the self-evaluting expression 1
and the self-evaluting expression 2: (1 2).
This is what happens when the program in the main text is applied to that sequence:
procsis set to this value:((lambda (env) 1) (lambda (env) 2))
- we perform this application:
(loop (lambda (env) 1) ((lambda (env) 2)))
- then we perform this application:
(loop (lambda (env) (lambda (env) 1) (lambda (env) 2)) nil)
- This is the final value:
(lambda (env) ((lambda (env) 1 env)) ((lambda (env) 2) env))
This is what happens with Alyssa’s program:
procsis set to the same value as above;- Final value:
(lambda (env) (execute-sequence ((lambda (env) 1) (lambda (env) 2)) env))
- When we apply this final value (which is a
lambda) to an environment, we evaluate this application, which evaluates to 1:((lambda (env) 1) env)
But also also this one:
(execute-sequence ((lambda (env) 2)) env)
which evaluates to
((lambda (env) 2 ) env)
which evaluates to 2.
The program in the main text and Alyssa’s program give the same result. However, Alyssa’s program returns a lambda which does more work when it is called; it has to construct the final lambda calls. The program in the main text returns a lambda whose body already contains those final lambda calls.
- In applicative order languages like Scheme, the arguments to a procedures are all evaluated when the procedure is applied.
- In normal order languages, instead, the evaluation is peformed when the values are needed.
- Lazy evaluation consists in postponing the evaluation until the last possible moment.
- Consider the following procedure:
(define (try a b) (if (= a 0) 1 b))
Scheme would give an error if we try to evaluate
(try 0 (1 / 0)). It wouldn’t, though, if its evaluation were lazy. - Also consider:
(define (unless condition usual-value exceptional-value) (if condition exceptional-value usual-value))
This
(unless (= b 0) (/ a b) (begin (display "exception: returning 0") 0))
would not work in an applicative order language… But lazy evaluation has the benefit of letting procedures of this kind do useful computations.
- “If the body of a procedure is entered before an argument has been evaluated we say that the procedure is non-strict in that argument. If the argument is evaluated before the body of the procedure is entered we say that the procedure is strict in that argument.”
- (“The `strict’ versus `non-strict’ terminology means essentially the same thing as `applicative-order’ versus `normal-order’, except that it refers to individual procedures and arguments rather than to the language as a whole.”)
- “A striking example of a procedure that can usefully be made
non-strict is
cons(or, in general, almost any constructor for data structures).”
Exercise:
Suppose that (in ordinary applicative-order Scheme) we define unless
as shown above and then define factorial in terms of unless as
(define (factorial n)
(unless (= n 1)
(* n (factorial (- n 1)))
1))What happens if we attempt to evaluate (factorial 5)? Will our
definitions work in a normal-order language?
Answer:
In scheme (which is applicative order) we
At some point, the chain of recursive calls ends up calling unless
where n is bound to 1.
This means that the second argument passed to unless, if evaluated,
would entail the application of factorial to 0.
An applicative order evaluation language would evaluate it; so it would initiate an infinite chain of applications (because the terminating condition will never be satisfied).
But there should be no problem in a normal-order language.
Exercise:
Ben Bitdiddle and Alyssa P. Hacker disagree over the importance of lazy evaluation for implementing things such as
unless. Ben points out that it’s possible to implementunlessin applicative order as a special form. Alyssa counters that, if one did that,unlesswould be merely syntax, not a procedure that could be used in conjunction with higher-order procedures. Fill in the details on both sides of the argument. Show how to implementunlessas a derived expression (likecondorlet), and give an example of a situation where it might be useful to haveunlessavailable as a procedure, rather than as a special form.
Answer:
Remember Authors saying:
Some special forms in our language can be defined in terms of expressions involving other special forms, rather than being implemented directly (p. ?) […] Expressions (such as cond) that we choose to implement as syntactic transformations are called derived expressions.
That is the way Authors intend unless as a special form (i.e.,
defined in terms of if).
This is the way we can transform an unless expression into a if
expression:
(define (tagged-list? exp tag)
(if (pair? exp)
(eq? (car exp) tag)
false))
(define (unless? exp)
(tagged-list? exp 'unless))
(define (unless-condition exp)
(cadr exp))
(define (unless-usual-value exp)
(caddr exp))
(define (unless-exceptional-value exp)
(cadddr exp))
(define (unless->if exp)
(list 'if
(unless-condition exp)
(unless-exceptional-value exp)
(unless-usual-value exp)))So… by exploring a little bit, I found out that Authors say this in 4.2.3:
we showed how to implement streams as delayed lists. We introduced special forms delay and cons-stream… For one thing, a special form is not a first-class object like a procedure, so we cannot use it together with higher-order procedures.
This is basically the same thing that Alyssa is saying with respect to
unless when it is implemented as a special form in tersm of if. In
fact, Authors added a footnote that refer to our exercise. They don’t
seem to give any example, though.
Okay, let’s make some tests… if is a special, so let’s try to pass
it to a higher-order function.
(define BOH
(lambda (cond-eval-strategy cond alt1 alt2)
(cond-eval-strategy cond alt1 alt2)))
(BOH if #t 1 2) ;; => if: bad syntax in: ifWe get an error, indeed: if: bad syntax in: if.
How so? Let’s try with a normal procedure.
(define (gp/if cond alt1 alt2)
(if cond alt1 alt2))
(BOH gp/if #t 1 2) ;; => 1No error.
So… Ben is right that we can implement unless as a special
form. Alyssa is right in maintaining that, if implemented that way, it
could not be passed to higher-order procedures. The reason is that the
arguments of a procedures are evaluated; the evaluation of a lambda
expression yields a procedure object; but the evaluation of a special
form? It doesn’t really make sense, does it? (At least in our case.)
It’s kind of hard to think of a case where it would be useful to have
unless as a procedure. The only thing I can think of is something
like BOH, that is, a procedure that gives the user the choice of how
to deal with a certain condition.
Basic idea:
when applying a procedure, the interpreter must determine which arguments are to be evaluated and which are to be delayed.
The arguments to delay are turned into “thunks”. A thunk includes all the information we need to evaluate the argument and produce the same value which would have been produced normally at application time. When we squeeze a value out of a thunk we say that the thunk is “forced” — that information must include the relevant environment.
When do we need to force a thunk? Usually when:
- it is passed to a primitive procedure;
- it represents the predicate of a conditional;
- it represents the operator in an application.
Our interpreter will memoize the thunks.
We change the `application’ clause of eval:
((application? exp)
(apply (actual-value (operator exp) env)
(operands exp)
env))The operator is completely evaluated. The operands are left the way they are. We also need to pass the environment for apply to construct the thunk.
actual-value completely evaluates an expression:
(define (actual-value exp env)
(force-it (eval exp env)))apply now has to deal with unevaluated operand expressions. When it
deals with a primitve procedure, it evaluates all the arguments before
applying the primitive. When it deals with a compound procedure, it
delays all the arguments before applying the procedure.
(define (apply procedure arguments env)
(cond ((primitive-procedure? procedure)
(apply-primitive-procedure
procedure
(list-of-arg-values arguments env))) ; changed
((compound-procedure? procedure)
(eval-sequence
(procedure-body procedure)
(extend-environment
(procedure-parameters procedure)
(list-of-delayed-args arguments env) ; changed
(procedure-environment procedure))))
(else
(error
"Unknown procedure type -- APPLY" procedure))))
(define (list-of-arg-values exps env)
(if (no-operands? exps)
'()
(cons (actual-value (first-operand exps) env)
(list-of-arg-values (rest-operands exps)
env))))
(define (list-of-delayed-args exps env)
(if (no-operands? exps)
'()
(cons (delay-it (first-operand exps) env)
(list-of-delayed-args (rest-operands exps)
env))))eval-if also has to change:
(define (eval-if exp env)
(if (true? (actual-value (if-predicate exp) env))
(eval (if-consequent exp) env)
(eval (if-alternative exp) env)))Finally, we are also changing the driver-loop, because if some thunk has to be printed, then we want to force it:
(define input-prompt ";;; L-Eval input:")
(define output-prompt ";;; L-Eval value:")
(define (driver-loop)
(prompt-for-input input-prompt)
(let ((input (read)))
(let ((output
(actual-value input the-global-environment)))
(announce-output output-prompt)
(user-print output)))
(driver-loop))How are thunks implemented?
(define (force-it obj)
(cond ((thunk? obj)
(let ((result (actual-value
(thunk-exp obj)
(thunk-env obj))))
(set-car! obj 'evaluated-thunk)
(set-car! (cdr obj) result) ; replace `exp' with its value
(set-cdr! (cdr obj) '()) ; forget unneeded `env'
result))
((evaluated-thunk? obj)
(thunk-value obj))
(else obj)))
(define (delay-it exp env)
(list 'thunk exp env))
(define (thunk? obj)
(tagged-list? obj 'thunk))
(define (thunk-exp thunk) (cadr thunk))
(define (thunk-env thunk) (caddr thunk))
(define (evaluated-thunk? obj)
(tagged-list? obj 'evaluated-thunk))
(define (thunk-value evaluated-thunk) (cadr evaluated-thunk))Here is the modified evaluator.
#lang sicp
(define apply-in-underlying-scheme apply)
(define (evaluated-thunk? obj)
(tagged-list? obj 'evaluated-thunk))
(define (thunk-value evaluated-thunk) (cadr evaluated-thunk))
(define (force-it obj)
(cond ((thunk? obj)
(let ((result (actual-value
(thunk-exp obj)
(thunk-env obj))))
(set-car! obj 'evaluated-thunk)
(set-car! (cdr obj) result) ; replace `exp' with its value
(set-cdr! (cdr obj) '()) ; forget unneeded `env'
result))
((evaluated-thunk? obj)
(thunk-value obj))
(else obj)))
(define (delay-it exp env)
(list 'thunk exp env))
(define (thunk? obj)
(tagged-list? obj 'thunk))
(define (thunk-exp thunk) (cadr thunk))
(define (thunk-env thunk) (caddr thunk))
(define (actual-value exp env)
(force-it (eval exp env)))
(define (list-of-arg-values exps env)
(if (no-operands? exps)
'()
(cons (actual-value (first-operand exps) env)
(list-of-arg-values (rest-operands exps)
env))))
(define (list-of-delayed-args exps env)
(if (no-operands? exps)
'()
(cons (delay-it (first-operand exps) env)
(list-of-delayed-args (rest-operands exps)
env))))
(define (eval exp env)
(cond ((self-evaluating? exp) exp)
((variable? exp) (lookup-variable-value exp env))
((quoted? exp) (text-of-quotation exp))
((assignment? exp) (eval-assignment exp env))
((definition? exp) (eval-definition exp env))
((if? exp) (eval-if exp env))
((lambda? exp)
(make-procedure (lambda-parameters exp)
(lambda-body exp)
env))
((begin? exp)
(eval-sequence (begin-actions exp) env))
((cond? exp) (eval (cond->if exp) env))
((application? exp)
(apply-evaluator (actual-value (operator exp) env)
(operands exp)
env))
(else
(error "Unknown expression type -- EVAL" exp))))
(define (apply-evaluator procedure arguments env)
(cond ((primitive-procedure? procedure)
(apply-primitive-procedure
procedure
(list-of-arg-values arguments env))) ; changed
((compound-procedure? procedure)
(eval-sequence
(procedure-body procedure)
(extend-environment
(procedure-parameters procedure)
(list-of-delayed-args arguments env) ; changed
(procedure-environment procedure))))
(else
(error
"Unknown procedure type -- APPLY" procedure))))
(define (list-of-values exps env)
(if (no-operands? exps)
'()
(cons (eval (first-operand exps) env)
(list-of-values (rest-operands exps) env))))
(define (eval-if exp env)
(if (true? (actual-value (if-predicate exp) env))
(eval (if-consequent exp) env)
(eval (if-alternative exp) env)))
(define (eval-sequence exps env)
(cond ((last-exp? exps) (eval (first-exp exps) env))
(else (eval (first-exp exps) env)
(eval-sequence (rest-exps exps) env))))
(define (eval-assignment exp env)
(set-variable-value! (assignment-variable exp)
(eval (assignment-value exp) env)
env)
'ok)
(define (eval-definition exp env)
(define-variable! (definition-variable exp)
(eval (definition-value exp) env)
env)
'ok)
(define (self-evaluating? exp)
(cond ((number? exp) true)
((string? exp) true)
(else false)))
(define (variable? exp) (symbol? exp))
(define (quoted? exp)
(tagged-list? exp 'quote))
(define (text-of-quotation exp) (cadr exp))
(define (tagged-list? exp tag)
(if (pair? exp)
(eq? (car exp) tag)
false))
(define (assignment? exp)
(tagged-list? exp 'set!))
(define (assignment-variable exp) (cadr exp))
(define (assignment-value exp) (caddr exp))
(define (definition? exp)
(tagged-list? exp 'define))
(define (definition-variable exp)
(if (symbol? (cadr exp))
(cadr exp)
(caadr exp)))
(define (definition-value exp)
(if (symbol? (cadr exp))
(caddr exp)
(make-lambda (cdadr exp) ; formal parameters
(cddr exp)))) ; body
(define (lambda? exp) (tagged-list? exp 'lambda))
(define (lambda-parameters exp) (cadr exp))
(define (lambda-body exp) (cddr exp))
(define (make-lambda parameters body)
(cons 'lambda (cons parameters body)))
(define (if? exp) (tagged-list? exp 'if))
(define (if-predicate exp) (cadr exp))
(define (if-consequent exp) (caddr exp))
(define (if-alternative exp)
(if (not (null? (cdddr exp)))
(cadddr exp)
'false))
(define (make-if predicate consequent alternative)
(list 'if predicate consequent alternative))
(define (begin? exp) (tagged-list? exp 'begin))
(define (begin-actions exp) (cdr exp))
(define (last-exp? seq) (null? (cdr seq)))
(define (first-exp seq) (car seq))
(define (rest-exps seq) (cdr seq))
(define (sequence->exp seq)
(cond ((null? seq) seq)
((last-exp? seq) (first-exp seq))
(else (make-begin seq))))
(define (make-begin seq) (cons 'begin seq))
(define (application? exp) (pair? exp))
(define (operator exp) (car exp))
(define (operands exp) (cdr exp))
(define (no-operands? ops) (null? ops))
(define (first-operand ops) (car ops))
(define (rest-operands ops) (cdr ops))
(define (cond? exp) (tagged-list? exp 'cond))
(define (cond-clauses exp) (cdr exp))
(define (cond-else-clause? clause)
(eq? (cond-predicate clause) 'else))
(define (cond-predicate clause) (car clause))
(define (cond-actions clause) (cdr clause))
(define (cond->if exp)
(expand-clauses (cond-clauses exp)))
(define (expand-clauses clauses)
(if (null? clauses)
'false ; no `else' clause
(let ((first (car clauses))
(rest (cdr clauses)))
(if (cond-else-clause? first)
(if (null? rest)
(sequence->exp (cond-actions first))
(error "ELSE clause isn't last -- COND->IF"
clauses))
(make-if (cond-predicate first)
(sequence->exp (cond-actions first))
(expand-clauses rest))))))
(define (true? x)
(not (eq? x false)))
(define (false? x)
(eq? x false))
(define (make-procedure parameters body env)
(list 'procedure parameters body env))
(define (compound-procedure? p)
(tagged-list? p 'procedure))
(define (procedure-parameters p) (cadr p))
(define (procedure-body p) (caddr p))
(define (procedure-environment p) (cadddr p))
(define (enclosing-environment env) (cdr env))
(define (first-frame env) (car env))
(define the-empty-environment '())
(define (make-frame variables values)
(cons variables values))
(define (frame-variables frame) (car frame))
(define (frame-values frame) (cdr frame))
(define (add-binding-to-frame! var val frame)
(set-car! frame (cons var (car frame)))
(set-cdr! frame (cons val (cdr frame))))
(define (extend-environment vars vals base-env)
(if (= (length vars) (length vals))
(cons (make-frame vars vals) base-env)
(if (< (length vars) (length vals))
(error "Too many arguments supplied" vars vals)
(error "Too few arguments supplied" vars vals))))
(define (lookup-variable-value var env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (car vars))
(car vals))
(else (scan (cdr vars) (cdr vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))
(define (set-variable-value! var val env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (car vars))
(set-car! vals val))
(else (scan (cdr vars) (cdr vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable -- SET!" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))
(define (define-variable! var val env)
(let ((frame (first-frame env)))
(define (scan vars vals)
(cond ((null? vars)
(add-binding-to-frame! var val frame))
((eq? var (car vars))
(set-car! vals val))
(else (scan (cdr vars) (cdr vals)))))
(scan (frame-variables frame)
(frame-values frame))))
(define primitive-procedures
(list (list 'car car)
(list 'cdr cdr)
(list 'cons cons)
(list 'null? null?)
(list '= =)
(list '+ +)
(list '- -)
(list '* *)
(list '/ /)))
(define (primitive-procedure-names)
(map car
primitive-procedures))
(define (primitive-procedure-objects)
(map (lambda (proc) (list 'primitive (cadr proc)))
primitive-procedures))
(define (setup-environment)
(let ((initial-env
(extend-environment (primitive-procedure-names)
(primitive-procedure-objects)
the-empty-environment)))
(define-variable! 'true true initial-env)
(define-variable! 'false false initial-env)
initial-env))
(define (primitive-procedure? proc)
(tagged-list? proc 'primitive))
(define (primitive-implementation proc) (cadr proc))
(define (apply-primitive-procedure proc args)
(apply-in-underlying-scheme
(primitive-implementation proc) args))
(define input-prompt ";;; L-Eval input:")
(define output-prompt ";;; L-Eval value:")
(define (driver-loop)
(prompt-for-input input-prompt)
(let ((input (read)))
(let ((output
(actual-value input the-global-environment)))
(announce-output output-prompt)
(user-print output)))
(driver-loop))
(define (prompt-for-input string)
(newline) (newline) (display string) (newline))
(define (announce-output string)
(newline) (display string) (newline))
(define (user-print object)
(if (compound-procedure? object)
(display (list 'compound-procedure
(procedure-parameters object)
(procedure-body object)
'<procedure-env>))
(display object)))
(define the-global-environment (setup-environment))
(driver-loop)Try now to evaluate this:
(define (try a b)
(if (= a 0)
1
b))
(try 0 (/ 1 0))Exercise:
Suppose we type in the following definitions to the lazy evaluator:
(define count 0)
(define (id x)
(set! count (+ count 1))
x)Give the missing values in the following sequence of interactions, and explain your answers.(5)
(define w (id (id 10)))
;;; L-Eval input:
count
;;; L-Eval value:
<RESPONSE>
;;; L-Eval input:
w
;;; L-Eval value:
<RESPONSE>
;;; L-Eval input:
count
;;; L-Eval value:
<RESPONSE>Answer:
The first <RESPONSE> is 1 (I thought it was 0…). When we evaluate
(define w (id (id 10))), among other things, we apply eval to the
“definition-value”, that is, to (id (id 10)).
That’s the application of a compound procedure (of the outer
id). Regardless of lazy evaluation, that means we are going to
evaluate the expressions of the body of id (in an environment in
which the parameters are set to delayed values).
This means, first, that the set! in the body is evaluated, so
count won’t be 1 anymore. And, second, that the value of the final
expression — that value w is set to — will be a thunk.
The second <RESPONSE> is 10: we are trying to print a thunk, so the thunk is forced (remember the modification we made to the driver loop).
The third <RESPONSE> is 2. To print the value of w we nee to perform
the application of the inner id (which entails increasing count
for the second time).
Exercise:
Evalusesactual-valuerather thanevalto evaluate the operator before passing it toapply, in order to force the value of the operator. Give an example that demonstrates the need for this forcing.
Example: higher order functions. E.g., map.
;; Unmodified evaluator (using `actual-value'):
;;; L-Eval input:
(define (add1 x)
(+ x 1))
;;; L-Eval value:
ok
;;; L-Eval input:
(define (map proc items)
(if (null? items)
'()
(cons (proc (car items))
(map proc (cdr items)))))
;;; L-Eval value:
ok
;;; L-Eval input:
(map add1 '(1 2 3))
;;; L-Eval value:
(2 3 4);; Using `eval' instead of `actual-value':
;;; L-Eval input:
(define (add1 x)
(+ x 1))
;;; L-Eval value:
ok
;;; L-Eval input:
(add1 5)
;;; L-Eval value:
6
;;; L-Eval input:
(define (map proc items)
(if (null? items)
'()
(cons (proc (car items))
(map proc (cdr items)))))
;;; L-Eval value:
ok
;;; L-Eval input:
(map add1 '(1 2 3))
. . Unknown procedure type -- APPLY (thunk add1 #0=(((map add1 try false true car cdr cons null? = + - * /) (procedure (proc items) ((if (null? items) '() (cons (proc (car items)) (map proc (cdr items))))) #0#) (procedure (x) ((+ x 1)) #0#) (procedure (a b) ((if (= a 0) 1 b)) #0#) #...Exercise:
Exhibit a program that you would expect to run much more slowly
without memoization than with memoization. Also, consider the
following interaction, where the id procedure is defined as in *Note 4.27
and count starts at 0:
(define (square x)
(* x x))
;;; L-Eval input:
(square (id 10))
;;; L-Eval value:
<RESPONSE>
;;; L-Eval input:
count
;;; L-Eval value:
<RESPONSE>Give the responses both when the evaluator memoizes and when it does not.
Answer:
The argument of (square (id 10)) is delayed (turned into a thunk),
In the body of square, though, we have the application of a
primitive procedure ((* thunk thunk)) so the thunks must be
forced. Given that the two thunks are the same thunk, if se memoize,
then the final <RESPONSES> is 1, otherwise is 2. The first <RESPONSES>
is 100, regardless of whether we memoize or not.
Clearly memoization will entail an improvement in performance in those cases in which we need the value for the same thunk many times and where forcing the thunk requires non-trivial computation.
The procedures fact and fib are two example where a difference can
be seen.
(eval '(define (fact n)
(if (= n 1)
1
(* n (fact (- n 1)))))
the-global-environment)
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1))
(fib (- n 2))))))Let’s test fact:
(define start (runtime))
(eval '(define (fact n)
(if (= n 1)
1
(* n (fact (- n 1)))))
the-global-environment)
(eval '(fact 140)
the-global-environment)
(display (- (runtime) start))With memoization:
;; ok
;; 13462012475717524605876073858941615558355851148193967190051391468057460367090535696797920946629681836680869097041958983702264048370902871114013579941370766400374327741701139895604871545254810788060989321379840000000000000000000000000000000000
;; 1556Without memoization:
;; ok
;; 13462012475717524605876073858941615558355851148193967190051391468057460367090535696797920946629681836680869097041958983702264048370902871114013579941370766400374327741701139895604871545254810788060989321379840000000000000000000000000000000000
;; 53581When calling (fact <EXP>), <EXP> is turned into a thunk. So the
body of fact will be evaluated in an environment where n (the
parameter name tow hich <EXP> corresponds to) is bound to that
thunk. Given the body of fact we need the value of n twice (when
n is not 1). Getting the value of n requires looking up the value
of the variable in the environment. If we memoize, then we need to do
that once (the second time we already have the value in the thunk we
has become an evaluated-thunk). If we don’t memoize, then we need to
do it twice. Mutatis mutandis for fib.
Cy D. Fect, a reformed C programmer, is worried that some side effects may never take place, because the lazy evaluator doesn’t force the expressions in a sequence. Since the value of an expression in a sequence other than the last one is not used (the expression is there only for its effect, such as assigning to a variable or printing), there can be no subsequent use of this value (e.g., as an argument to a primitive procedure) that will cause it to be forced. Cy thus thinks that when evaluating sequences, we must force all expressions in the sequence except the final one. He proposes to modify
eval-sequencefrom section 4-1-1 to useactual-valuerather thaneval:(define (eval-sequence exps env) (cond ((last-exp? exps) (eval (first-exp exps) env)) (else (actual-value (first-exp exps) env) (eval-sequence (rest-exps exps) env))))a. Ben Bitdiddle thinks Cy is wrong. He shows Cy the
for-eachprocedure described in Exercise 2-23, which gives an important example of a sequence with side effects:(define (for-each proc items) (if (null? items) 'done (begin (proc (car items)) (for-each proc (cdr items)))))He claims that the evaluator in the text (with the original
eval-sequence) handles this correctly:;;; L-Eval input: (for-each (lambda (x) (newline) (display x)) (list 57 321 88)) 57 321 88 ;;; L-Eval value: doneExplain why Ben is right about the behavior of
for-each.b. Cy agrees that Ben is right about the
for-eachexample, but says that that’s not the kind of program he was thinking about when he proposed his change toeval-sequence. He defines the following two procedures in the lazy evaluator:(define (p1 x) (set! x (cons x '(2))) x) (define (p2 x) (define (p e) e x) (p (set! x (cons x '(2)))))What are the values of
(p1 1)and(p2 1)with the originaleval-sequence? What would the values be with Cy’s proposed change toeval-sequence?c. Cy also points out that changing
eval-sequenceas he proposes does not affect the behavior of the example in part a. Explain why this is true.d. How do you think sequences ought to be treated in the lazy evaluator? Do you like Cy’s approach, the approach in the text, or some other approach?
Answer:
a.
There is nothing to force in the example. For the expressions in the sequences are not thunks.
When we evaluate
(begin
(display "foo")
...)We are going, among other things, to apply eval to (display
"foo"). And that is enough to carry out the complete application of
display to "foo".
b.
When using the original eval-sequence, the value of (p1 1) is (1
2): the evaluation of p1’s definition creates a procedure object
whose environment is the global environment. The application of p1
to 1, first, creates a a new environment by extending the global
environment with a frame which binds x to a thunk whose expression
is 1 and whose environment is the global evironment; and, second,
evaluates the body of of p1 within that environment. This latter
evaluation entails the application of eval to (set! x (cons x
'(2))) and x. The evaluation of (set! x (cons x '(2))) entails
the forcing of x, because primitive procedures must receive values
they can understand — not thunks. So the value of x is set to (1
2).
When using Cy’s eval-sequence, the value of (p1 1) should be (1
2) as well.
When using the original eval-sequence, the value of (p2 1) is a
thunk:
The evaluation of p2’s definition creates a procedure object whose
environment is the global environment.
The application of p2 to 1, first, creates a new environment by
extending the global environment with a frame which binds x to a
thunk whose expression is 1 and whose environment is the global
evironment; and, second, evaluates the body of of p2 within that
environment. This latter evaluation entails the evaluation of the
definition of p and the application of p to (set! x (cons x
'(2))).
The evaluation of the definition of p creates a procedures object
whose environment is the environment p2 points to.
The application of p to (set! x (cons x '(2))), first, creates a
new environment by extending the environment p points to with a
frame which binds e to a thunk whose expression is (set! x (cons x
'(2))) and whose environemnt is the environment p points to.
This latter evaluation entails the evaluation of e and x (in the
environemnt p points to). e evaluates to the thunk described above
and nothing is done with it. x evaluates to the other thunk
described above and it is returned (it is the value of the p’s
application). So the final value is that thunk.
When using Cy’s eval-sequence, the value of (p2 1) should be (1
2) — that’s because we are not applying eval to e; we are
applying actual-value to it.
c.
The difference between the old eval-sequence and the new one wit
respect to the example in a. is that, when using the old procedure, we
apply eval to (proc (car items)), whereas, when using the new one,
we apply actual-value~ to it.
When we apply eval to (proc (car items)), items have already
been forced, because null? has been applied to them. proc is
forced, because it is the operator of an application. So the value of
the application of eval is the expression’s actual value.
When we apply actual-value to (proc (car items)), there is an
extra step: we passed the evaluated value to force-it. But since the
value is not a thunk, nothing changes.
d.
Cy’s seems a better approach, since i) it ensures that side effects take place in both a-type cases and b-type cases, and ii) the difference with the other approach is minimal when it comes to a-type cases.
The approach taken in this section is somewhat unpleasant, because it makes an incompatible change to Scheme. It might be nicer to implement lazy evaluation as an upward-compatible extension, that is, so that ordinary Scheme programs will work as before. We can do this by extending the syntax of procedure declarations to let the user control whether or not arguments are to be delayed. While we’re at it, we may as well also give the user the choice between delaying with and without memoization. For example, the definition
(define (f a (b lazy) c (d lazy-memo)) ...)would define
fto be a procedure of four arguments, where the first and third arguments are evaluated when the procedure is called, the second argument is delayed, and the fourth argument is both delayed and memoized. Thus, ordinary procedure definitions will produce the same behavior as ordinary Scheme, while adding the `lazy-memo’ declaration to each parameter of every compound procedure will produce the behavior of the lazy evaluator defined in this section. Design and implement the changes required to produce such an extension to Scheme. You will have to implement new syntax procedures to handle the new syntax for `define’. You must also arrange for `eval’ or `apply’ to determine when arguments are to be delayed, and to force or delay arguments accordingly, and you must arrange for forcing to memoize or not, as appropriate.
Answer:
- Changes:
apply-evaluator, instead of usinglist-of-delayed-args, useslist-of-argswhich can decide whether to delay an argument or not, since it receives that information that, thanks to the new syntax, is possibly included in the parameters (I’m packing that information into the arguments thatlist-of-argsreceives).- When we delay an argument, we create a thunk which now contains
information about whether the forcing should use memoization or
not. More concretely, the second element of the thunk is now
either the symbol
memoor the symbolno-memo.
- Here are new and modified methods:
(define (to-delay? arg-with-info) (cond ((not (pair? arg-with-info)) (error "arg-with-info is expected to be a pair")) (else (or (eq? (car arg-with-info) 'lazy) (eq? (car arg-with-info) 'lazy-memo))))) (define (arg arg-with-info) (cdr arg-with-info)) ;; apply either `actual-value` or `delay-it` depending on the symbol ;; attached (define (list-of-args exps env) (if (no-operands? exps) '() (cons (actual-value-or-delay (first-operand exps) env) (list-of-args (rest-operands exps) env)))) (define (actual-value-or-delay operand-with-info env) (if (to-delay? operand-with-info) (delay-it operand-with-info env) (actual-value (arg operand-with-info) env))) (define (make-args-with-info args params-with-info) (if (null? args) '() (if (pair? (car params-with-info)) (cons (cons (memo-info-symbol (car params-with-info)) (car args)) (make-args-with-info (cdr args) (cdr params-with-info))) (cons (cons 'non-lazy (car args)) (make-args-with-info (cdr args) (cdr params-with-info)))))) (define (memo-info-symbol param-with-info) (cadr param-with-info)) (define (force-it obj) (cond ((thunk? obj) (if (eq? (cadr obj) 'lazy) ;; no memo (actual-value (thunk-exp obj) (thunk-env obj)) (let ((result (actual-value ;; memo (thunk-exp obj) (thunk-env obj)))) (set-car! obj 'evaluated-thunk) (set-car! (cdr obj) result) (set-cdr! (cdr obj) '()) result))) ((evaluated-thunk? obj) (thunk-value obj)) (else obj))) ;; it expects the exp to be tagged with either 'lazy or 'lazy-memo (define (delay-it exp env) (if (to-memo? exp) (list 'thunk 'memo (cdr exp) env) (list 'thunk 'no-memo (cdr exp) env))) (define (to-memo? exp) (eq? (car exp) 'lazy-memo)) (define (thunk-exp thunk) (caddr thunk)) (define (thunk-env thunk) (cadddr thunk)) (define (apply-evaluator procedure arguments env) (cond ((primitive-procedure? procedure) (apply-primitive-procedure procedure (list-of-arg-values arguments env))) ((compound-procedure? procedure) (eval-sequence (procedure-body procedure) (extend-environment (procedure-parameters-names procedure) (list-of-args (make-args-with-info arguments (procedure-parameters procedure)) env) (procedure-environment procedure)))) (else (error "Unknown procedure type -- APPLY" procedure)))) (define (procedure-parameters-names proc) (param-names (cadr proc))) (define (param-names params-with-info) (cond ((null? params-with-info) '()) ((pair? (car params-with-info)) (cons (car (car params-with-info)) (param-names (cdr params-with-info)))) (else (cons (car params-with-info) (param-names (cdr params-with-info))))))
Exercise:
Give some examples that illustrate the difference between the streams of chapter 3 and the “lazier” lazy lists described in this section. How can you take advantage of this extra laziness?
Answer:
First of all, here a way in which we can add the lazy lists feature to the evaluator:
;; remove cons, car and cdr from primitive procedures
(define primitive-procedures
(list (list 'null? null?)
(list '= =)
(list '+ +)
(list '- -)
(list '* *)
(list '/ /)
(list 'newline newline)
(list 'display display)))
;; add new cons, car and cdr to env, by modifying setup-environment
(define (setup-environment)
(let ((initial-env
(extend-environment (primitive-procedure-names)
(primitive-procedure-objects)
the-empty-environment)))
(define-variable! 'cons (make-procedure '(x y) '((lambda (m) (m x y))) initial-env) initial-env)
(define-variable! 'car (make-procedure '(z) '((z (lambda (p q) p))) initial-env) initial-env)
(define-variable! 'cdr (make-procedure '(z) '((z (lambda (p q) q))) initial-env) initial-env)
(define-variable! 'true true initial-env)
(define-variable! 'false false initial-env)
initial-env))Here are a couple of examples.
In normal scheme (racket), cons is strict in both arguments:
#lang sicp
(define (foo)
(display "foo!")
(newline)
"foo")
(cons (foo) (foo))
;; foo!
;; foo!
;; ("foo" . "foo")The cons of chapter 3 streams is strict in the first argument and
non-strict in the second:
(define (foo)
(display "foo!")
(newline)
"foo")
(cons-stream (foo) (foo))
;; foo!
;; ("foo" . #<promise>)The cons of chapter 4 lazy lists is non-strict on both arguments:
;;; L-Eval input:
(define (foo)
(display "foo!")
(newline)
"foo")
;;; L-Eval value:
ok
;;; L-Eval input:
(cons (foo) (foo))
;;; L-Eval value:
(compound-procedure (m) ((m x y)) <procedure-env>)Here is an example of the extra-lazyness Authors mention:
With chapter 3 streams, calling stream-cdr forces the cdr:
#lang sicp
(define (stream-car stream) (car stream))
(define (stream-cdr stream) (force (cdr stream)))
(define (foo)
(display "foo!")
(newline)
"foo")
(define foovar (cons-stream (foo) (foo)))
;; foo!
(define foovarcar (stream-car foovar))
(define foovarcdr (stream-cdr foovar))
;; foo!With chapter 4 lazy lists, neither the application of cdr nor of car
forces delayed value:
;;; L-Eval input:
(define (foo) (display "foo!") (newline) "foo")
;;; L-Eval value:
ok
;;; L-Eval input:
(define foovar (cons (foo) (foo)))
;;; L-Eval value:
ok
;;; L-Eval input:
(define foovarcar (car foovar))
;;; L-Eval value:
ok
;;; L-Eval input:
(define foovarcdr (cdr foovar))
;;; L-Eval value:
okChapter 3 streams are lazy at construction time with respect to the
cdr. They are non-lazy with respect to everything else.
Chapter 4 lazy lists are lazy both at construction time and at
selection time with respect to both the car and the cdr. Delayed
values are forced only when they are “really needed — e.g., for use
as the argument of a primitive, or to be printed as an answer.”
We can take advantage of the fact that the actual value of the car
is not computed at construction time. If the application of foo
involves a lot of computations, then (cons-stream (foo) nil) will
make them, wheres the lazy cons of chapter 3 won’t.
And we can take advantage of the fact that the selection of the cdr
does not entail its actual value in situation where its actual value
is not needed. For example, computing the length of a
stream/lazy-list:
Streams of chapter 3:
(define (stream-car stream) (car stream))
(define (stream-cdr stream) (force (cdr stream)))
(define (foo)
(display "foo!")
(newline)
"foo")
(define foolist
(cons-stream (foo)
(cons-stream (foo)
(cons-stream (foo) nil))))
(define (length stream-items)
(if (stream-null? stream-items)
0
(+ 1 (length (stream-cdr stream-items)))))
(length foolist)
;; foo!
;; foo!
;; foo!
;; 3Lazy lists of chapter 4:
;;; L-Eval input:
(define (length items) (if (null? items) 0 (+ 1 (length (cdr items)))))
;;; L-Eval value:
ok
;;; L-Eval input:
(define (foo) (display "foo!") (newline) "foo")
;;; L-Eval value:
ok
;;; L-Eval input:
(define foolist (cons (foo) (cons (foo) (cons (foo) '()))))
;;; L-Eval value:
ok
;;; L-Eval input:
(length foolist)
;;; L-Eval value:
3Exercise:
Ben Bitdiddle tests the lazy list implementation given above by evaluating the expression
(car '(a b c))To his surprise, this produces an error. After some thought, he realizes that the “lists” obtained by reading in quoted expressions are different from the lists manipulated by the new definitions of `cons’, `car’, and `cdr’. Modify the evaluator’s treatment of quoted expressions so that quoted lists typed at the driver loop will produce true lazy lists.
Answer:
(define (is-non-empty-list? exp)
(and (quoted? exp)
(list? (text-of-quotation exp))
(not (null? (text-of-quotation exp)))))
(define (list->cons exp)
(if (null? exp)
''()
(list
'cons
(car exp)
(list->cons (cdr exp)))))
(define (eval exp env)
(cond ((self-evaluating? exp) exp)
((variable? exp) (lookup-variable-value exp env))
((is-non-empty-list? exp) (eval (list->cons (cadr exp)) env));;<-------------
((quoted? exp) (text-of-quotation exp))
((assignment? exp) (eval-assignment exp env))
((definition? exp) (eval-definition exp env))
((if? exp) (eval-if exp env))
((lambda? exp)
(make-procedure (lambda-parameters exp)
(lambda-body exp)
env))
((begin? exp)
(eval-sequence (begin-actions exp) env))
((cond? exp) (eval (cond->if exp) env))
((application? exp)
(apply-evaluator (actual-value (operator exp) env)
(operands exp)
env))
(else
(error "Unknown expression type -- EVAL" exp))))