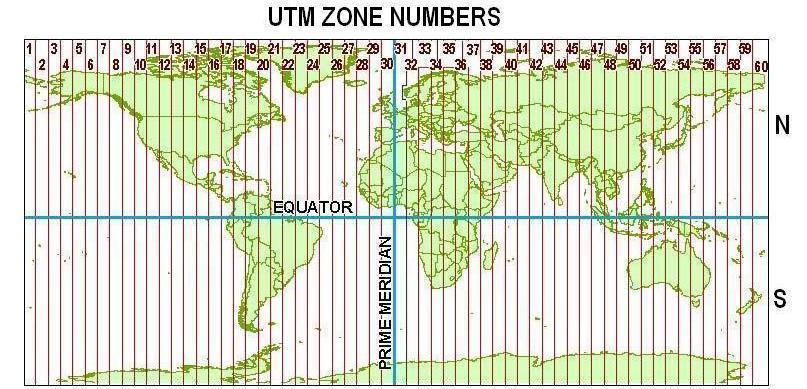
These functions enable the automated conversion between decimal and UTM coordinates in R. Previously, the conversion of coordinate systems was only possible in GIS software or through subscription-based third party entities.
This code was developed over the course of a brief undergraduate research assistantship with Professor Olivier Parent, a spatial econometrician at the University of Cincinnati.
The function enables coordinate conversion between the following coordinate systems:
- Decimal Degrees (LatLong)
- Universal Transverse Mercator (UTM)
This code is written as lightweight and computationally efficient. It prioritizes the need to convert large amounts of data. Moreover, the functions are structured intuitively. Inputs are segmented into idiosyncratic input parameters. This may require the user to conduct pre-emptive wrangling to shape the data into the correct format.
Each common conversion pair comes with a function. For instance, the _LLtoUTM.R file contains the function converting Decimal Degrees to UTM and the _UTMtoLL.R file converts in the opposite order.
Let us take a look at this function:
To avoid inaccuracy, misspecification, or errors, each function is designed to receive each component of the coordinate system separately.
# The shell of the LL to UTM function
LLtoUTM <- function (ellipsoid_name, lat, long) {
...
}
# The shell of the UTM to LL function
UTMtoLL <- function (ellipsoid_name, UTMNorthing, UTMEasting, UTMZone, UTMBand){
...
}
Note how both functions require different input parameters due to the structure of the respective input coordinate system. Aside from the coordinate-specific inputs, all functions require the specification of the ellipsoid. While almost all modern U.S.-based coordinate systems rely on the WGS_84 datum, this may vary for older data and for different regions. The WGS_84 datum can be thought of as the basis for the three-dimensional projection of any coordinate system.
The function body is mainly derived from the U.S. Geological Survey, such as Professional Paper 1395. In that sense, most of the code is derived from the equations set forth in these key pieces of literature.
As a next example, the mathematical mechanics of the conversion process are detailed. The following code is taken from the _LLtoUTM.R file.
################################################################################
### Define Ellipsoids and Their Parameters
################################################################################
# Aggregate equitorial and polar radii for 12 common ellipsoids ----------------
ellipsoid_df <- data.frame(
ellipsoid_name = c("Airy", "Australian", "Bessel_1841",
"Clarke_1866", "Clarke_1880", "Everest",
"Fischer_1960", "International_1924", "South_American_1969",
"WGS_72", "GRS_80", "WGS_84"),
a = c(6377563, 6378160, 6377397, #Semi-Major Axis "Equitorial Radius" [m]
6378206, 6378249, 6377276,
6378155, 6378388, 6378160,
6378135, 6378137, 6378137),
b = c(6356257, 6356775, 6356079, #Semi-Minor Axis "Polar Radius" [m]
6356584, 6356516, 6356075,
6356773, 6356912, 6356774,
6356751, 6356752, 6356752)
)
#Data retrieved from an NPS Distributed Learning Module (Coordinates and Maps)
#https://www.oc.nps.edu/oc2902w/c_mtutor/shape/shape5.htm
#Department of Oceanography, Naval Postgraduate School
#Contact: clynch@nps.navy.mil
#Accessed on: December 27th, 2022
# Calculate ellipsoidal parameters ---------------------------------------------
ellipsoid_df %<>%
mutate(f = (a - b) / a) %>% #Calculate flattening
mutate(inv_f = 1 / f) %>% #Calculate inverse flattening
mutate(ecc_sq = 2*f - f^2) #Calculate eccentricity squared
#Formulas retrieved from Peter H. Dana's website
#https://foote.geography.uconn.edu/gcraft/notes/coordsys/coordsys_f.html
#The Geographer’s Craft Project, Department of Geography, UConn
#Contact: pdana@pdana.com; ken.foote@uconn.edu
#Accessed on: December 27th, 2022
# Define additional ellipsoidal parameters -------------------------------------
k0 = 0.9996 #Central meridian scale factor
#Value retrieved from the U.S. Geological Survey
#(USGS) Professional Paper 1395 (1987) (p.57, ¶3)
#https://pubs.usgs.gov/pp/1395/report.pdf
#Accessed on: December 27th, 2022
################################################################################
### Function Body
################################################################################
# Retrieve ellipsoidal parameters by ellipsoid -------------------------------
#Retrieve equatorial radius by ellipsoid
a = ellipsoid_df$a[which(ellipsoid_df$ellipsoid_name
== ellipsoid_name)]
#Retrieve eccentricity squared by ellipsoid
ecc_sq = ellipsoid_df$ecc_sq[which(ellipsoid_df$ellipsoid_name
== ellipsoid_name)]
# Convert to Radians ---------------------------------------------------------
lat_rad <- lat*pi/180
long_rad <- long*pi/180
# Calculate Longitudinal Projection Zones ("Zones") --------------------------
UTMZone<- NULL #Empty vector shell
for(i in 1:length(long)){
#Definition of Svalbard zones
if(lat[i] >= 72.0 && lat[i] < 84.0){
#There are four irregular zones near Svalbard
if(long[i] >= 0.0 && long[i] < 9.0){ #Zone 31
UTMZone[i]<- "31"
} else if(long[i] >= 9.0 && long[i] < 21.0){ #Zone 33
UTMZone[i]<- "33"
} else if(long[i] >= 21.0 && long[i] < 33.0){ #Zone 35
UTMZone[i]<- "35"
} else if(long[i] >= 33.0 && long[i] < 42.0){ #Zone 37
UTMZone[i]<- "37"
}
}
#There is one irregular zone for Norway
else if(lat[i] >= 56.0 && lat[i] < 64.0 && #Define Norway Zone
long[i] >= 3.0 && long[i] < 12.0){
UTMZone[i]<- "32" #Zone 32
}
#Calculation of regular zones
else{
#Calculation/ standardization
UTMZone<- floor(((long + 180)/6) %% 60) + 1
}
}
#Convert results to numeric strings
UTMZone <- as.numeric(UTMZone)
#Data retrieved from the U.S. Geological Survey (USGS)
#Professional Paper 1395 (1987) (p.62, Figure 11)
#https://pubs.usgs.gov/pp/1395/report.pdf
#Accessed on: January 10th, 2023
# Define Formulas for Calculation --------------------------------------------
#Calculate the central meridian of a 6 degree wide UTM zone
long_origin = (UTMZone - 1)*6 - 180 + 3
long_origin_rad = long_origin*(pi/180)
#Variables
#USGS Professional Paper 1395 (1987), p.61 (8-12)
eccprime_sq = (ecc_sq^2)/(1 - ecc_sq^2)
#USGS Professional Paper 1395 (1987), p.61 (4-20)
N = a/sqrt(1-ecc_sq*sin(lat_rad)*sin(lat_rad))
#USGS Professional Paper 1395 (1987), p.61 (8-13)
T = tan(lat_rad)*tan(lat_rad)
#USGS Professional Paper 1395 (1987), p.61 (8-14)
C = eccprime_sq*cos(lat_rad)*cos(lat_rad)
#USGS Professional Paper 1395 (1987), p.61 (8-15)
A = cos(lat_rad)*(long_rad - long_origin_rad)
#Calculate the distance along central meridian from the Equator to lat_rad
#USGS Professional Paper 1395 (1987), p.61 (3-21)
M = a*((1
- ecc_sq/4
- 3*ecc_sq*ecc_sq/64
- 5*ecc_sq*ecc_sq*ecc_sq/256)*lat_rad
- (3*ecc_sq/8
+ 3*ecc_sq*ecc_sq/32
+ 45*ecc_sq*ecc_sq*ecc_sq/1024)*sin(2*lat_rad)
+ (15*ecc_sq*ecc_sq/256 + 45*ecc_sq*ecc_sq*ecc_sq/1024)*sin(4*lat_rad)
- (35*ecc_sq*ecc_sq*ecc_sq/3072)*sin(6*lat_rad))
#Formulas retrieved from the U.S. Geological Survey (USGS)
#Professional Paper 1395 (1987) (p.61)
#https://pubs.usgs.gov/pp/1395/report.pdf
#Accessed on: January 10th, 2023
# Calculate UTM Coordinates --------------------------------------------------
#Calculate Easting Coordinates
#USGS Professional Paper 1395 (1987), p.61 (8-9)
UTMEasting = (k0*N*(A+(1-T+C)*A*A*A/6
+ (5-18*T+T*T+72*C-58*eccprime_sq)*A*A*A*A*A/120)
+ 500000.0)
#Calculate Northing Coordinates
#USGS Professional Paper 1395 (1987), p.61 (8-10)
UTMNorthing = (k0*(M+N*tan(lat_rad)*
(A*A/2+(5-T+9*C+4*C*C)*A*A*A*A/24
+ (61-58*T+T*T+600*C
- 330*eccprime_sq)*A*A*A*A*A*A/720)))
#Adjust 1e7 meters if the coordinates are in the Southern hemisphere
if (lat[i] < 0) {
#USGS Professional Paper 1395 (1987), p.58, ¶2
UTMNorthing = UTMNorthing + 1e7
} else {
UTMNorthing = UTMNorthing
}
#Formulas retrieved from the U.S. Geological Survey (USGS)
#Professional Paper 1395 (1987) (p.61)
#https://pubs.usgs.gov/pp/1395/report.pdf
#Accessed on: January 10th, 2023
# Assign Latitudinal Letter Designator ---------------------------------------
UTMBand<-NULL #Empty vector shell
for(i in 1:length(lat)){
if(84 >= lat[i] && lat[i] >= 72){ #X band
UTMBand[i] <- "X"
} else if(72 > lat[i] && lat[i] >= 64){ #W band
UTMBand[i] <- "W"
} else if(64 > lat[i] && lat[i] >= 56){ #V band
UTMBand[i] <- "V"
} else if(56 > lat[i] && lat[i] >= 48){ #U band
UTMBand[i] <- "U"
} else if(48 > lat[i] && lat[i] >= 40){ #T band
UTMBand[i] <- "T"
} else if(40 > lat[i] && lat[i] >= 32){ #S band
UTMBand[i] <- "S"
} else if(32 > lat[i] && lat[i] >= 24){ #R band
UTMBand[i] <- "R"
} else if(24 > lat[i] && lat[i] >= 16){ #Q band
UTMBand[i] <- "Q"
} else if(16 > lat[i] && lat[i] >= 8){ #P band
UTMBand[i] <- "P"
} else if(8 > lat[i] && lat[i] >= 0){ #N band
UTMBand[i] <- "N"
} else if(0 > lat[i] && lat[i] >= -8){ #M band
UTMBand[i] <- "M"
} else if(-8 > lat[i] && lat[i] >= -16){ #L band
UTMBand[i] <- "L"
} else if(-16 > lat[i] && lat[i] >= -24){ #K band
UTMBand[i] <- "K"
} else if(-24 > lat[i] && lat[i] >= -32){ #J band
UTMBand[i] <- "J"
} else if(-32 > lat[i] && lat[i] >= -40){ #H band
UTMBand[i] <- "H"
} else if(-40 > lat[i] && lat[i] >= -48){ #G band
UTMBand[i] <- "G"
} else if(-48 > lat[i] && lat[i] >= -56){ #F band
UTMBand[i] <- "F"
} else if(-56 > lat[i] && lat[i] >= -64){ #E band
UTMBand[i] <- "E"
} else if(-64 > lat[i] && lat[i] >= -72){ #D band
UTMBand[i] <- "D"
} else if(-72 > lat[i] && lat[i] >= -80){ #C band
UTMBand[i] <- "C"
} else{
UTMBand[i] <- "Z" #Z band
}
}
Each function begins with defining a set of ellipsoids ("datum") used for the three-dimensional projection of the coordinate system. Depending on the choice of datum, a set of ellipsoidal parameters are calculated. Those can be thought of as the parameters thats et forth our closest approximation to the shape of the earth (The choice of different ellipsoids is motivated by people fundamentally disagreeing on this set of parameters).
The _LLtoUTM.R file then proceeds by
- Calculating the UTM Zone (while accounting for exceptions in the grid such as Svalbard)
- Obtaining the Northing and Easting coordinates through a sequence of geodetic formulas
- Assigning a UTM Band
For suggestions, comments, or concerns, please do not hesitate to reach out to me at posmikdc[at]gmail[dot]com.