An implementation of the Douglas-Peucker algorithm, modified so that the simplified polygon contains the original.
Usage:
rdp_closed(np.array([[0, 0], [-0.1, 1], [0, 2], [4, -1], [0, 0]]), 0.2)
--> [[-0.1 , 0.025],
[-0.1 , 2.075],
[ 4. , -1. ],
[-0.1 , 0.025]]
Notice that usually the new points will not be a subset of the old points, unlike in the original RDP algorithm. However, all the old points will lie on the boundary or interior of the new polygon, and the new polygon will generally be simpler.
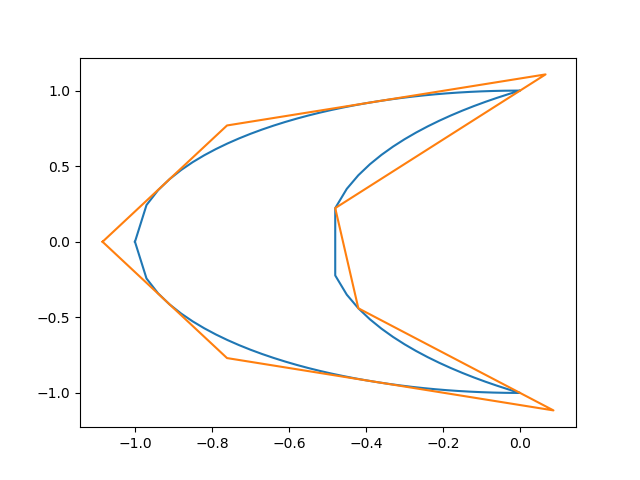
A crescent whose boundary was originally made of two circles, one centered at the origin with radius 1 and the other centered at x=0.75 with radius r=1.25, when simplified with epsilon=0.1, looks like:
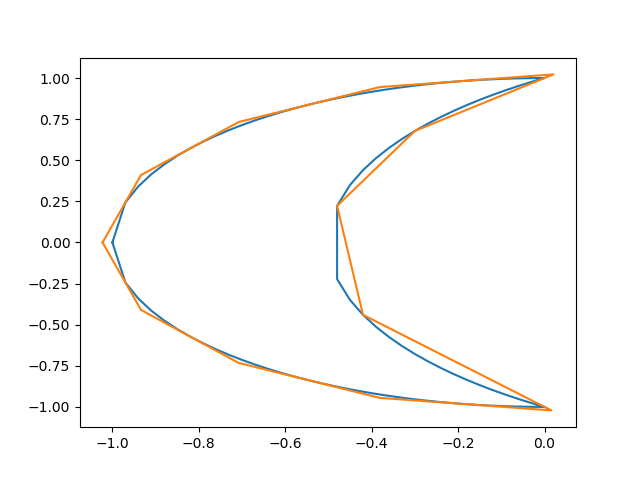
With epsilon=0.05:
Notice how the polygon expands to fit the crescent.