A compilation of books for learning probability and statistics from scratch.
This repository contains an analysis of the commonly recommended books for learning probability and statistics from around the web.
One thing to keep in mind is that advanced mathematics in areas like analysis and measure theory might become more important as we delve deeper into topics. Or may be even before that since things are deeply intertwined all across math. Some of the close adjacent areas to explore after this seems to be information theory, and statistical mechanics/thermodynamics as they can be seen commonly sprucing up in books addressing the topics of probability that I have examined here. I have attempt to put the link to resources directly to those that are freely available and included Amazon affiliate links to others. I have also attempt to link to the places where the resource was recommended from.
TODO: Tag the resources that are free using an icon/tag
The books have been organized into 3 sections, that are ordered as: Introductory → Elementary → Rigorous. The various books I have sampled are categorized into these three sections and within these sections, the books are unordered, which means, I don’t recommend any sequence of reading them inside these broader categories.
Apart from these, as adjuncts, I have also added some history books and topics that are adjacent to probability and statistics one might enjoy learning.
Within the Elementary section, I have tried to categorize the books along 2 axes, { logical, empirical } × { visual, symbolic }.
By a symbolic vs. visual approach, I intend to cover those which take a rigorous algebraic approach vs. ones that lean in on geometric/structural intuition of the concepts at play. These are not mutually exclusive categories and books are situated in a spectrum. With logical vs. empirical approach, I intend to locate those books that have an inclination towards describing the underlying formal patterns as deriving from a rational understanding of the space vs. a more data oriented one where case studies from real world are presented and inferences are inducted from this space. Whenever there was an inclination towards either poles, I have done a rounding off and put it off to align with one of the poles. So even when reading a book classified as say, logical/visual, there is good chance that it will have a good amount of symbolic knowledge to teach you.
For statistics, I have tried to mention whether the books take a frequentist or Bayesian approach with the same caveat of mutual inclusion of ideas as above.
Even though, this is a simplistic division and fails to capture the actual complexity of concepts in probability and statistics, it is the best provisional axes I could supply to make sense of these fields. Once my comprehension of the landscape improves, I will try to adapt/revise the bases to have better span and decomposition properties accordingly.
TODO: May be include a 2 × 2 of the book distribution?
TODO: After listing this out, I have felt that may be a better categorization would be { conceptual, computational } × { probability, statistics }. This would have the books that give a conceptual grounding primarily vs. one that has a lot of exercises to solve which would help the reader arrive at an understanding for the relations at play. Try to do this after you put up the concept lattice for the chapters in the second or third pass.
| Introductory |
|---|
| Probability Theory: First Steps |
| Lady Luck |
| The Lady Tasting Tea |
| The Theory that Would not Die |
| The Art of Statistics |
| Naked Statistics |
| History |
|---|
| Taming of Chance |
| The Empire of Chance |
| The Rise of Statistical Thinking - 1820 – 1900 |
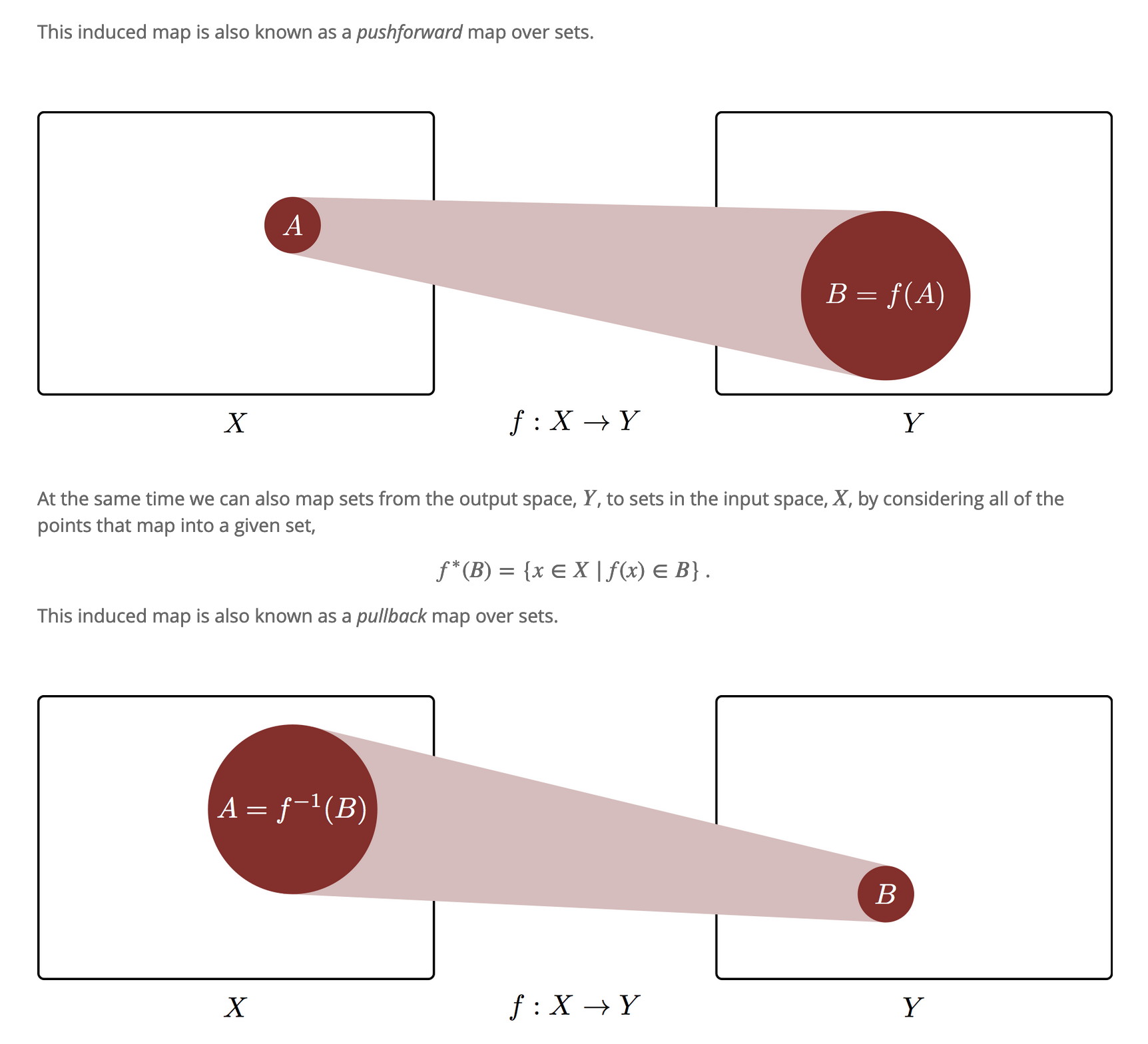
| #chance-logic-and-intuition |
| Additional reads |
|---|
| Against the Gods |
| The (Mis)Behaviour of Markets |
| Information Theory, Inference, and Learning Algorithms |
| Advanced Data Analytics from an Elementary Point of View |
TODO: Add in later by codifying the data on how different books treat different topics.
These are the introductory works into the topic. The books here are popular introductory works into probability which doesn’t get down into the nitty gritty and as such reading these should be supplemented with more rigorous works. They are added here so that an interested reader who is totally new to this domain can build context and familiarize themselves with the central ideas of this field. This also includes some computational notebooks by Peter Norvig which could be of great help in trying to get hands dirty with the algorithms that one uses when trying to navigate the landscape of probability and statistics.

400 pages
An introduction to probability emphasizing the history of the subject.

- April 1, 2001
- 352 pages
Subtitle: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines and Emerged Triumphant from Two Centuries of Controversy

360 pages
A talk based on this book is available here: https://www.youtube.com/watch?v=8oD6eBkjF9o
The book describes the contest between frequentist and Bayesian approaches. It has less mathematics and computation using the mathematical concepts and is rather narrative oriented about how the different ideas panned out.
Subtitle: How to Learn from Data
David Spiegelhalter
2020

An easy introduction into the world of statistics
Charles Wheelan
2014

A narrative driven account of the field of statistics.
Michael Betancourt
October 2018
An online book that provides visual intuition into the ideas of probability along with a good ground work for the mathematical symbolic language that undergirds modern probability theory. The topics are touched upon in a rather cursory manner and might need the support of some other books to thoroughly unravel the underpinnings.
There is also a follow up book from here under Probabilistic Modeling and Statistical Inference

An introduction to probability theory in popular language
Victor Powell
2014
Blog post
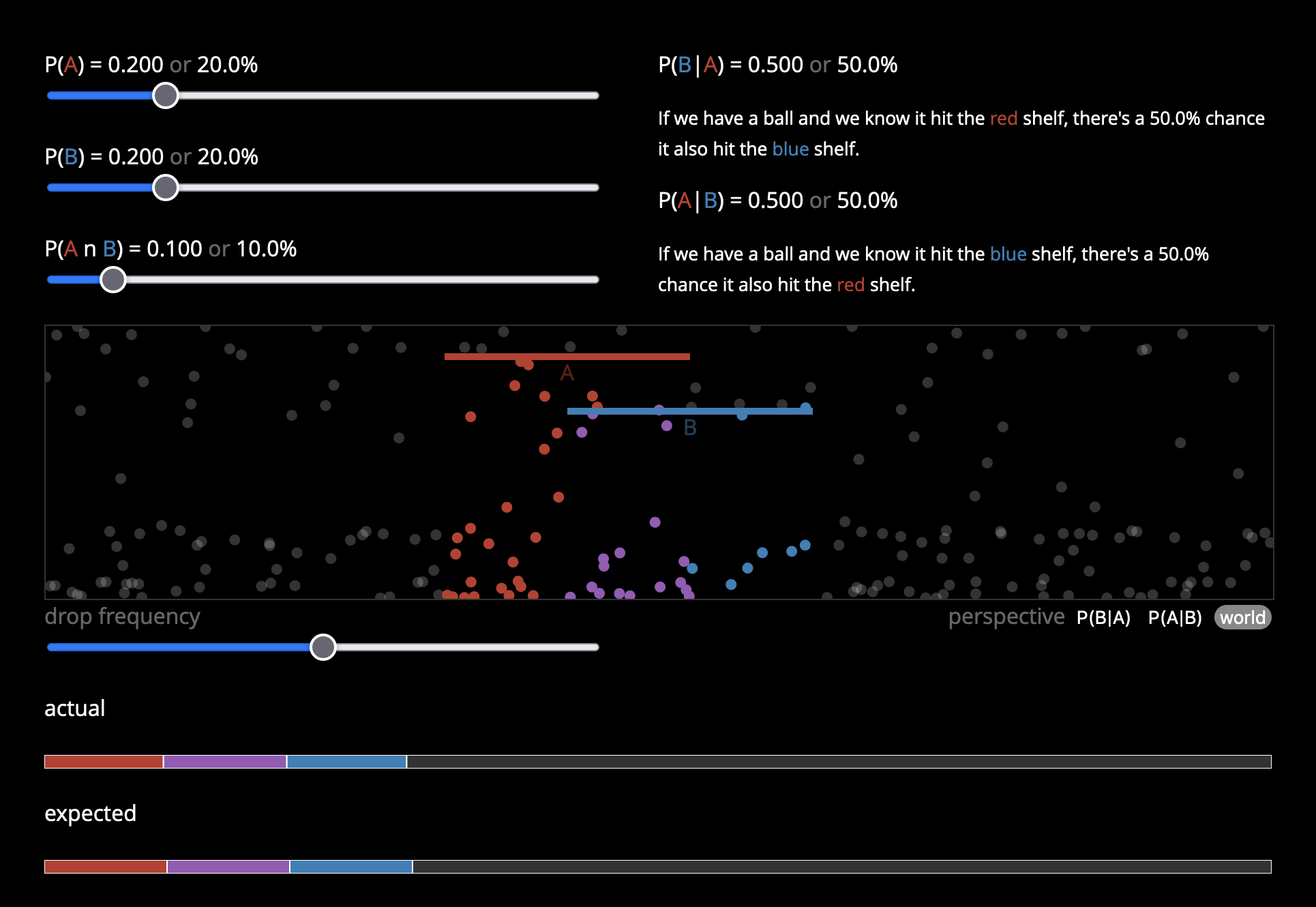
A neat visualization of conditional probability by Victor Powell
These are roughly the works in probability with a symbolic bent or works in statistics with a frequentist approach.

E. T. Jaynes
2003
A Bayesian centric approach on interpreting probability as propositions about reality.
This book was compiled from a posthumous manuscript by the editor Larry Bretthorst.

David Morin
2016
371 pages
A book that attempts to build on the intuition. Less of proving theorems rigorously and there is a combinatorial chapter in the beginning which for building a base in combinatorics.

Dimitri Bertsekas, John Tsitsiklis
June 24, 2002
430 pages
When considering the dimensions between intuition and rigour, this book provides ample intuition to the ideas in probability. It is also supported by some good exercises to work through.

Gian-Carlo Rota, Kenneth Baclawski
An introduction to probability from combinatorialist Rota and data scientist Baclawski based on the lecture notes for the course at MIT. It goes from the elementary concepts of probability and statistics and has a thermodynamics/information theory bend towards the end.

Judea Pearl, Madelyn Glymour, Nicholas P. Jewell
160 pages
2016
Might be a nice book to start reading after The Book of Why to get into some of the nitty gritty on inference from data. There seems also to be a more rigorous work on Causality by Pearl in Causality: Models, Reasoning, and Inference
Hugh Gordon
2012

A book explaining discrete probability in an accessible language.
These are roughly the works with a Bayesian / Data centric bent which focusses on a symbolic approach. The more rigorous works in studies can also be seen in this section as visual ideas haven’t matured to capture the rigorous nature of mathematical machinery employed to make sense of the ideas in this field.
Dennis V. Lindley
1st Edition (2006)

An introductory book that gives a conceptual grounding for the ideas in probability and statistics.
Peter Whittle
1992

Frequentist introduction to probability that takes an abstract approach.
David R. Cox
2006

Frequentist introduction to statistical inference giving a comparison of various approaches.

Larry Wasserman
An introductory book that takes a rigorous approach towards introducing the concepts. Might not be the most apt book to start for learning statistics from scratch, but once you are confident about the basics, this is highly recommended as a book to learn the elements of statistics.
Bruno de Finetti
1974

A Bayesian approach on probability as accounting for consequences of decisions made.
Subtitle: A Bayesian course with examples in R and STAN
Richard McElreath
2020
A computational approach to Bayesian statistics. Not theoretically demanding as Gelman’s Bayesian Data Analysis, and helps a mathematical novice to see their way around the computational processes underpinning Bayesian statistics.
Allen B. Downey
2011

A book that teaches statistics by programming through Python
David Diez, Mike Çetinkaya-Rundel, Christopher Barr
2019

An open source text book for learning statistics along with supporting video lectures and labs.
Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani
2013

Less background required than The Elements of Statistical Learning
Subtitle: Data Mining, Inference, Prediction
Trevor Hastie, Robert Tibshirani, Jerome Friedman
1st published: 2001, 2nd Edition: 2009

A thorough book giving sound overview of the fundamentals of statistics.

David Freedman, Robert Pisani, Roger Purves
4th Edition (2007)
A book directed towards people with minimal mathematics exposure. The organization of the book in helping build the intuition gradually is remarked by people have read it.
Sheldon Ross
First Edition: 1987, 6th Edition: 2020

Used as a common textbook in many universities.
Charles M. Grinstead, J. Laurie Snell
1997
528 pages

An open source text book to learn probability that takes a calculus based approach instead of combinatorial one.
Morris DeGroot, Mark Schervish
First Edition: 1975, Fourth Edition: 2013

A highly recommended book for learning both probability and statistics.
Allen Downey

2012
An introduction to Bayesian probability in the style of Think Stats
Henk Tijms
2012
574 pages

The book is divide into two parts with the first part giving an intuition for the concepts involved and the second giving the subject a more formal treatment.
Joseph K. Blitzstein, Jessica Hwang
1st Edition: 2014, 2nd Edition: 2019

A highly recommended book to learn probability from. Comes with an accompanying MOOC: https://projects.iq.harvard.edu/stat110/home
These are roughly the works with a Bayesian / Data centric bent which focusses on a visual approach.

Lev Tarasov (Translated by Michael Burov)
1984
198 pages
An introduction to the subject of probability motivated by examples from decision making, control theory, biology, and quantum mechanics. Was originally published in Russian and translated to English.
There are some really well written computational notebooks by Peter Norvig elucidating the probabilty concepts.
TODO: Add images for each of the Python notebooks
Dan Morris
114 pages

A short and quick introduction to Bayes Theorem.
Daniel Kunin, Jingru Guo, Tyler Dae Devlin, Daniel Xiang
An interactive website introducing the concepts of probability and statistics.
An overview of the history would benefit by providing the motivation and original scenarios in which the concepts originated. They are also a good way for people looking to research into this area to understand some of the original strands and possible find a wealth of problems that are linked with the genesis of the ideas.
Ian Hacking
1990

A standard recommendation to learn about the origins of probability ad statistics. This book, along with The Emergence of Probability by Hacking, which has a more philosophical bent, might serve as a decent bundle for exposure to the historical details on how probability took shape as a science.

Gerd Gigerenzer, Zeno Swijtink, Theodore Porter, Lorraine Daston, John Beatty, Lorenz Krüger
October 26, 1990
360 pages
History of modern statistics and its connections with other domains of knowledge.
Theodore M. Porter
August 18, 2020
360 pages

History of the subject with more of an academic bent. A general reader might find Ian Hacking’s work more approachable.
I. Todhunter
1865
Steven Tjims
18 February 2021 256 pages
TODO: Add link and brief
https://www.youtube.com/playlist?list=PL17567A1A3F5DB5E4
Paul G. Hoel, Sidney C. Port, Charles J. Stone
1972
They also have a similar book on Statistical Theory.
A rigorous introduction to probability theory. It has been likened to Rudin’s book on mathematical analysis.
Patrick Billingsley
2012
A self-contained book on probability and commonly recommended as a rigorous introduction to the subject.
Jim Pitman
Kai Lai Chung
Sidney Resnick
Krishna B. Athreya, Soumendra N. Lahiri
Andrew Gelman, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, Donald B. Rubin
First Edition: 1995, Second Edition: 2003, Third Edition: 2013
David Williams
Rick Durrett
Leonard J. Savage
Oliver Knill
Bradley Efron, Trevor Hastie
George Casella and Roger Berger
Typically used in many universities as the starting text. Apparently more rigorous and more focused on technical details than All of Statistics.
William Feller
Achim Klenke
Recommended as a reference book on probability
Geoffrey R. Grimmett, David R. Stirzaker
Considered a standard reference to the subject
Andrew Gelman, Jennifer Hill
2006
Peter L. Bernstein 1998
Benoit B. Mandelbrot, Richard L Hudson
David MacKay If you want to have an Information Theory bend
Cosma Rohilla Chalizi
Kaisa Taipale
An idiosyncratic tour through ideas in probability, calculus, linear algebra, and statistics
Edward Nelson
The book has an econometric viewpoint towards how to infer cause and effect using statistics.
Anthony Hayter
Noga Alon and Joel H. Spencer
Robert L. Waldrop
Jim Frost
Michael Franke