Slitherlinky is a solver for slitherlink puzzles. Slitherlinky reduces a puzzle to a SAT problem, which is then solved by a SAT solver.
Slitherlink, also called Loop the Loop (and a plethora of other names all over the world) is a logic puzzle. You can read more about it on Wikipedia. Because it appears in the most popular English newspaper in India, it is quite popular amongst Indians.
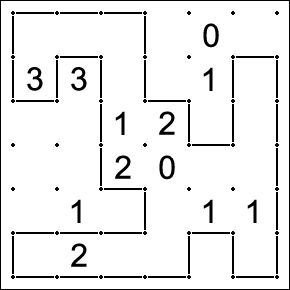
Slitherlink is played on a rectangular lattice of dots. Some of the squares formed by the dots have numbers inside them. The objective is to connect horizontally and vertically adjacent dots so that the lines form a simple loop with no loose ends. In addition, the number inside a square represents how many of its four sides are segments in the loop.
There are three constraints in Slitherlink that need to be expressed to the SAT solver. The choice of boolean variables is also decided accordingly.
-
Cell Imposed Constraints: This is the obvious one. Every cell with a number inside should have equivalent number of edges.
-
Loop Constraints: Every corner should be part of either 0 or 2 edges. This is sufficient to ensure that edges form a loop.
-
Single Loop Constraints: The above two conditions do not restrict multiple loops from being formed. For that, we would require a predicate variable for connected relation which is a transitive closure of the adjacency relation for edges.
There are two kinds of variables that are needed to express this problem.
-
Edge Variables: Every possible edge is represented by a boolean. If the variable is true in a satisfiable solution, then there is an edge in that position. Edge variables are sufficient to express the Cell Imposed Constraints as well as the Loop Constraints. In an n * n grid (the example above is a 6 x 6 grid), there are 2n(n + 1) edge variables. Notation: e(i) represents the edge i.
-
Connected Variables: There are E * E such variables, where E is the number of edges. Notation c(i, j) represents that e(i) and e(j) are connected. These variables are required to express the Single Loop Constraints described above.
- If e(i) and e(j) correspond to adjacent edges, then
e(i) AND e(j) <=> c(i, j) - If they are not adjacent, then we need to express this recursively. Assume
that the k1, k2 ... are the neighbours of edge i.
e(i) AND e(j) AND ((e(k1) AND c(k1, j)) OR (e(k2) AND c(k2, j)) OR ..) <=> c(i, j)
- If e(i) and e(j) correspond to adjacent edges, then
Slitherlink is written in Python3. It also requires a pycosat, a SAT solver. pycosat can be installed using pip or conda.
pip install pycosat
conda install pycosat
The test problems can be found in the tests/ directory.
python3 slitherlinky.py -f tests/55easy1.txt
python3 slitherlinky.py -f tests/55easy2.txt
python3 slitherlinky.py -f tests/55hard1.txt
python3 slitherlinky.py -f tests/55hard2.txt
I wrote this to kill boredom on a dull Saturday. I live here on the internet.
This project is licensed under the MIT License - see the LICENSE.md file for details